Operating sysetem - CPU_scheduling
◼︎ 워크로드에 대한 가정
- 워크로드(work load): 일련의 프로세스들이 실행하는 상황
우리는 시스템에서 실행 중인 프로세스 혹은 작업에 대해 다음과 같은 가정을 한다.- 모든 작업은 같은 시간 동안 실행
- 모든 작업 동시에 도착
- 각 작업은 시작되면 완료될 때까지 실행
- 모든 작업은 CPU만 사용 (입출력을 수행하지 않는다.)
- 각 작업의 실행 시간은 사전에 알려져 있다
◼︎ 스케줄링 평가 항목
이렇게 가정된 워크로드로 만든 스케줄링이 있을 것이다. 그런데 이 스케줄링중 어떤게 더 좋은지 평가하는 기준이 필요할 것이다. 그래서 우리는 스케줄링 평가 항목(scheduling metric)을 결정해야 한다. 이 평가 기준은 여러개가 존재한다.
반환 시간(turnaround time)
- $T_{turnaround}$ : 반환 시간
- $T_{completion}$ : 종료 시간(마지막 것이 도착한 시간)
- $T_{arrival}$ : 도착 시간(맨 처음 도착한 시간)
반환 시간은 이렇게 정의되었지만 위에서 가정했듯이 모든 작업은 동시에 도착한다. 그렇기 때문에 $T_{arrival} = 0$이 되어 $T_{turnaround} = T_{completion}$이다.
반환 시간은 성능을 중점으로 둔 평가기준이다. 성능 이외의 평가 기준으로는 공정성(fairness)가 있다. 성능과 공정성은 서로 상충된다.
◼︎ FIFO (선입선출)
가장 기초적인 알고리즘은 선입선출(First In First Out, FIFO)와 선도착선처리(First Come First Served, FCFS)이다.
FIFO의 장점
- 단순하다
- 구현하기 쉽다
- 가정 하에서 매우 잘 작동한다
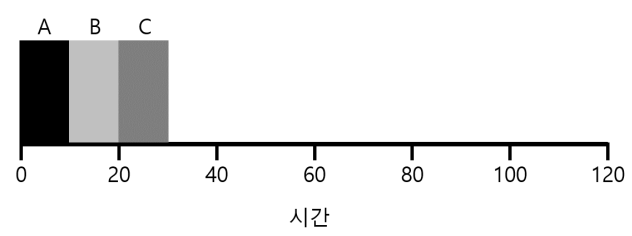
작업 3개가 거의 동시에 A, B, C 순서대로 도착했다고 가정햇을 때 세 작업의 평균 반환 시간은 $\frac{10+20+30}{3} = 20$이다.
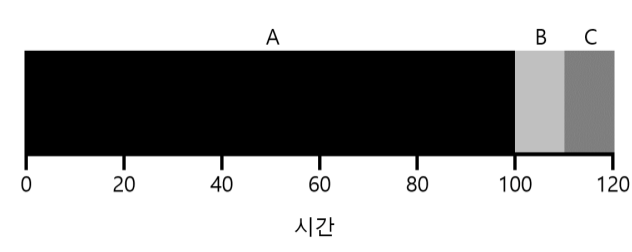
세 작업의 평균 반환 시간은 $\frac{100+110+120}{3} = 110$이다. 이렇게 굉장히 비효율적인 평균 반환 시간을 보여준다. 이것은 FIFO가 그렇게 좋은 스케줄링이 아닌 이유이다. 이 문제점을 convoy effect라고 한다.
SJF (최단 작업 우선)
위의 문제를 해결하기 위해서 최단 작업 우선(Shortest Job First, SJF)방식을 사용한다. 이 방식은 *비선점(non-preemptive)** 스케줄러이다.
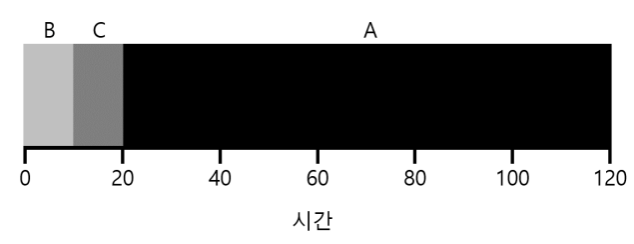
세 작업의 평균 반환 시간은 $\frac{10+20+120}{3} = 50$이다. 위에서 계속 그러했듯이 모든 작업이 동시에 도착한다면 무조건 SJF가 최적의 스케줄링 알고리즘이다. 하지만 이 가정은 비현실적이다. 만약 모든 작업이 동시에 도착하는 것이 아니다고하면 어떻게 해야할까?
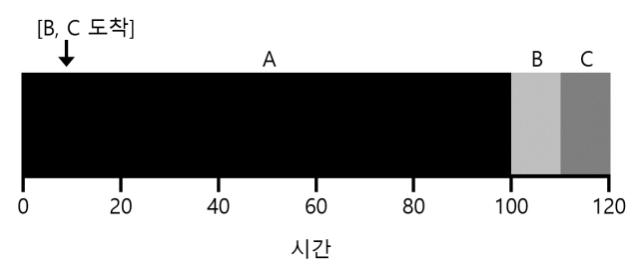
세 작업의 평균 반환 시간은 $\frac{100+(110-10)+(120-10)}{3} = 103.33$이다.
STCF (최소 잔여시간 우선)
위의 문제를 해결하기 위해서는 가정 3을 완화해야한다. 작업 도중 다른 작업을 하고 다시 돌아올 수 있다. 이렇게 선점기능을 추가한 최단 잔여시간 우선(Shortest Time-to-Completion First, STCF)방식이 있다.
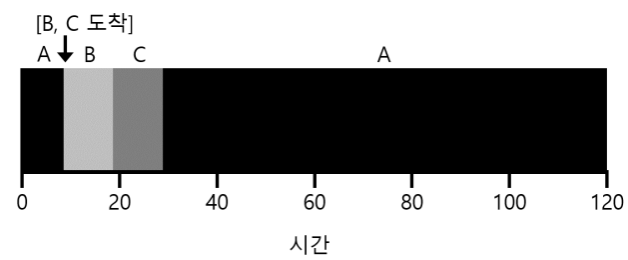
세 작업의 평균 반환 시간은 $\frac{120+(20-10)+(30-10)}{3} = 50$이다.
새로운 평가 기준: 응답 시간
작업이 CPU만 사용하고 평가 기준이 반환 시간만 봤을 때는 CTCF는 굉장히 효율적인 알고리즘이었다. 그래서 초기 일괄처리 컴퓨터 시스템에서는 좋았다. 하지만 시분할 컴퓨터의 등장으로 이것이 더 이상 효율적이지 않게 되었다.
응답 시간
- $T_{response}$ : 응답 시간(response time)
- $T_{firstrun}$ : 프로세스가 처음 실행되는 시간
- $T_{arrival}$ : 도착 시간(맨 처음 도착한 시간)
작업의 앞부분의 시간을 보면 된다.
A는 0에서 B, C는 10일때 도착할 경우 위 예시의 평균 작업 시간은 $\frac{0 + 0 + 10}{3} = 3.33$
RR(라운드 로빈)
이 응답 시간 문제를 해결하기 위해 라운드 로빈(Round-Robin, RR)스케줄링 방식을 사용한다. 작업이 끝날 때 까지 기다리는 것이 아니라 일정 시간 동안 실행하고 다음 작업으로 전환을 하는 것이다. 이 때 작업이 실행되는 일정한 시간을 타임 슬라이스(time slice) 또는 스케줄링 퀀텀(scheduling quantum)이라고 한다. 그래서 RR은 타임 슬라이싱이라고도 불린다.
타임 슬라이스의 길이는 무조건 타이머 인터럽트 주기의 배수여야한다.
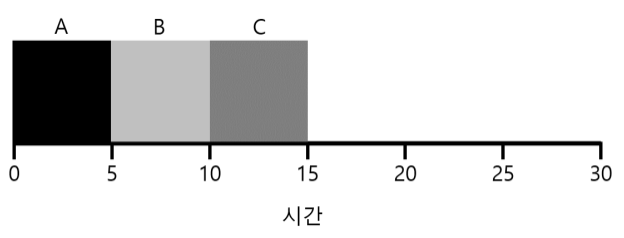
위의 그림같은 경우 SJF방식인데 이의 평균 응답 시간은 $\frac{0+5+10}{3} = 5$이다.
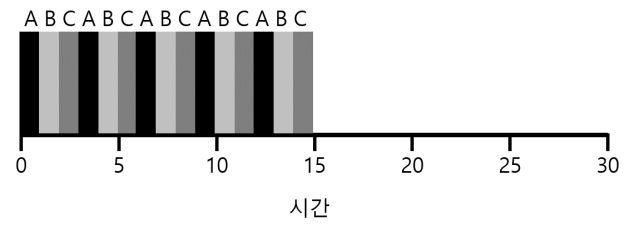
위는 RR을 적용한 스케줄러이다. 평균 응답 시간은 $\frac{0+1+2}{3} = 1$이다.
이렇게 응답 시간은 타임 슬라이스가 짧을수록 RR의 성능은 좋아진다. 하지만 너무 짧게 지정하면 문맥 교환 비용이 너무 크게 들어 전체 성능에 영향을 미치게 된다.
비용의 상쇄
상쇄(amortization)은 어떤 연산에 고정 비용이 존재하는 시스템에서 사용된다. 그 고정비용이 적은 횟수로 발생시키면 시스템의 전체 비용이 감소된다. 10번에 1번씩 낼 비용을 100번에 1번씩 내게 하는 것이다.

반환 시간은?
위의 RR스케줄러 반환 시간은 $\frac{13 + 14 + 15}{3} = 14$로 별로 좋지 않은 반환 시간을 가진다. 이렇게 서로의 평가 기준이 상충되게 된다. 반환 시간은 성능을 우선시하는 평가 기준이고 응답시간은 공정성을 우선시하는 평가 기준이다.
◼︎ 입출력 연산의 고려
아직 완화하지 않은 조건인 4번을 완화해볼 것이다. 이제 입출력을 할 것이다. 우선 입출력 작업을 요청한 경우 스케줄러가어떤 작업을 하는지 알아야 한다. 입출력 작업을 완료 할때까지 CPU는 사용되지 않게된다.
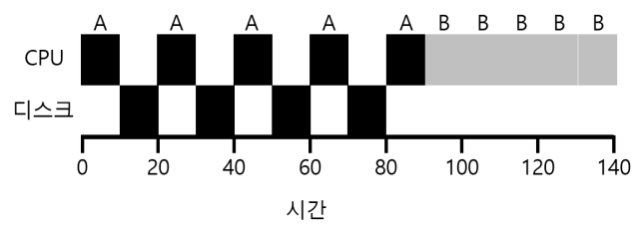
A, B 작업 모두 CPU에서 50만큼의 시간을 필요로 하고 A는 10마다 입출력 요청을 하고 B는 입출력을 수행하지 않는다. 그러면 위의 그림처럼 비효율적이게 하게 된다.
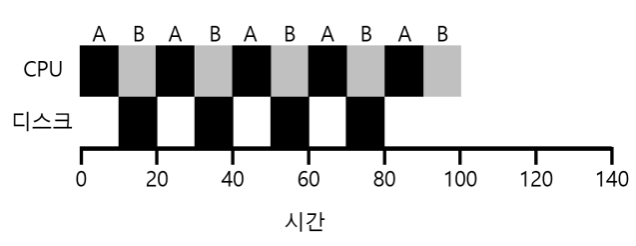
CTCF방식을 이용해 중첩을 하면 훨신 더 효율적인 스케줄러를 만들 수 있다.
만능은 없다
아직까지 마지막 가정을 완화하지 않았다. 그런데 사실 각 작업의 실행 시간을 알고 있는다는 것은 불가능 하다. 그렇기 때문에 완벽한 알고리즘을 찾기는 불가능하다. 하지만 그래도 가까운 과거를 이용하여 미래를 예측하는 스케줄러를 구현할 것이다. 이것은 멀티 레벨 피드백 큐(multi-level feedback queue)라고 한다.