6 minute read

이제 좀 다른 이야기를 해 볼것이다. 방금 전까지 우리는 연속적인(continuous)한 output에 대해 다뤘는데 이제는 불연속(discrete)한 output인 경우에 대해 알아볼 것이다. Classifier라는 것을 다룰 것인데 이것은 logistic regression이라는 것을 이용하는 것이다. 일단 classify에서 눈치를 챌 수 있듯 뭔가 분류되고 그런것에 대한 이야기이다.

◼︎ Classifier application

무엇인가 분류하는데는 여러가지 상황들이 있을 것이다. 그중 spam mail을 filtering하는 모델을 만든다고 하자. 그러면 input으로는 text, IP, 보낸사람 이름 등 여러 feature가 있을 것이다. 그리고 output으로는 spam메일이거나 spam메일이 아니거나 이렇게 두 개가 있을 것이다. 근데 output이 두 개 이상인 상황도 있을 수 있지 않을까? 이것을 multiclass classifier라고 한다.

◼︎ Linear classifiers

일단 봤던 그림이겠지만 이 그림을 계속 기억해 두자.

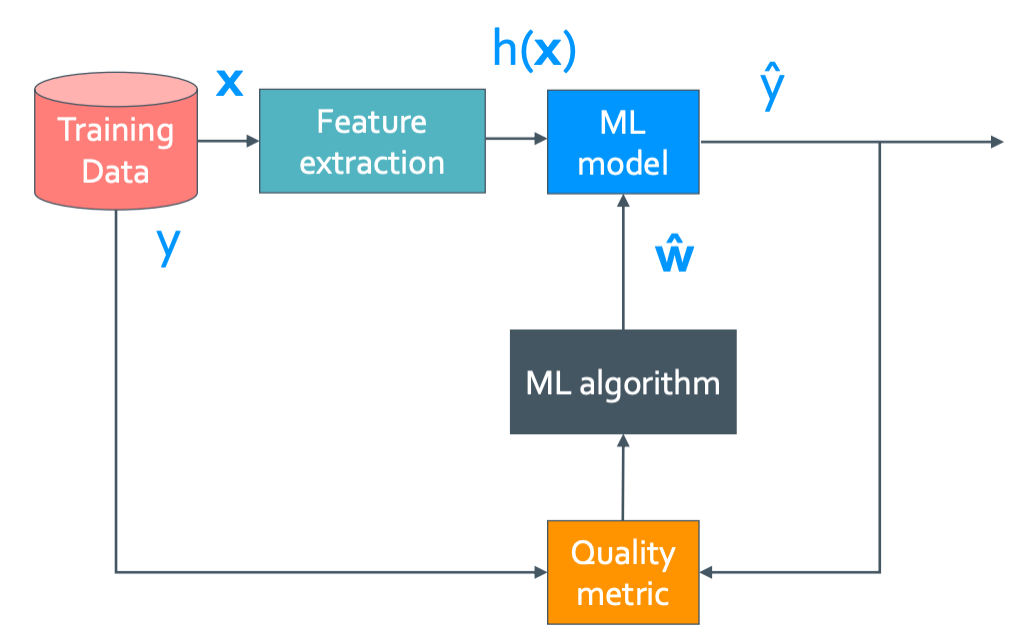
이 그림에서 윗부분인 ML model만들기를 해 볼것이다. 예시로는 음식점을 평가하는 model을 만드는 과정을 보여줄 것이다.

Input으로는 사람들이 쓴 음식점에 대한 리뷰를 넣을 것이고 맛있는 음식점이면 output으로 +1을 맛 없으면 -1을 내보낼 것이다. 그러면 이 평가 모델은 어떻게 구성해야 할까?

1
2
3
4
5
6
7
8
9

# Simple threshold classifier

count_p = positive_word_in_sentence
count_n = negative_word_in_sentence

if (count_p > count_n)
    y = +1
else
    y = -1

이렇게 단순한 평가 모델을 구성할 수 있을 것이다. 그런데 이 classifier에는 문제가 있다.

  1. positive/negative word를 어떤 기준으로 나눌 수 있는 것일까?
  2. 그 표현들에는 정도의 차이도 있지 않나? 맛있다와 ㅈㄴ맛있다를 같은 급으로 두면 안될것 같은데….
  3. 맛있다를 positive으로 뒀는데 만약 평가에 맛있지 않다라고 써두면 postive라고 읽을 수도 있을것 같은데?

1번과 2번의 문제는 classifier를 학습 시키면서 해결할 것이고 3번째 문제는 더 feature를 정교하게(elaborate)만들어서 해결할 것이다.

A linear classifier

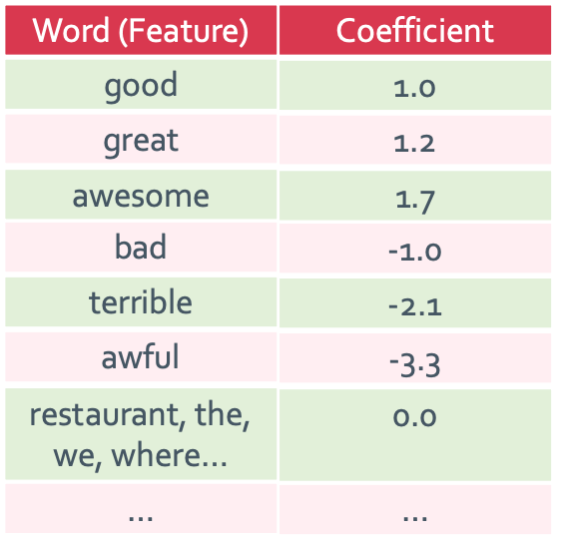
이렇게 coefficient를 만드는데 이 숫자조차도 data들로 학습을 할 것이다. 그럼 위에서 만든 모델을 다음과 같이 좀 수정할 수 있을 것이다.

1
2
3
4
5
6
7
8

# Modified simple threshold classifier

score(x) = weighted_sum_of_features_of_sentence

if (score(x)>0)
    y = +1
else
    y = -1

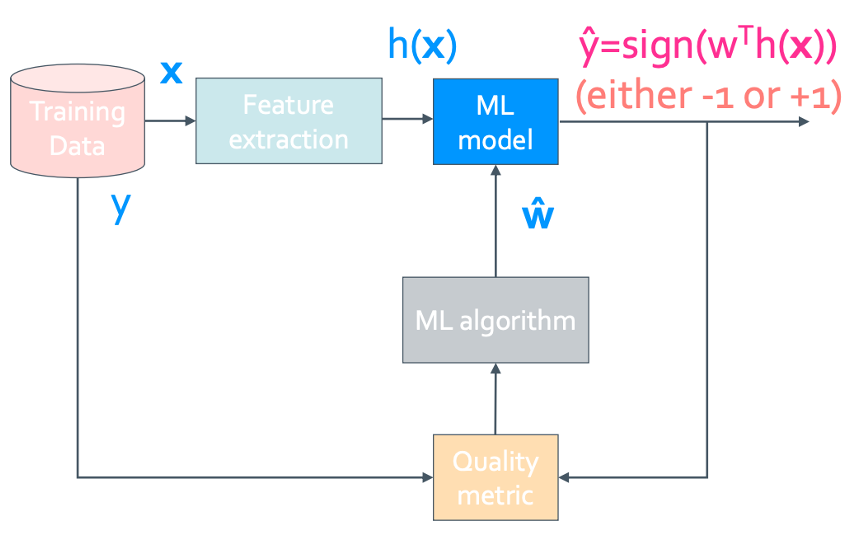
양수가 나오면 +1로 음수이면 -1로 만드는 알고리즘으로 짠 것이다. 좀 더 수학적으로 표현한 것은 다음과 같다.

Model: $\hat{y} =$ sign(Score($x_i$))
where, sign(x)= $\begin{cases} +1 & x \leq 0 \newline -1 & x < 0 \end{cases}$

Score($x_i$)= $w_0h_0(x_i)+w_1h_1(x_i)+...+w_Dh_D(x_i)$
$= \sum_{j=0}^{D}w_jh_j(x_i)=w^Th(x_i)$

이것을 위에서 본 ML model에서 보면 다음과 같다.



◼︎ Decision boundaries

일단 w의 개수를 많이 늘리지 말고 딱 3개만 있는 경우로 생각해보자. 일단 단어(coefficient)에는 #awesome과 #awful만 있다고 하고 나머지는 value가 0인 $w_0$가 있을 때 각 feature들에 각각 #awesome과 #awful 세어서 그래프에 나타내보자.

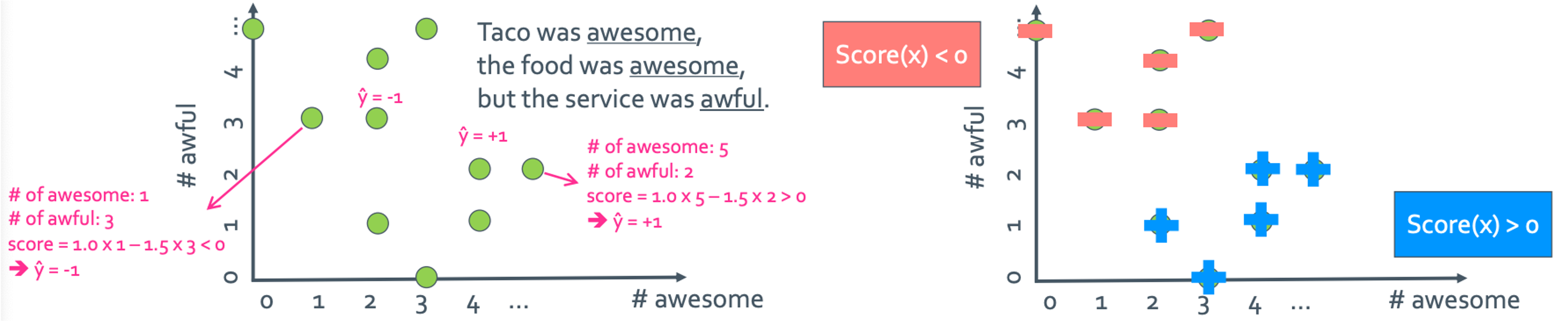
이렇게 찍은 점들에다가 양의 값인지 음의 값인지를 표시하면 오른쪽의 표처럼 그려진다. 그러면 뭔가 보이지 않는 선에 의해 +와 -가 갈라져있는 것처럼 보이지 않나?

진짜로 선을 그으면 다음과 같고 w요소를 하나 더 늘리면 이렇게 3차원 공간에 평면으로 boundary가 생길 것이다. 그런데 꼭 이렇게 직선적으로만 될 필요는 없다.

Polynomial feature

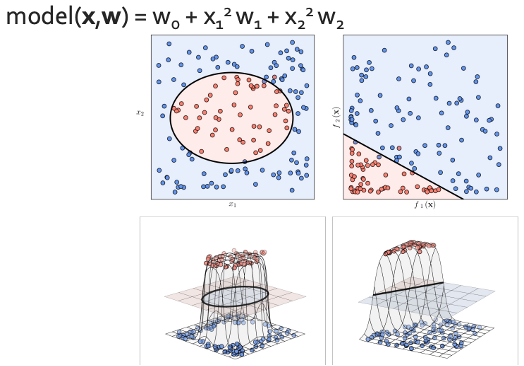
이렇게 polynomial하게 나눠도 무방하다.

Feature transform

이렇게 극변환을 해도 되고 수업때 말한 것인데 그냥 이상태에서 z축을 추가해 +인것은 0의 z축에 두고 -인것은 높이를 만들어 줘도 된다. 되게 많이 사용하는 방식이라고 했다.

◼︎ Class probability

이렇게 모델을 열심히 만들었는데 과연 이 모델이 신뢰할 수 있을지는 다른문제이다. 그래서 이것을 확률을 이용해 알아볼 것이다.

Using probabilities in classification

이 질문에 대해 생각을 해 봐야한다. “얼마나 그 예측이 맞는 확신해?”

3000만큼

조금 더 정량적으로 해서 “그 예측이 맞다고 몇 퍼센트 확신해?”

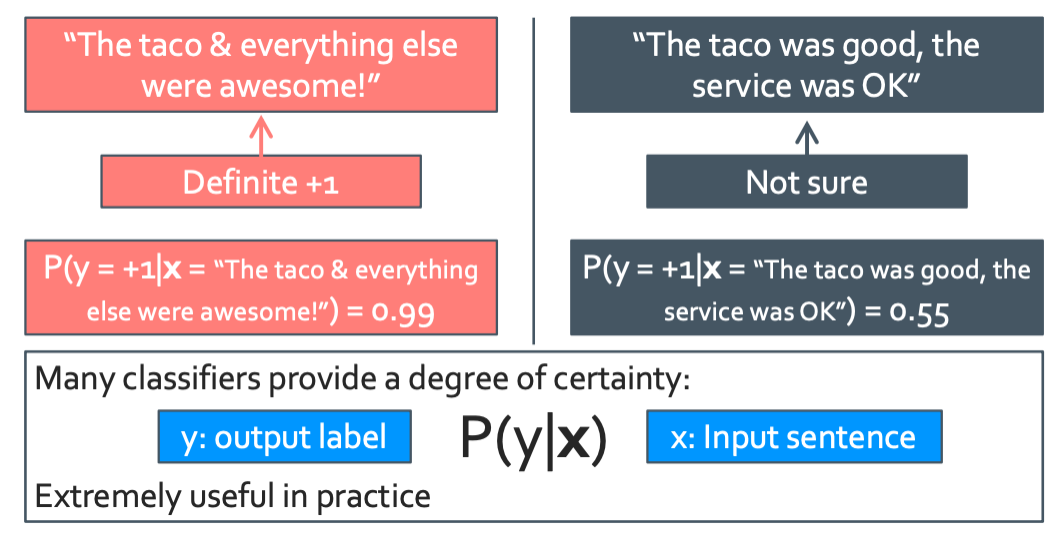
이렇게 신뢰도를 확률로 둘 수 있을 것이다. 이를 토대로 또 알고리즘을 만들어보자.

1
2
3
4
5
6
7
8

# Predict most likely class

P(y|x) = estimate_of_class_probabilities

if (P(y=+1|x)>0.5)
    y = +1
else
    y = -1

이렇게 두는 것의 장점은 두 가지 내용을 다 판단할 수 있다는 것이다. 0.5보다 크다는 것은 신뢰할만 하다는 것이니까 맛있다는 것이고 0.5 이하는 신뢰하지 못하므로 맛없다는 것을 알 수 있다. 그 중에서도 숫자가 얼마나 큰지를 통해 진짜 맛있는지 그냥 저냥 맛있는지도 판단할 수 있다.
결과적으로 imporves interpretability

◼︎ Logistic regression

그래서 우리는 두 가지의 평가 알고리즘을 만들었다. Score($x_i$)와 $\hat{H}(y=\,+1|x, \hat{w})$ 이 알고리즘들을 어떻게 연결시켜줘야할까? 두 개를 합칠 수 있으면 좋을것 같다.

Sigmoid

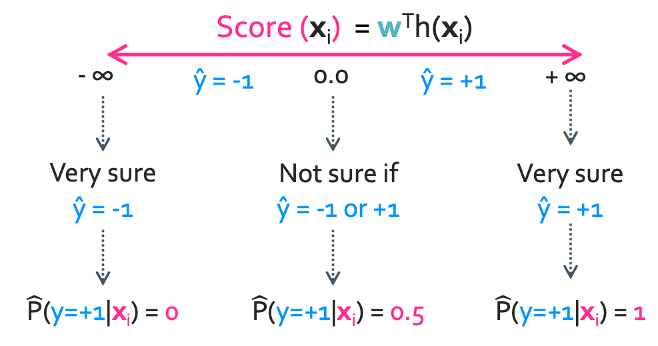
이렇게 대응시키면 어떨까? ($-\infty$ → 0, 0 → 0.5, $\infty$ → 1)
이렇게 축소시키려면 어떤 함수에 넣어야할까? 이걸 해결하기 위해 도입하는 함수가 sigmoid함수이다.

$\operatorname{Sigmoid}(\mathsf{Score}) = \frac{1}{1+e^{-\mathsf{Score}}}$

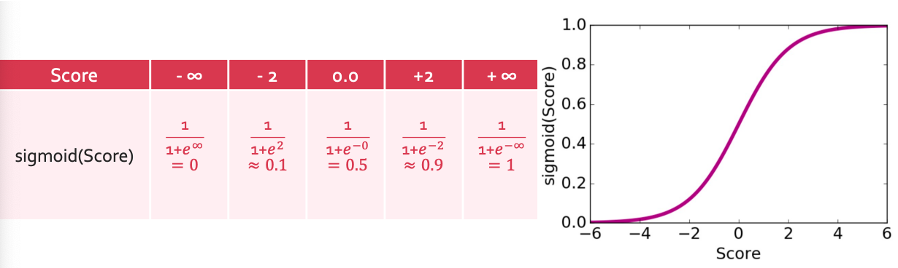
Odds

Probability는 우리가 아는 그 확률인데 odds는 무었일까? odd는 일어나는 사건과 일어나지 않는 사건의 비율이라 생각하면 된다.

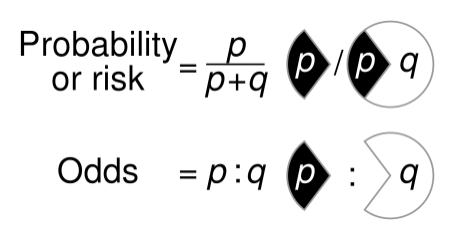
그래서 만약 +1과 -1로만 나눠지는 사건 두 개가 있다고 할때 이 사건의 probability와 odds는

logit = logistic + unit= log-odds

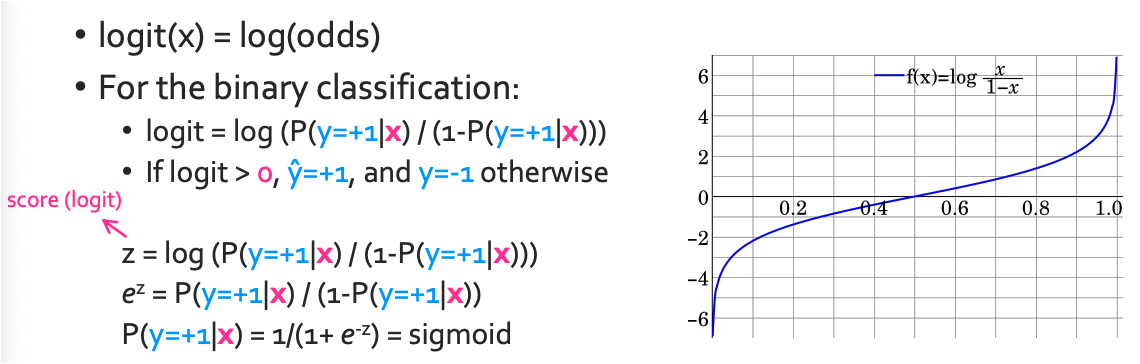
그래서 ML에서 보통 score는 그냥 logits이라고 불리고 sigmoid function과 inverse관계이다.
최종적으로 구한 식은 다음과 같을 것이다.

$\mathsf{P}(y= \,+1|x_i,w) = \operatorname{Sigmoid}(\mathsf{Score}(x_i)) = \frac{1}{1+e^{-w^Th(x)}}$


◼︎ Quality metric for logistic regression: Maximum likelihood estimation

위에서 언급했는데 단어들의 coefficient가 갖는 값들도 training을 통해 learninig시킨다고 했다. 이것을 하는 방법을 이제 알아볼 것이다.

이렇게 확률들을 곱 $l(w)$를 두고 제일 클 때 제일 좋은 모델이라고 할 수 있지 않을까? 이 최대값은 어떻게 찾을까? 익숙한 방법을 이용해 볼것이다.

◼︎ Gradient axcent for logistic regression

일단 많이 했봤듯이 $\triangledown l(w)=0$은 안되는 것을 알고 있을 것이다. 그래서 지금 최소값을 찾는게 아니라 최대값을 찾아야하니 gradient descent가 아닌 gradient ascent를 한다.

계산을 위해 이렇게 log를 씌워주었다.

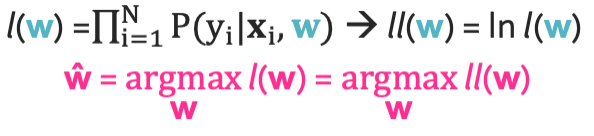
Step 1: Rewrite log_likelihood

일단 indicator function에 대해 알아야한다.

Indicator function:
$ \mathit{1}[y_i= \,+1]= \begin{cases} 1 & y_i = \,+1\newline 0 & y_i = \,-1 \end{cases}$

$ \mathit{1}[y_i= \,-1]= 1 - \mathit{1}[y_i= \,+1]\begin{cases} 1 & y_i = \,-1\newline 0 & y_i = \,+1 \end{cases}$

이 indicator function을 이용하면 식을 이렇게 바꿀 수 있다.

$ll(w) = \sum_{i=1}^{N} ln \mathsf{P}(y_i|x_i,w)$


$= \sum_{i=1}^{N} [\mathit{1}[y_i= \,+1]\,ln \mathsf{P}(y_i= \,+1|x_i,w)+\mathit{1}[y_i= \,-1]\,ln \mathsf{P}(y_i= \,-1|x_i,w)]$

Step 2: Express probabilities in terms of w and h(x)

  • y = +1의 probability
    $\mathsf{P}(y= \,+1|x,w) = \frac{1}{1+e^{-w^Th(x)}}$
  • y = -1의 probability
    $\mathsf{P}(y= \,-1|x,w) = \frac{e^{-w^Th(x)}}{1+e^{-w^Th(x)}}$

Step 3: Plugging in for 1 data point

대입하면 된다.

$= \sum_{i=1}^{N} [\mathit{1}[y_i= \,+1]\,ln \mathsf{P}(y_i= \,+1|x_i,w)+\mathit{1}[y_i= \,-1]\,ln \mathsf{P}(y_i= \,-1|x_i,w)]$


$= (1 - \mathit{1}[y_i= \,+1])(-w^Th(x))-ln(1+e^{-w^Th(x)})$


Step 4: Gradient for 1 data point

$\frac{\partial ll(w)}{\partial w_j}= -(1 - \mathit{1}[y_i= \,+1])h_j(x_i) + \frac{e^{-w^Th_j(x_i)}}{1+e^{-w^Th(x_i)}}h_j(x_i)$


$= (\mathit{1}[y_i= \,+1] - \mathsf{P}(y= \,+1|x,w))h_j(x_i)$
$(\because \frac{e^{-w^Th_j(x_i)}}{1+e^{-w^Th(x_i)}}h_j(x_i) = \mathsf{P}(y= \,-1|x,w))$


Step 5: Gradient over all data points

Finally

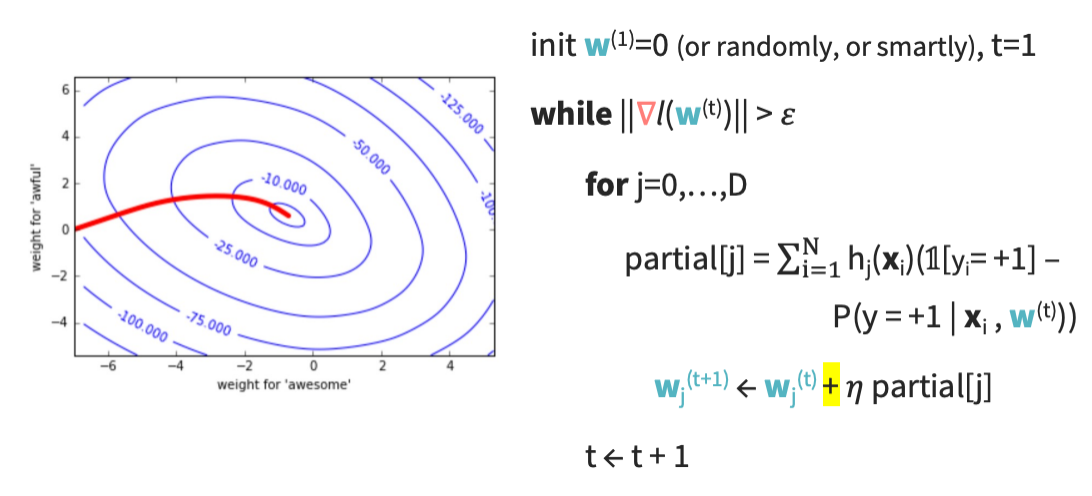
이렇게 구한 gradient를 ascent니 +로 넣어주면 된다.

◼︎ Quality metric for logistic regression: Cost function

우리는 cost function을 J라고 쓰고 cross entropy loss라고도 한다. 식으로 쓰면 다음과 같다.

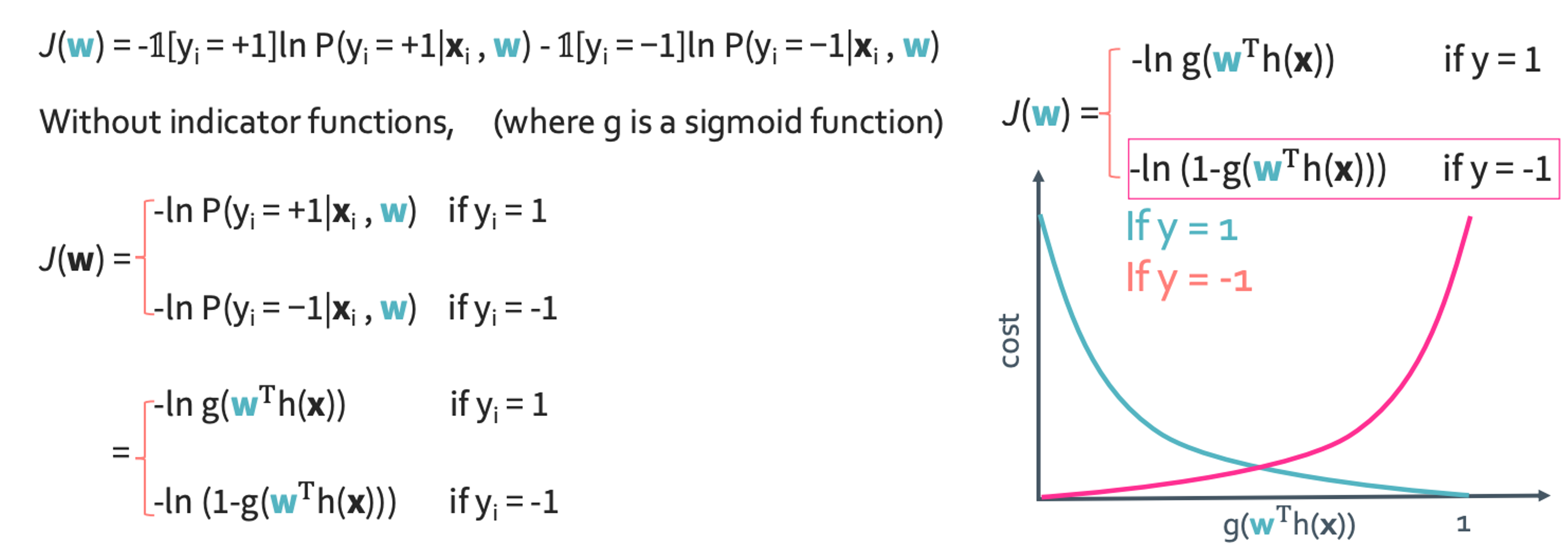
이것을 그래프로 그리면 위와 같이 된다.

◼︎ Entropy, cross entropy and KL divergence

Information content(정보량)

정보량은 잘 일어나지 않을수록 정보량이 많게 된다. E를 사건 P(E)를 사건이 일어날 확률이라고 하자. 그러면 정보량을 수치화하면

$I(E) = -log(P(E))$

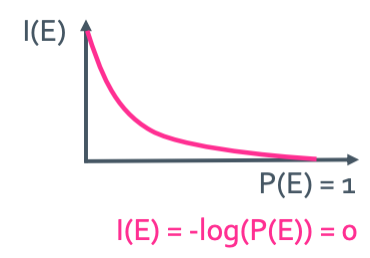
라고 할 수 있을 것이다.

Entropy

엔트로피란 정보를 표현하는데 필요한 최소 평균 자원량이다. 예를 들어 무지개를 LED 하나 하나로 만든다고 하면 7개의 LED필요할 것이다. 이 LED를 verilog를 통해 코딩한다고 할 때 각 LED색깔 마다 구분하기 위한 고유한 번호가 필요할 것이다. 그러면 3bit가 있으면 7개의 LED를 각 숫자 하나하나에 할당할 수 있을 것이다. 이렇게 최소로 필요한 3bit와 같은게 엔트로피인 것이다. 그래서 수식화하면 다음과 같다.

$H(X) = - \sum_{i=1}^{n} p(x_i)log(p(x_i))$

단위는 bit로 나오게 된다.

Cross entropy

그런데 우리는 말하는 감자이기 때문에 모든 확률을 다 미리 알지 못한다. 대신 우리는 확률을 예상하는 것 정도는 할 수 있다. 그래서 그 진짜 확률을 $p(x_i)$, 예측한 확률을 $q(x_i)라고 하면 공식은 이렇게 된다.

$H(p, q) = - \sum_{i=1}^{n} p(x_i)log(q(x_i))$

KL-divergence(Kullback-Liebler divergence)

KL-divergence란 이 둘의 차이를 뜻하는 것이다. 그래서 공식은 다음과 같이 된다.

$D_{KL}(P||Q) = - \sum_{i=1}^{n} p(x_i)log(q(x_i)) + \sum_{i=1}^{n} p(x_i)log(p(x_i))$

= H(P,Q) - H(P)

= $\sum_{i=1}^{n} p(x_i)log(\frac{p(x_i)}{q(x_i)})$

KL-divergence는 두 가지 특성이 있다.

  1. KL(P,Q) $\geq$ 0 왜냐하면 cross entropy는 항상 entropy보다 크기 때문이다.
  2. KL(P,Q) $\neq$ (Q,P) KL-divergence는 거리개념이 아니라는 뜻이다. 왜냐하면 비대칭적이기 때문이다.

◼︎ Multi-class(multinomial) - classification: Softmax

이렇게 여러개를 classificate해야 할 때에 대한 이야기이다. 그러면 식이 다음과 같이 바뀌게 된다.

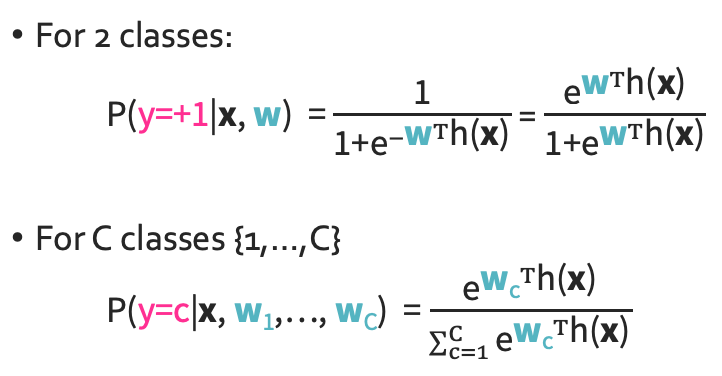
◼︎ False positives, false negatives, and confusion matrix

어쨋든 우리 맘대로 기준을 정해서 한거니까 우리가 좋다고 했는데 실제로 안좋고 안좋다 했는데 좋은경우도 있고 그럴 것이다. 그것을 표로 나타낸 것을 confusion matrix라고 한다.

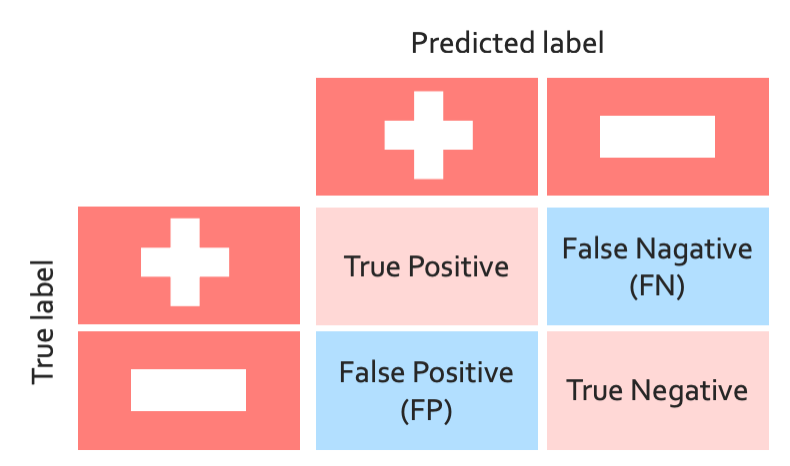
그래서 accuracy를 구하기 위해서는 true positive와 true negative만 분자에서 더하면 된다. Multi일때는 대각성분만 더하면 된다.

accuracy = $\frac{sum\,of\,true\,precentage}{100%}$

You may also enjoy

CA - chapter 5 Large and Fast: Exploiting Memory Hierarchy

9 minute read

이제 우리는 전체적인 CPU의 구조에 대해 이해할 수 있게 됐다. 그런데 우리가 자세히 다루지 않고 계속 사용하던 것이 있다. 바로 memory이다. gate나 mux등을 통해 많은 것을 만들 수 있지만 저장공간에 대한것은 아무 설명 없이 그냥 사용했다. 이번 장에는 이 memor...

Moment 2 - Review of 2024

2 minute read

열심히 블로그 쓴다고 한지 거의 4달만에 글을 다시 씁니다. 이거 굉장히 귀찮긴 하네요;;; 벌써 2025년이 돼서 개강도 했는데 이제야 24년 사진들을을 올려볼까 합니다. 24년은 제 인생에서 제일 행복한 해였던것 같습니다. 입시에서 벗어났다는 해방감도 있고 작년에 정말 많은...

ES - Week2

less than 1 minute read

https://nbviewer.jupyter.org/github/coolstone2000/coolstone2000.github.io/blob/2edbb9f3fc55fbfd2bba247b27114aaab578b5ad/files/2022142255%EC%A0%95%EC%84%9D%EC...