ML - Lecture 7: Regularized regression
◼︎ Geometric intuition for ridge regression
우선 2D일때의 ridge regression을 적용해 볼 것이다. 우선 2D일때 ridge regrssion의 식은 다음과 같다.
$RSS(w) + \lambda \left\|w\right\|^2_2= \sum_{i=1}^{N}(y_i - w_0h_0(x_i)-w_1h_1(x_i))^2 + \lambda (w_0^2+w_1^2)$
$RSS(w)$ part
일단 $\sum_{i=1}^{N}(y_i - w_0h_0(x_i)-w_1h_1(x_i))^2$ 이 부분만 뜯어서 보면 전개했을 때 우리가 흔히 ellipse(타원)꼴이라고 하는 $x^2+y^2+axy$꼴이 보이지 않나?
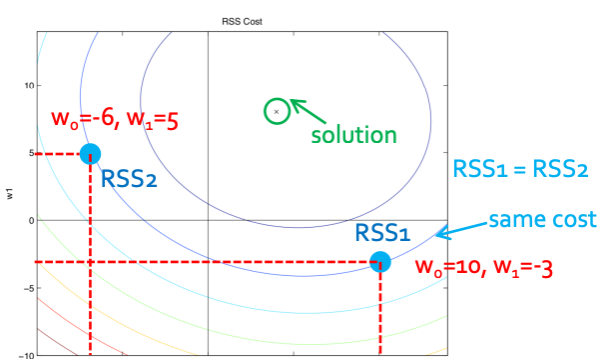
가운데의 점은 이 타원 식이 0이 되는 solution일 것이다. 그리고 나머지 선들은 $w_0, w_1$의 숫자에 따라 그려질 것이다. 그래서 RSS1과 RSS2는 값은 다르지만 선이 같은곳에 있으므로 same cost를 가진다는 것을 알 수 있다.
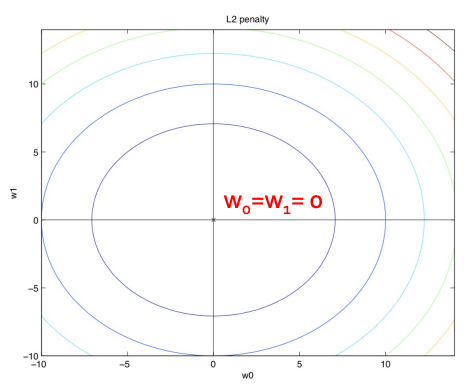
$\lambda \left|w\right|^2_2$ part
그리고 이제 $w_0^2+w_1^2$ 이 부분을 볼 것이다. 이 부분은 누가봐도 $x^2+y^2$인 원으로 보이지 않나? 그래서 그림은 원점을 중심으로 하는 원으로 그려지게 된다.
All together
그러면 이것을 합쳐서 생각해봐야할 것이다. 그걸 다룬 그림은 다음과 같다.
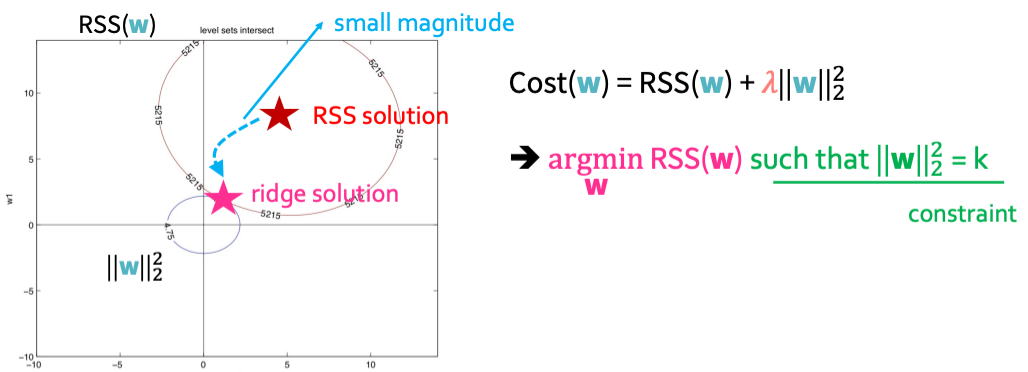
두 도형이 접하는 시기가 ridge solution이 될 것이고 이것은 라그랑주 승수법과 같다. $\lambda \left|w\right|^2_2$ 부분을 우리는 k라는 상수(constriant)로 볼 수 있을 것이다. 그런데 이 값은 $\lambda$에 의해 값이 결정 될 것이고 $\lambda$가 증가면 k는 감소하게 된다.
◼︎ Geometric intuition for LASSO regression
LASSO나 ridge나 RSS의 식은 정확히 같은 식을 가진다. 하지만 달라지는 부분은 뒷부분이다. 2D LASSO의 식은 다음과 같다.
$RSS(w) + \lambda \left\|w\right\|_1= \sum_{i=1}^{N}(y_i - w_0h_0(x_i)-w_1h_1(x_i))^2 + \lambda (|w_0|+|w_1|)$
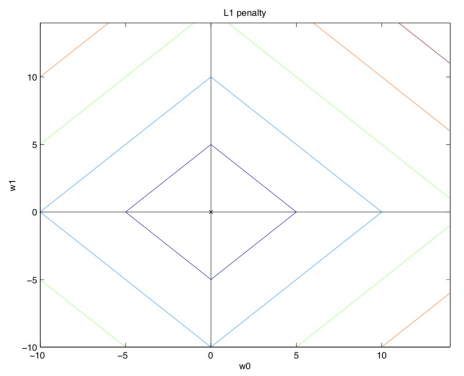
$\lambda \left|w\right|_1$ part
그래서 $|w_0|+|w_1|$ 이 부분만 보면 된다.
이 부분은 우리가 $|x|+|y|$ 절대값 함수로 알고 있는 이 마름모 꼴의 함수를 그리면 될 것이다.
All together
RSS와 합쳐서 생각한 그림은 다음과 같다.
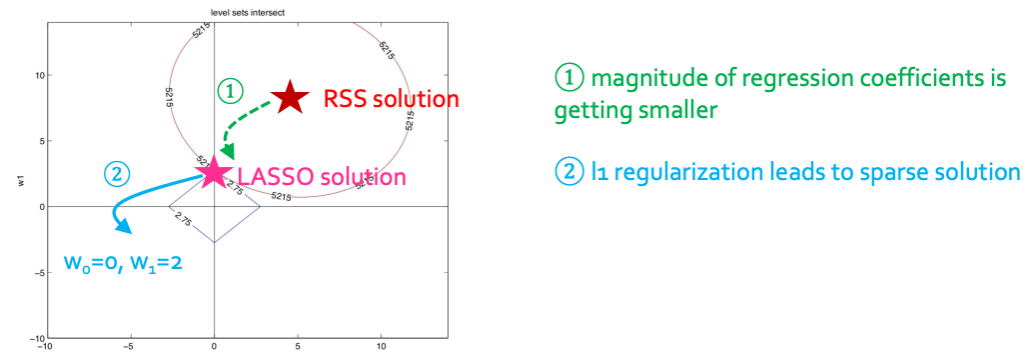
그림처럼 점점 coefficient가 작아지다가 LASSO solution부분에서 정확히 0이 되어 사라지게 될 것이다.
◼︎ How to choose $\lambda$
$\lambda$를 구하는 방법에 대해 조금 더 생각해 볼 것이다. 일단 data set을 어떻게 나누는지에 대해 다시 생각해 봐야 한다.
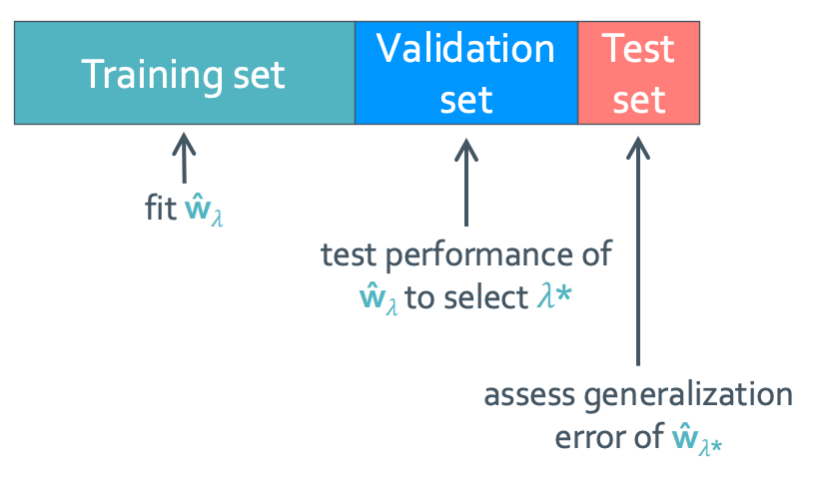
앞에서 다루었듯이 training set, validation set, test set 세 파트로 나눠야 한다. 그런데 항상 이렇게만 하면 문제가 생기게 된다. 이 고정된 validation set이 확실히 다양한 모델의 성능을 비교할 만큼 set이 충분할까? 답은 “그렇지 않다”이다. 그래서 좀 더 충분해 질 수 있도록 우리는 validation set을 여러개 만들 것이다.
K-fold cross validation
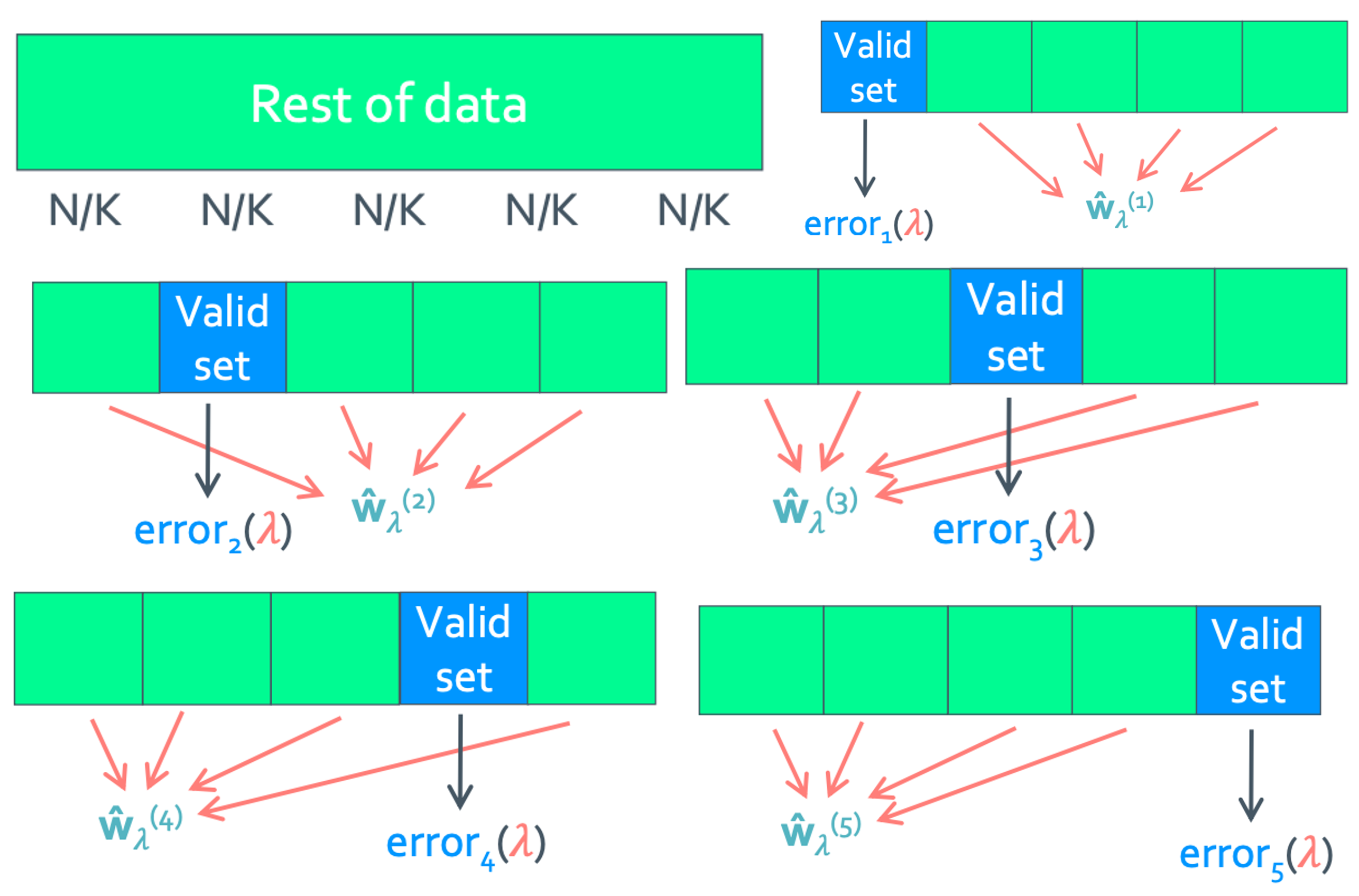
이렇게 모든 data를 K구역 만큼 나눈 뒤 각 구역의 validation set을 모두 사용하는 것이다.
- compute average error: $CV(\lambda) = \sum_{k=1}^{K}error_k(\lambda)/K$
이렇게 정의된 $CV(\lambda)$를 최소화 하는 $\lambda^*$를 구하면 되는 것이다.
그리고 보통 K의 숫자로 자주 쓰이는 것은 5 또는 10이 자주 쓰인다.
어 이게 아닌가?
