ML - Lecture 6: LASSO regression
저번 lecture에서는 ridge regression을 다루었으니 이번 lecture에서는 다른 regularization인 LASSO regression에 대해 다룰 것이다.
◼︎ Feature selection
w의 사이즈가 크면 클수록 모든 계산을 다 해줘야 하기 때문에 굉장히 계산량이 많아 expensive할 것이다. 그런데 만약 $\hat{w}$가 spares(0이 많다는 뜻)하면 0인거는 계산할 필요없고 0이 아닌 것만 계산 하면 돼서 계산량이 많이 줄게 된다. Ridge regression같은 경우에는 완벽하게 0을 만들지 못한다. 그런데 LASSO에서는 그게 가능해지면서 계산량을 많이 없앨 수 있게 된다. 그래서 0이 아닌 feature selection을 하는 것이다.

???: 누가 초코만 먹었냐
◼︎ Option 1: All subsets or greedy variants
모든 것을 다 고려하면 너무 많을 것이다. $2^{D+1}$개로 늘어나는데 어떻게 이걸 할 수 있을까?
Greedy algorithms
그걸 좀 해소할 수 있는 방법이다.
- Forward stepwise: simple한 것들을 하나하나 추가해 보는 것
- Backward stepwise: 필요 없는 것들을 줄여나가는 것
- Combining forward and abckward steps: 둘이 합친거
그럼에도 불구하고 굉장히 비효율적이다.
◼︎ Option 2: Regularization
그래서 ridge regession과 같은 regularization을 통해 해소를 한다. 그런데 앞에서 말했듯 ridge regession은 w를 완전히 0으로 만들지 못한다. 그래서 다음과 같은 아이디어를 고안했다.
- Feature selection
- 시작은 모든 feature를 고려한다.
- Coefficient가 0에 가까운 것은 그냥 0으로 퉁쳐버린다.
- 0이 아닌 coefficient만 select 될 것이다.
LASSO (Least Absolute Shrinkage and Selection Operator, L1-norm)
Total cost = measure of fit + measure of magnitude of coefficients
- If $\lambda = 0$: $RSS(w)$, $\hat{w} = \hat{w}_{Least Square}$
- If $\lambda = \infty$: $\hat{w} = 0$이다. 아니면 $\infty$가 될 것이다.
- If 0 $\lt \lambda \lt \infty$ : 0 $\leq$ $\left|\hat{w}\right|_1$ $\leq$
$\left| \hat{w}_{LS} \right|_1$
Coefficient path
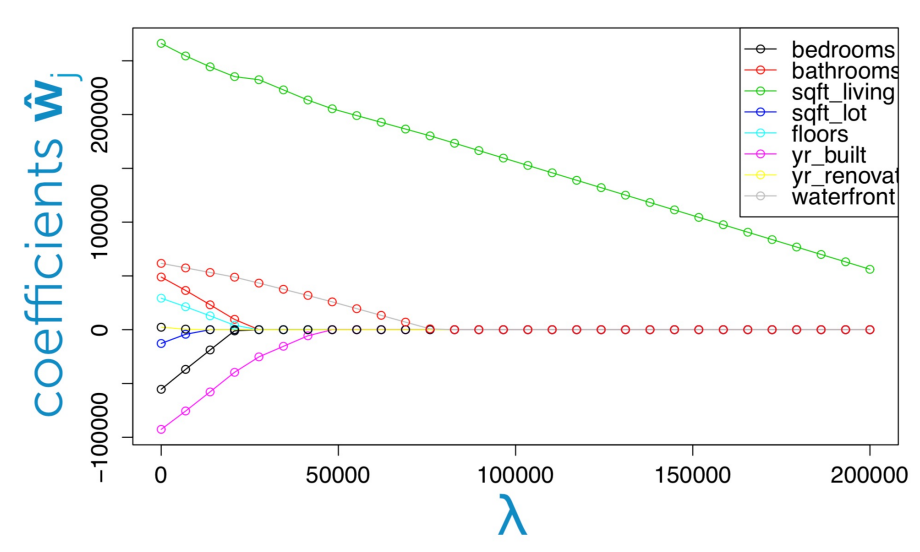
Ridge와 달리 0이 되는 것을 볼 수 있다.
◼︎ Fitting the lasso regression model(for given $\lambda$)
Optimizing the lasso objective
큰 문제가 있다. $\frac{\partial |w_j|}{\partial w_j}$ 이 미분 $w_j$일 때 어떻게 하지? 만약 계산했다고 치더라도 closed form이 없어서 불가능 하다.
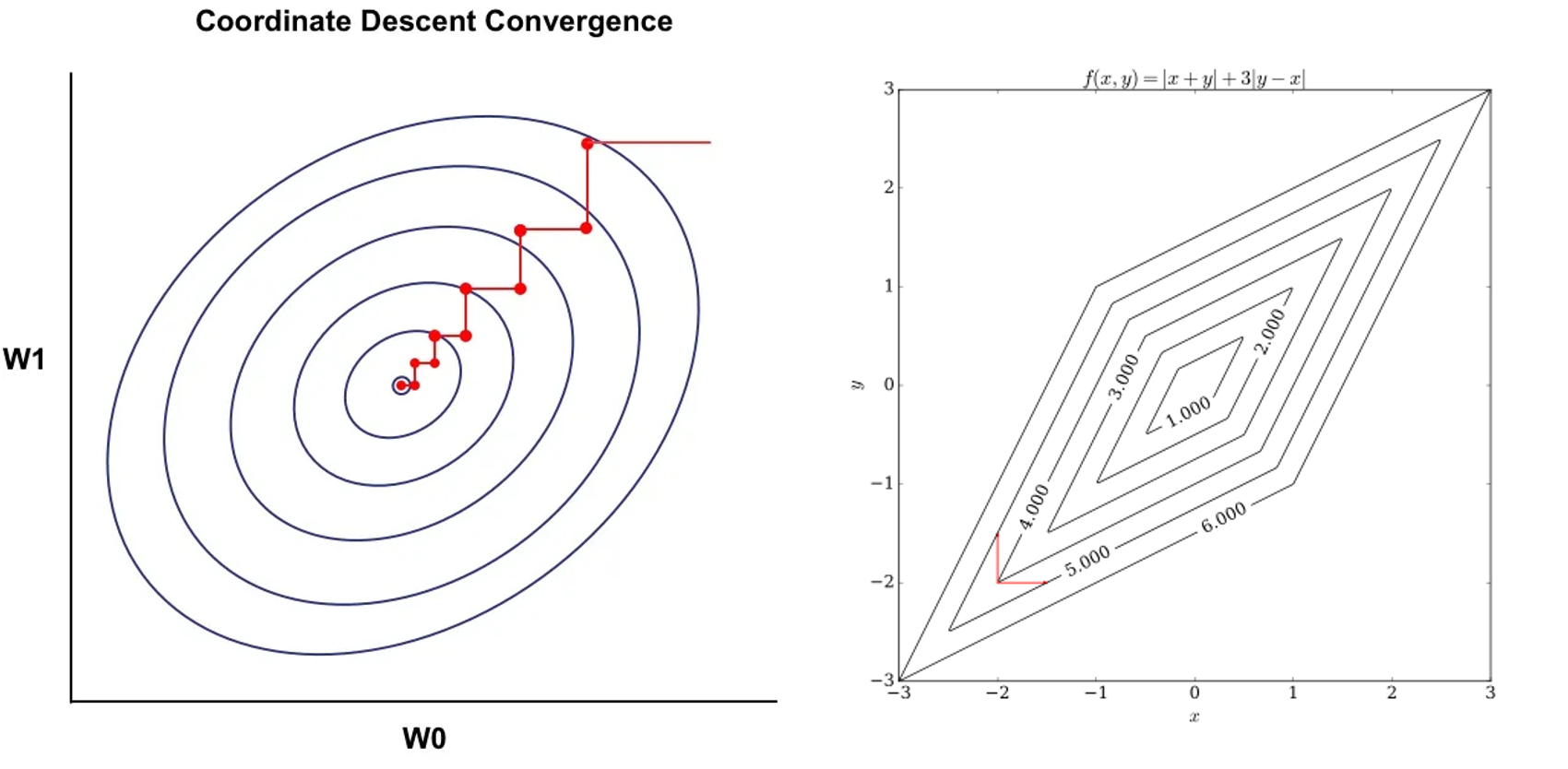
Aside 1: Coordinate descent
- 목적: minimzie some function g, 즉 한쪽 축에 대해서만 미분하는것
Gradient decent같은 경우는 모든 방향으로 다 갈 수 있지만 coordinate descent는 무조건 축 방향만으로 움직일 수 있다. 그러면 축을 정해야 하는 데 이것은 어떻게 정할까? 그냥 random하게 정하거나 RR방식으로 정하거나 여러 방법이 있다. 그런데 어떤 방식을 쓰든 step size를 골라야 할 필요가 없다. 그래서 유용하지만 병렬화(이전 값을 기억해야 함)가 힘들고 non smooth 일 때는 안 좋을 수 있다.
Aside 2: Normalizing features
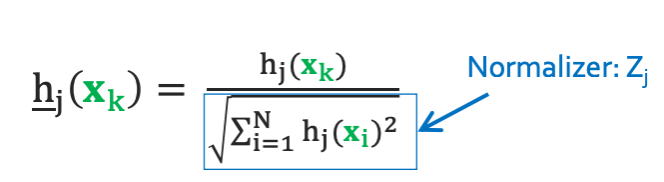
항상 normalizer를 계속 저장하고 있어야 한다. 이것의 장점은 feature들의 정도나 단위가 다를 텐데 nomarlization을 통해 모든 feature를 동일한 기준 안에서 비교할 수 있다. $\underline{h}$라는 것은 normalized 됐다는 뜻이다.
Aside 3: Coordinate descent for unregularized regression(for normalizezd features)
Normalize를 적용한 식은 다음과 같다.
$RSS(w) = \sum_{i=1}^{N}(y_i - \sum_{j=0}^{D}w_j\underline{h_j}(x_i))^2$
이것을 all coordinates $w_j$에 대해 모든 partial을 구할 것이다.
- $\rho$: $w_j$를 포함하지 않은 w값

◼︎ Coodinate descent for lasso(for normalized features)
우선적으로 $\hat{w_j}$를 가정해야 한다.
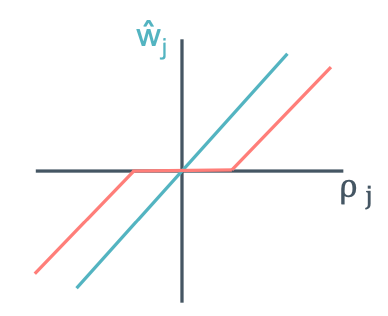
이 그림에서 보면 $[-\lambda / 2, \lambda / 2]$지점에서 0이 되는 것을 볼 수 있다. 이 지점들이 feature를 0으로 만드는 곳이다. 이제 이렇게 만들었는데 그러면 어느 지점에서 converge를 멈춰야 하는 것일까?
점점 갈수록 step이 작아질 것이다. 그러면 max step < $\epsilon$이 됐을 때 멈추면 되는 것이다.
◼︎ Deriving the lasso coordinate descent update(for unnormalized features)
$RSS(w) + \lambda \left\|w\right\|_1= \sum_{i=1}^{N}(y_i - \sum_{j=0}^{D}w_jh_j(x_i))^2 + \lambda \sum_{j=0}^{D}|w_j|$
이것은 최종적인 LASSO regression의 식이다.
Part 1: Partial of RSS term
Part 2: Partial of L1 penalty term
- Subgradients: any plane that lower bounds function
- L1’s subgradients:
$\lambda \partial|w_j|= \begin{cases} -\lambda & w_j < 0 \newline [-\lambda, \lambda] & w_j = 0 \newline \lambda & w_j> 0 \end{cases}$
$\partial w_j[\operatorname{lasso \, cost}]= \begin{cases} 2z_jw_j-2\rho_j - \lambda & w_j < 0 \newline [-2\rho_j-\lambda, -2\rho_j + \lambda] & w_j = 0 \newline 2z_jw_j-2\rho_j + \lambda & w_j> 0 \end{cases}$
그렇기 때문에 이 $\partial w_j[\operatorname{lasso \, cost}]$ = 0을 만족하게 하면 된다.
$\hat{w_j}= \begin{cases} (\rho_j+ \lambda / 2)/z_j & \rho_j < -\lambda / 2 \newline 0 & \rho_j \; in [-\lambda / 2, \lambda / 2] \newline (\rho_j-\lambda / 2)/z_j & \rho_j > \lambda / 2 \end{cases}$
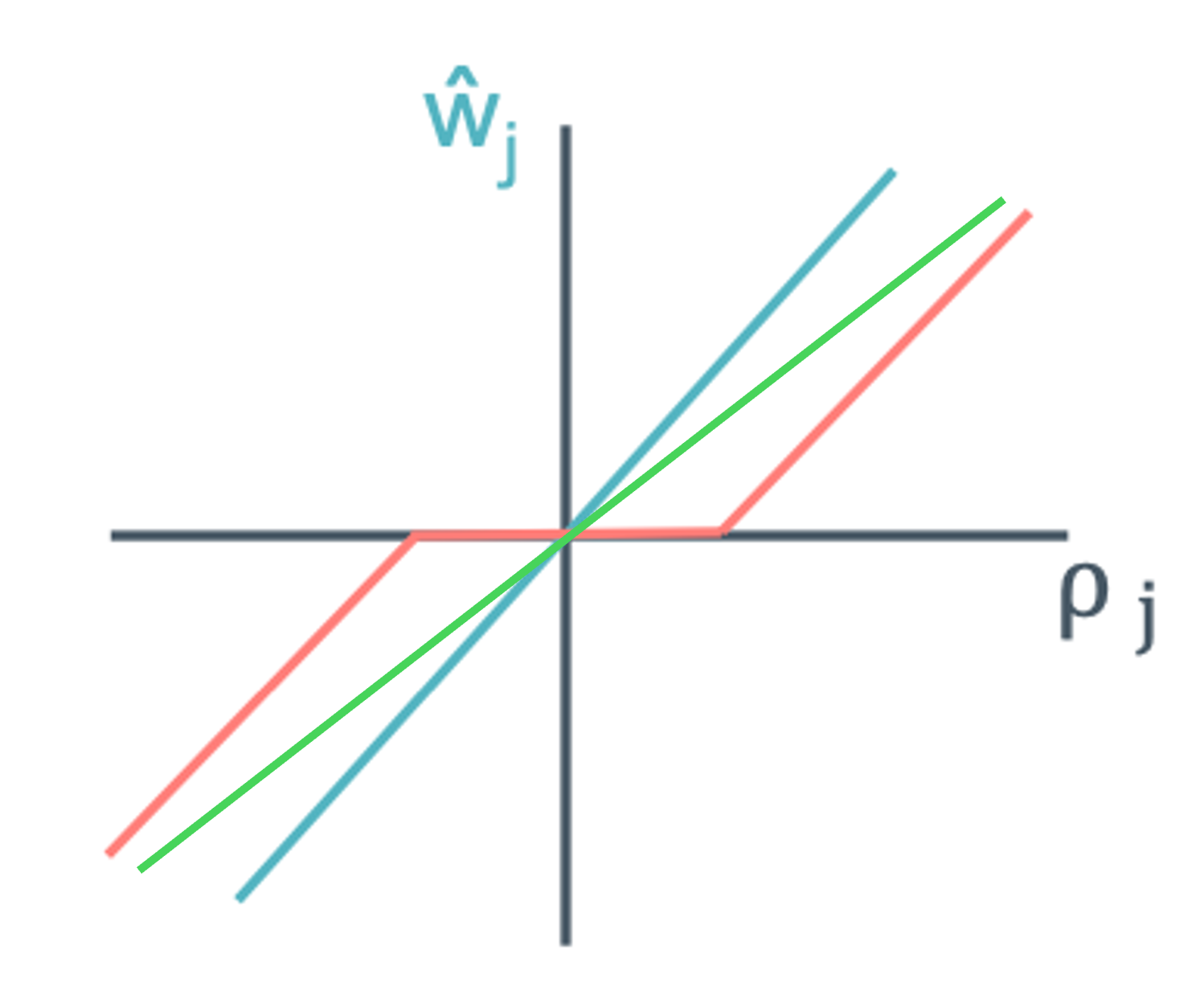
그래서 표는 이렇게 되는 것이고 초록색 선은 ridge regression이라고 생각하면 된다.
◼︎ 최종적으로…
과연 이게 제일 좋은 방법이 맞을까? 생각보다 LASSO도 계산이 쉽지 않고 그래서 다른 응용버전이 존재하기도 한다. 그리고 항상 ridge보다 좋다고도 못하고 일단 완벽한 최고의 방법은 없는 것이다. 그래서 두개 합쳐서 쓰기도 하고 여러가지 방법들로 열심히 성능을 올리기 위해 노력하고는 있다.