ML - Lecture 5: Ridge regression
앞의 lecture에서 complexity가 많아지면 overfitting될 수 있다고 하였다. 특히 overfitting에 영향을 크게 주는 parameter는 $\hat{w}$이다. $\hat{w}$가 너무 크면 필연적으로 overfitting해져버린다. 이러한 overfit된 model을 좀더 general하게 만들려면 어떻게 해야하는가에 대해 다룰것이다. 이것을 regularizaion(정규화) 라고 한다.
◼︎ Overfitting of linear regression model more generically
우선 두 가지 요소가 overfitting의 가능성을 높이게 된다.
- Lots of inputs
- lots of features
$ y_i = \sum_{j=0}^{D}w_jh_j(x_i) + \epsilon_i$
w와 h가 많으면 overfit 해버린다. (D가 크다는 뜻)
Data의 개수가 overfitting에 주는 영향력
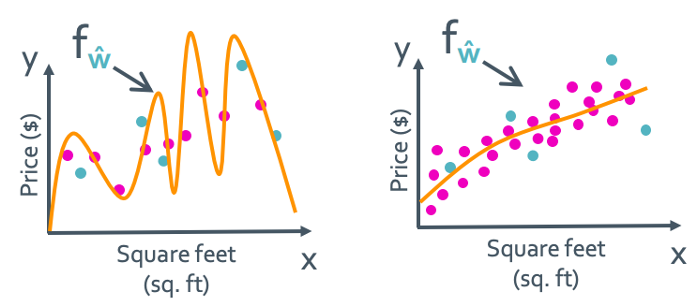
위의 그림 처럼 training data가 많아지면 overfitting의 가능성이 줄어든다. 대신 cost는 증가한다.
input의 개수가 overfitting에 주는 영향력
우선 overfitting하지 않기 위해서는 representative한 data set을 input으로 잘 설정해야한다. 그런데 이것이 정말 쉽지 않은 과정이다. Input이 한 개일때도 힘들지만 input이 d개가 됐을때는 얼마나 더 힘들어질까?
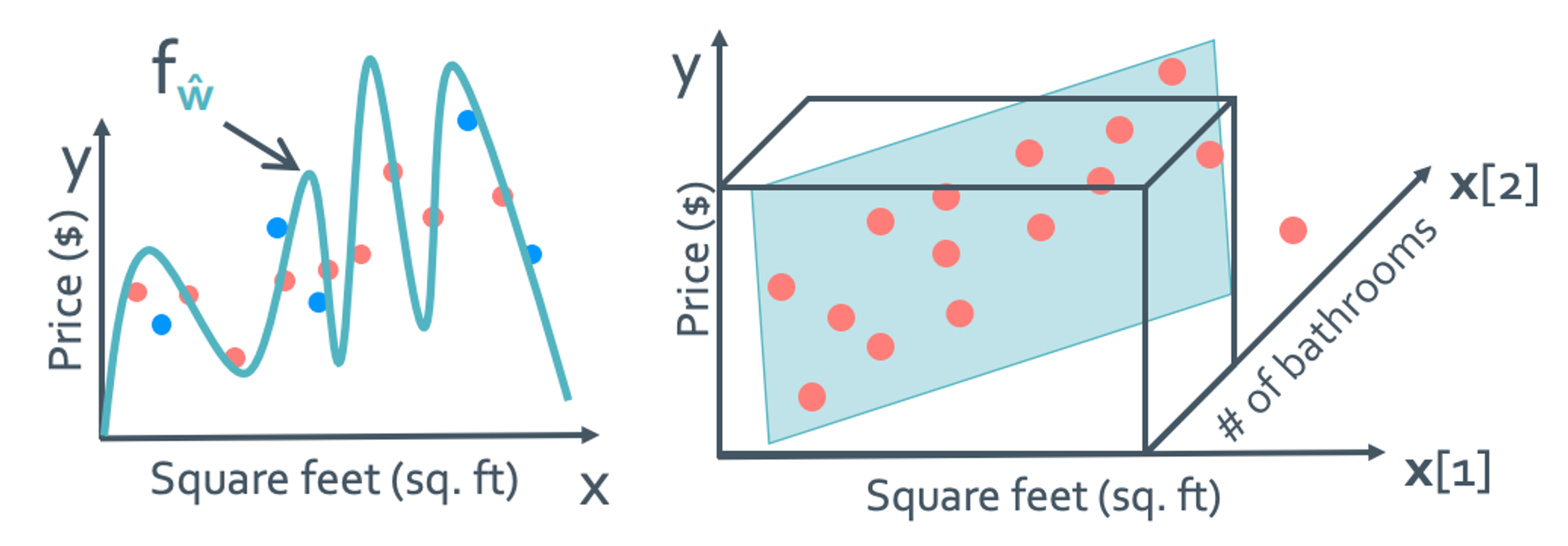
위의 방식으로는 overfit을 피하기가 굉장히 힘들어진다. 그래서 남은 요소인 w를 건들일 것이다.
◼︎ Adding term to cost-of-fit to prefer small coefficients
우리는 지금까지 model의 신뢰도를 말하는 cost를 $min(y-\hat y)$로 사용했다. 하지만 이것으로는 overfitting의 문제가 일어나게 돼어 cost의 정의를 좀 수정할 필요가 있다. 우리가 cost가 보증해줬으면 좋겠는 것은 다음과 같다.
- How well function fits data (이건 이미 있던거고)
- Magnitude of coefficients (새로 추가한것)
Total cost = measure of fit + measure of magnitude of coefficients
어쨋든 total cost가 작아야 좋은 model이라고 하는것은 변치 않는다. 그래서 measure of fit와 measure of magnitude of coefficients을 balance있게 조절을 해야한다.
measure of fit가 작다는 것은 training data와 잘 맞는다를 뜻할 것이고
measure of magnitude of coefficients가 작다는 것은 not overfit이라는 뜻이다.
Measure of fit
이건 앞에서도 여러번 한것이다. 사실 여기에 딱히 변화를 주지는 않는다.
$RSS(w) = \sum_{i=1}^{N}(y_{i}-h(x_i)^T w)^2$
Measure of magnitude of coefficients
크기를 재는 법에는 여러가지가 있다. 그 중 3개만 일단 봐볼 것이다.
-
Sum: $\sum_{j=0}^{D} w_j$
-
Sum of absolute value: $\sum_{j=0}^{D} |w_{j}|$ (L1 norm → LASSO)
-
Sum of sqaures: $\sum_{j=0}^{D} w_j^2$ (L2 norm → Ridge regression)
이번 lecture에서는 L2 norm을 사용하여 ridge regression에 대해 다룰 것이다.
Total cost using L2 norm
Total cost = measure of fit + measure of magnitude of coefficients
이것이 최종적인 total cost function이다. 우리가 total cost를 최소로 하는 $\hat{w}$를 결정한다고 하자.
- If $\lambda = 0$: $RSS(w)$, $\hat{w} = \hat{w}_{Least Square}$
- If $\lambda = \infty$: $\hat{w} = 0$이다. 아니면 $\infty$가 될 것이다.
- If $0 \lt \lambda \lt \infty$ : $0\leq \left|\hat{w}\right| _{2}^{2} \leq $
$\left| \hat{w}_{LS} \right| _{2}^{2} $
$\lambda $ : tuning parameter = 이게 둘의 balance를 결정한다.
Bias-variance tradeoff
-
Large $\lambda$: High bias, low variance (w↓ → complexity↓)
-
Small $\lambda$: Low bias, high variance (w↑ → complexity↑)
Coefficient path
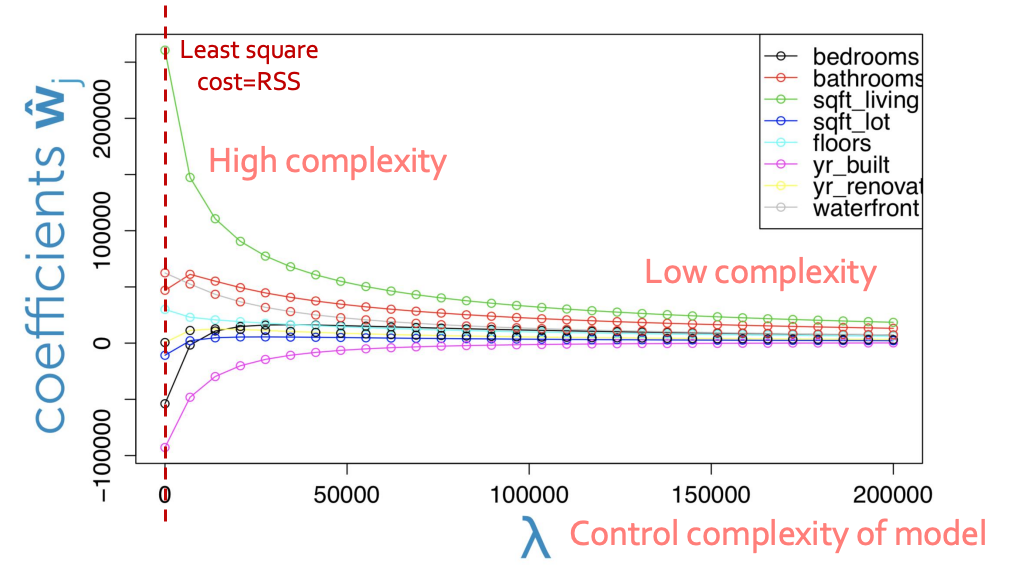
이 표를 보면 $\lambda$가 커지면 과하게 training 되는 것을 막아주고 있다.
◼︎ Fitting the ridge regression model($\lambda$가 주어졌을 때)
Step 1: Rewrite total cost in matrix
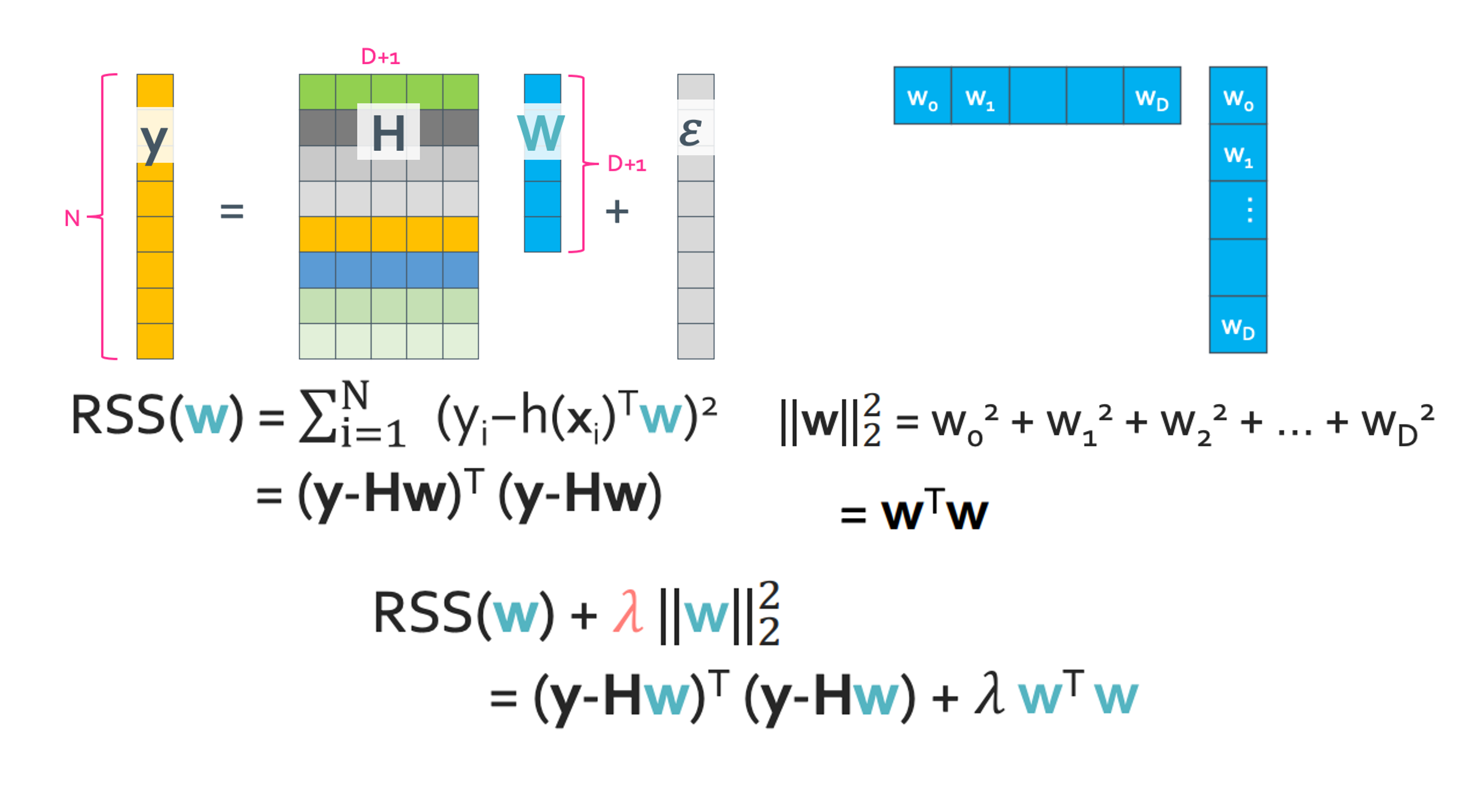
Cost function을 행렬로 나타내면 위 그림과 같다.
Step 2: Compute the gradient
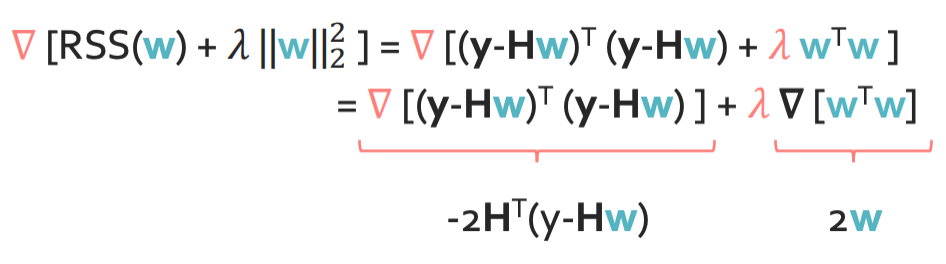
Step 3 approach 1: Set the gradient = 0
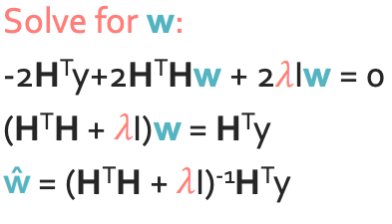
재밌는 사실은 $\lambda > 0$이면 항상 invertible하다. 왜냐하면 $\lambda$ 때문에 항상 행렬이 양정치가 되기 때문이다.
Step 3 approach 2: Gradient decent

partial은 예전의 cost와 똑같이 가고 앞에 $-2\eta \lambda$가 붙는다. 조심해야하는 것은 여기서 이미 $\lambda$는 아는 값이기 때문에 $\eta$를 찾는 것이다.
◼︎ Connect with MAP
우리가 베이즈 정리를 배울 때 이런식 꼴을 배웠다.
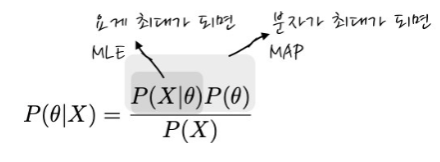
여기서 알 수 있듯 MAP이란 전체 사건을 통해 모수를 구하는 것이라고 생각하면 된다. 다음은 MLE와 MAP의 장단점이다.
| MLE | MAP | |
|---|---|---|
| Advantage | 사전정보가 필요 없음, 계산이 간편 | 과적합을 피할 수 있음, 데이터가 적어도 추정이 가능 |
| Disadvantaage | 과적합 가능성, 데이터가 적으면 학습이 잘 안될수 있음 | 사전 정보에 따라 결과 변경, 계산량이 많음 |
그런데 대체 왜 MAP을 뜬금없이 들고온걸까? 여기서 보여주려는 것은 MAP을 적용하면 신기하게 결과값으로 ridge regression을 한 것과 같은 값이 나오기 때문이다.
여기서의 가정은 gaussian 분포의 가정을 $w_i \sim \mathcal{N}(0, \tau^2)$
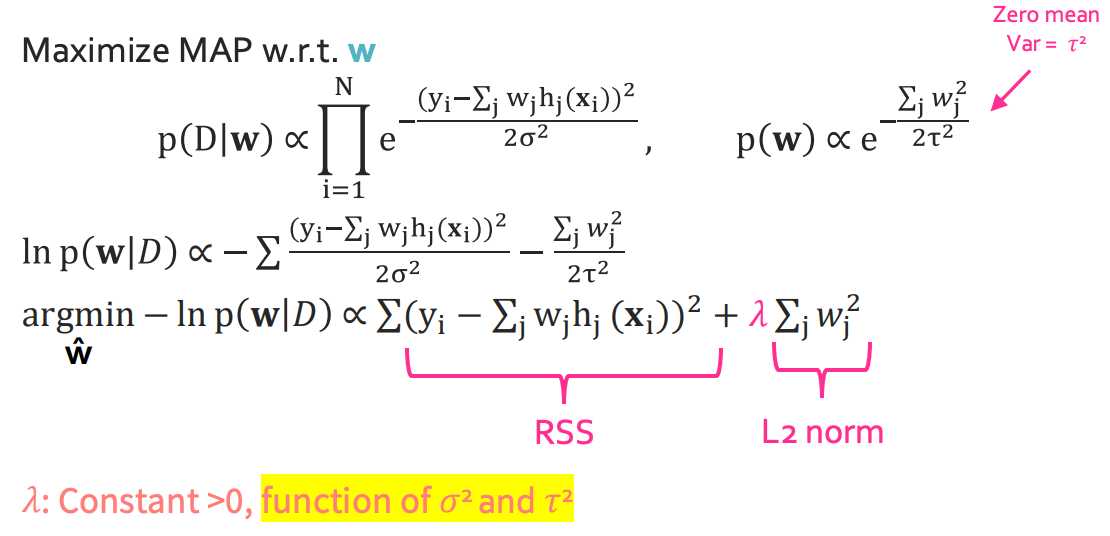
진짜 결과가 똑같이 나온다. 신기하다!
◼︎ How to choose $\lambda$
Hypothical implementation

우리가 여태까지 해온 방식은 이것이다. Training set에서 $\hat{w}_{\lambda}$를 구하고 test set을 통해 제일 작은 $\lambda$를 찾으면 된다. 그런데 이건 너무 opitimisic하다. 그래서 좀 추가를 해 볼것이다.
Practical implementation
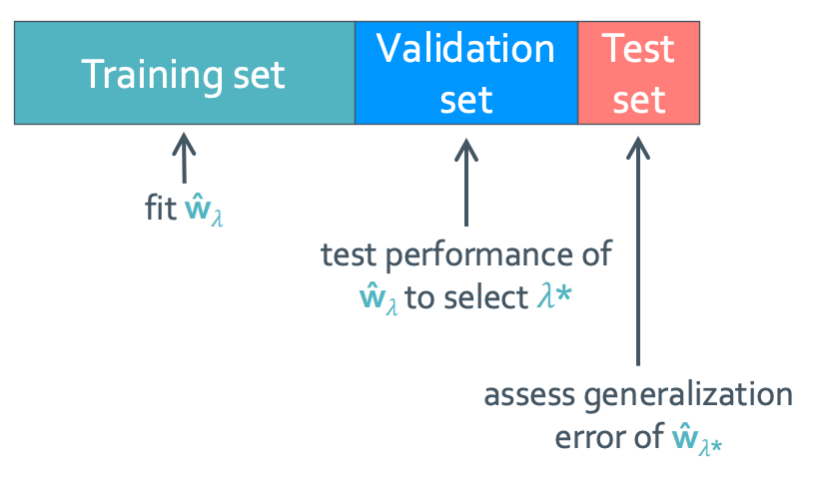
이건 위와 다르게 validation set을 추가했다. Training set에서 $\hat{w}_{\lambda}$를 구하고 validation set을 통해 제일 작은 $\lambda^*$를 찾는다. 그리고 test set에 딱 한번만 넣어본다. 여기서 성능이 안좋다고 나와도 수정을 하면 안된다.
수정 과정은 무조건 validation set을 통해 하는 것이다.
그리고 보통 이 비율을 80:10:10 혹은 50:25:25의 비율로 나눈다.
◼︎ How to handle the intercept
이것은 절편 즉 $w_0$를 어떻게 처리할지에 대한 이야기이다. 이것은 항상 상수 값으로 나오게 되는데 과연 이것도 낮은 수로 두는게 좋을까? 수식에 의하면 그래 보이긴 한다. 근데 overfitting과는 사실 별로 상관 없는 값이다. 그래서 다음 두 방법을 이용한다.
- Option1: Don’t penalize, 그냥 두기
- Option2: Center data first, 처음부터 data들을 0 근처에 있는 값들을 이용하여 small intercept가 나올 수 있게 training set을 이루게 하는 것이다. 이러면 진짜 무시해도 될 정도가 된다.