5 minute read

◼︎ Assessing performance

우리는 model과 algorithm을 통해 fitted function을 찾아낸다. 이렇게 function을 찾아내는 것을 prediction을 통해 하는데 만약 perfect predition이라면 perfection과 비교했을 시에 loss는 0이겠지만 실제로 내가 찾은 perfection은 그렇지 않다.

Measuring loss

  • Loss function: $L(y, f_{\hat{w}}(x))$
  • Actual value: $y$
  • Predicted value: $\hat{y} = f_{\hat{w}}(x)$

그래서 이 loss function을 어케 두느냐인데 전 lecture에서 언급한 그것이 나온다.

  • Absolute error: $L(y, f_{\hat{w}}(x)) = |y - f_{\hat{w}}(x)|$ (L1-norm)
  • Squared error: $L(y, f_{\hat{w}}(x)) = (y - f_{\hat{w}}(x))^2$ (L2-norm)

그런데 뭔가 parameter를 계속 많이 넣어주면 정보가 많으니까 더 정확해지고 좋은 모델이 나올것 같지 않을까? 이건 완전히 잘못된 생각이다. 몇 개 추가할때는 꽤나 regresssion이 정확해지는 것 처럼 보일 것이다. 그런데 다음 그림과 같은 상황이면 어떨까?


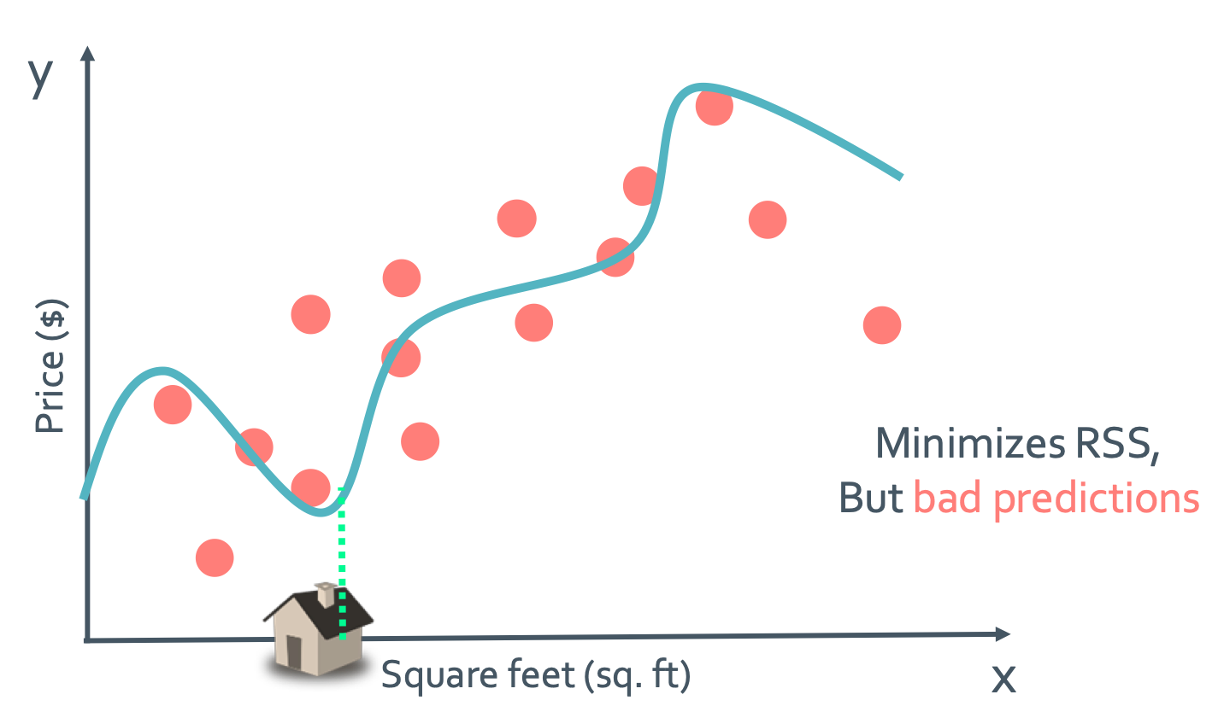
걍 눈으로만 봐도 경향성을 전혀 안따르고 있다는 것이 보이지 않은가? 그래서 마구잡이로 늘리기만 해서는 안되는 것이다.

◼︎ Assessing the loss

Part 1: Training error


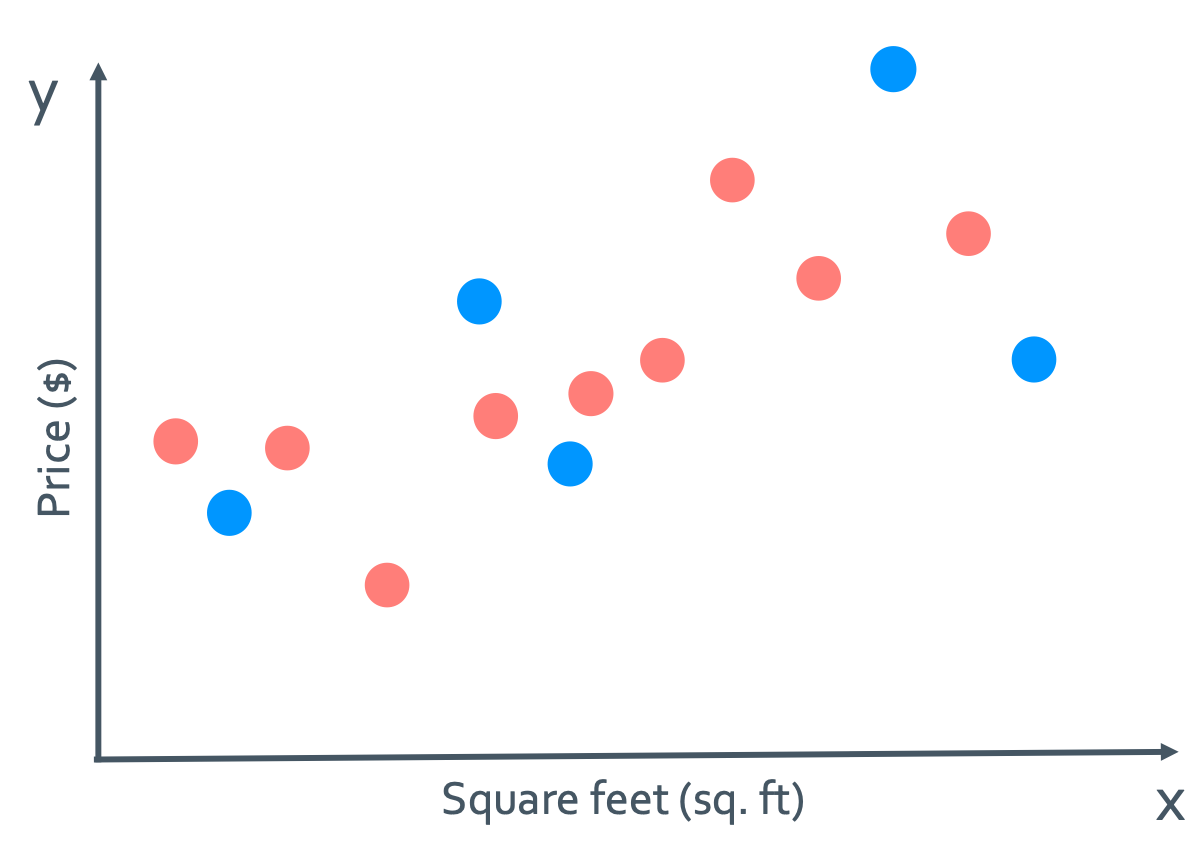
이것은 defining training data라고 하는데 학습을 시킬 때 모든 data를 다 넣는 것이 아닌 선택적으로 넣는 것이다. 그래서 이 그림에서는 파란색 data를 학습에 포함시키지 않는다.

• Compute training error

  1. Define a loss function $L(y, f_{\hat{w}}(x))$ (어떤 종류로 할지)
  2. Training error = avg.loss in training set = $\frac{1}{N_{training}} \sum_{i=1}^{N_{training}}L(y, f_{\hat{w}}(x))$

• Training error vs model complexity


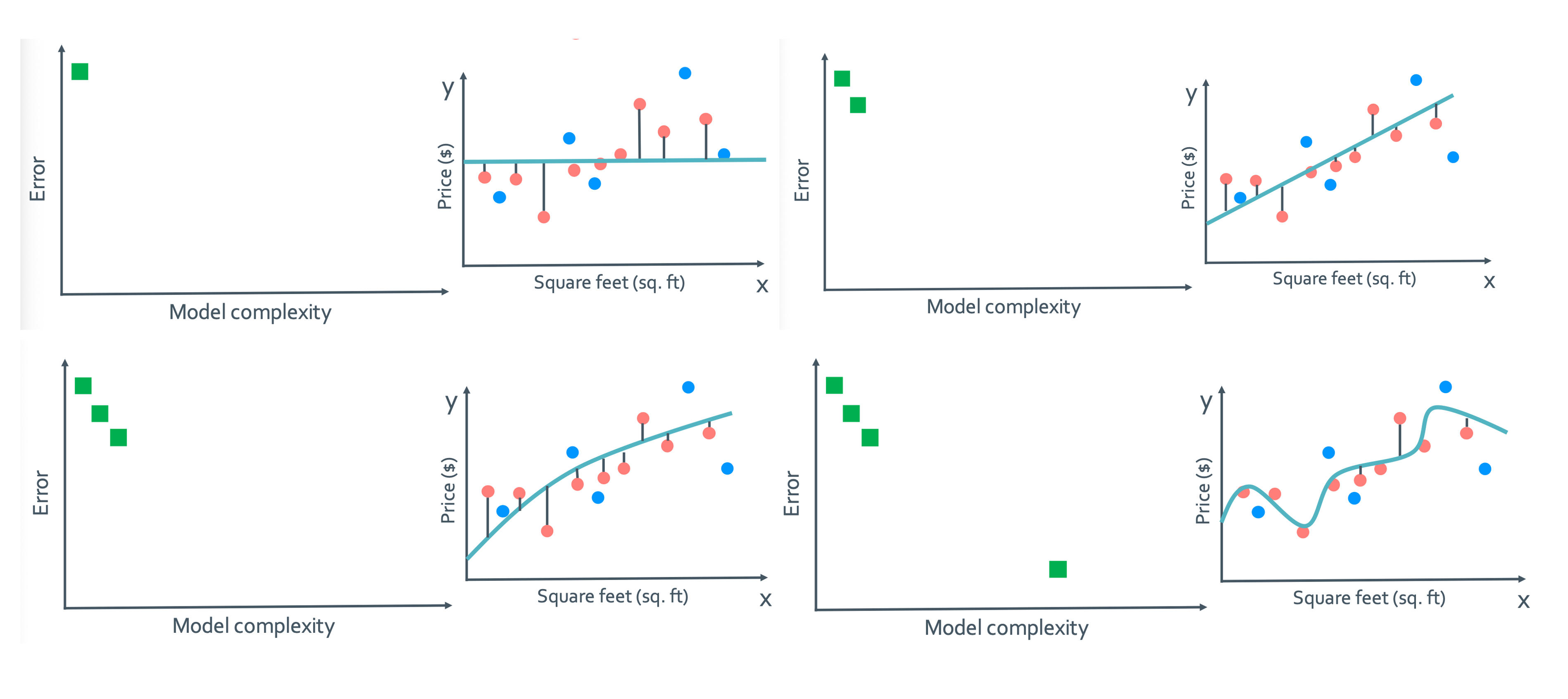
이걸 보면 알 수 있듯 model complexity가 높아질 수록 error는 감소한다. 그런데 과연 이렇게 training data를 뽑아서 만든 모델의 error가 작은게 good prediction이라고 할 수 있을까?

답은 절대 아니다이다. Training data가 전수조사를 한 것 아니면 좋지 않다. 근데 일단은 전수조사 자체가 불가능하다.

Part 2: Generalization (true) error

우리가 원하는 것은 모든 가능한 loss를 estimate하는 것이다. 즉, dataset에 없는 것을 잘 추정해야하는 것이다. 그래서 generalization error는 모델이 학습 데이터는 잘 동작하지만 새로운 데이터(dataset에 없던 것)에 대해 제대로 일반화 하지 못하는 경우인 것이다.

• Generalization (true) error definition

Generalization (true) error = $E_{x,y}[L(y,f_{\hat{w}}(x))] = \int L(y,f_{\hat{w}}(x))p(x,y) \, dxdy$

  • $E_{x,y}$: Average over all possible (x, y) pairs
  • $p(x, y)$: computationally not possible

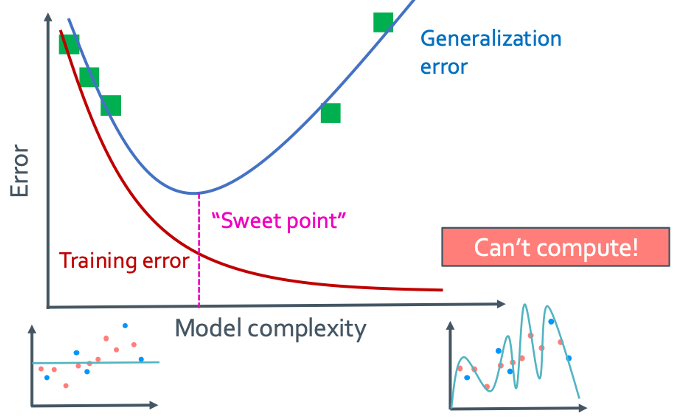
• Generalization (true) error vs model complexity


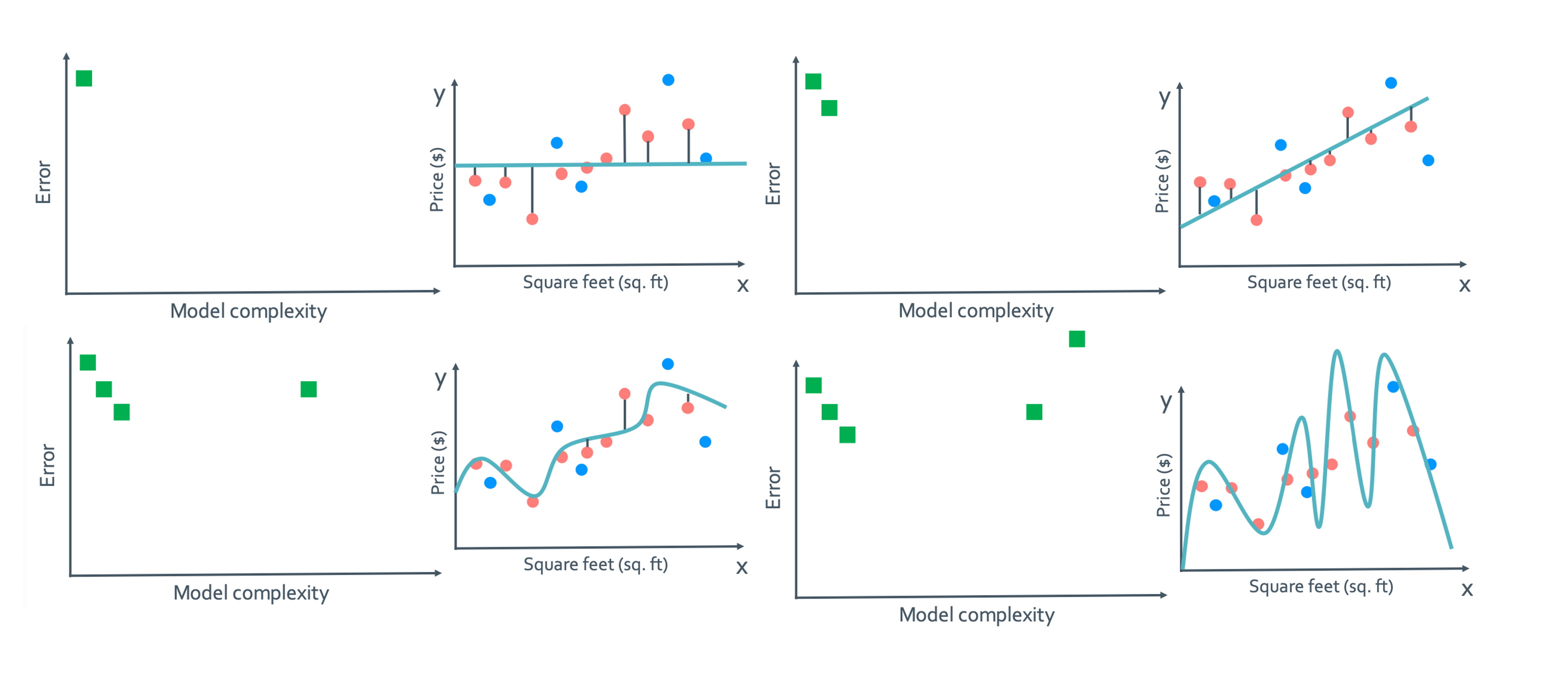
Generalization error는 모델이 복잡해질수록 낮아지다가 또 너무 많이 복잡해져버리게 되면 다시 error가 높아진다.

• Training vs Generalizaion

그래서 다음 그래프들은 training error와 generalization error를 비교한 그림이다.


Part 3: Test error

True error는 모든 dataset에 대하여 분석을 했다. 그런데 이걸 실제로 하는건 불가능에 가깝고 계산 양이 너무 많지 않을까? 그래서 고안된것이 test set이다. 우리가 가지고 있는 dataset을 training set과 test set로 나누는 것이다. 즉, data set = training set + test set. 이렇게 따로 testset을 빼는 것에는 이 것들이 전체를 대변할 수 있을 것이라는 가정이 있다. 그래서 true error 의 approximation은 test error가 된다.

• Compute test error

  • Test error = avg.loss in test set = $\frac{1}{N_{test}} \sum_{i\;in \; testset}L(y, f_{\hat{w}}(x))$


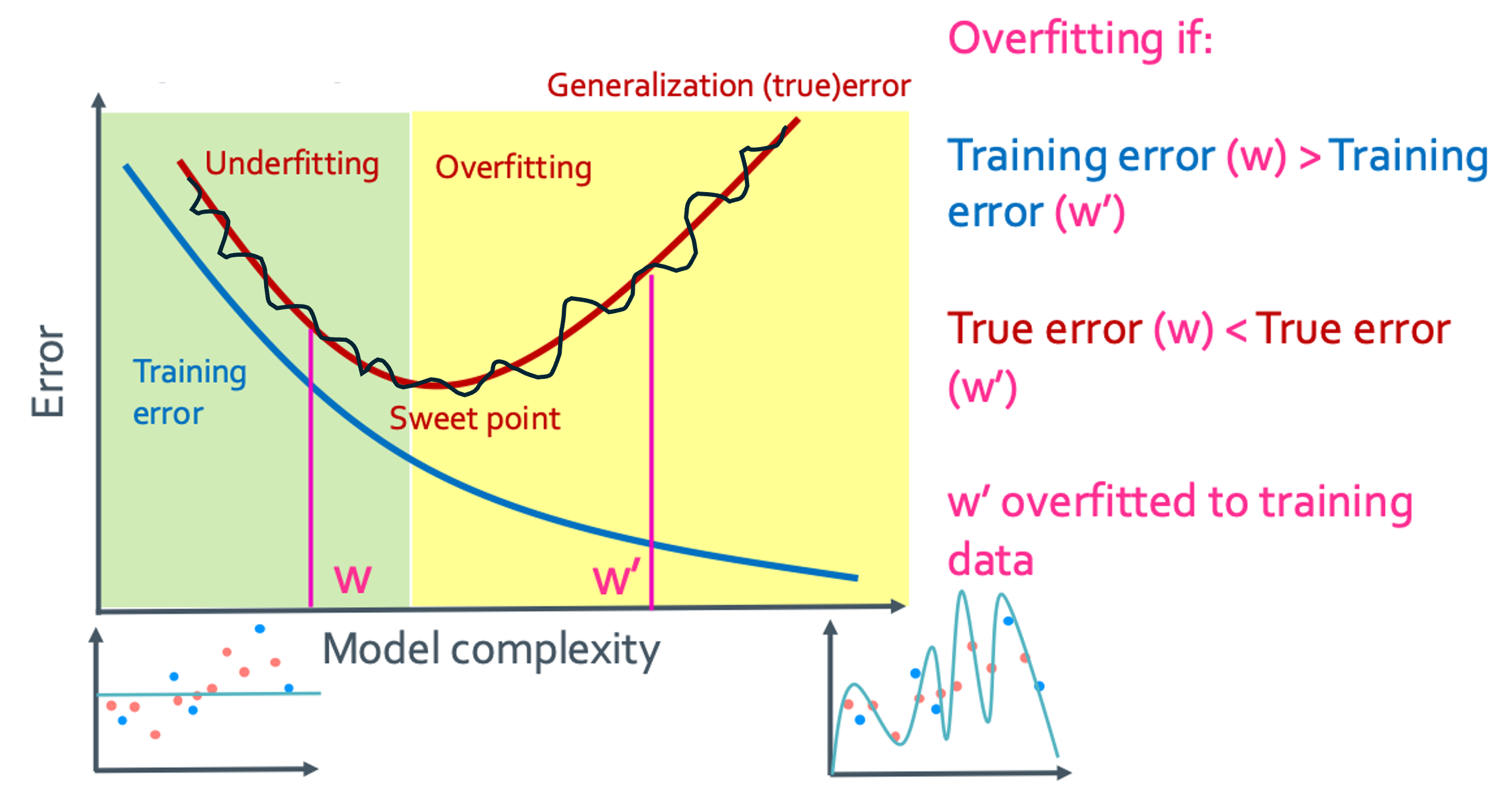
위의 그래프에서 검은색 그래프는 true error에 근접하고 있는 test error를 보여준 것이다. True error에 비해 test error는 noise가 껴있다.이 그래프들로 얼마나 fit한지를 알 수 있다.

  • Underfitting (과소적합): training set이 제대로 학습되지 않아 모델의 성능이 떨어지는 경우
    • Training error(w) > Training error(w’)
    • True error(w) > True error(w’)
    • 위 두개를 만족하면 underfitted

  • Overfitting (과대적합): 학습 모델이 지나치게 training data에만 초점이 맞춰져 일반화 성능이 떨어지는 경우
    • Training error(w) < Training error(w’)
    • True error(w) < True error(w’)
    • 위 두개를 만족하면 overfitted


???: even하게 익지 않았어요

Error vs amount of data


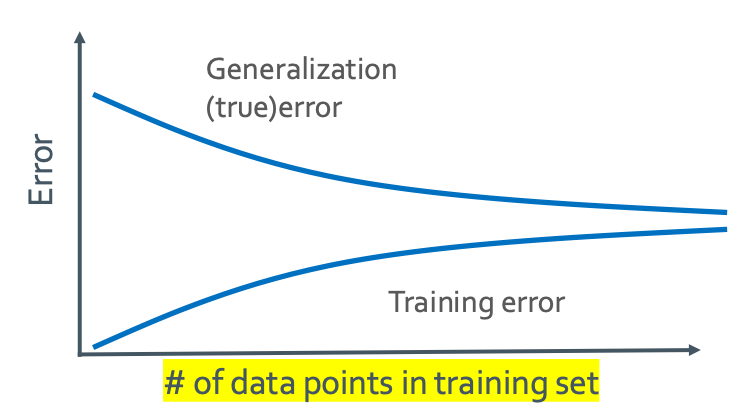
위의 그래프는 true error와 training error의 numbers of data 관계를 나타낸 것이다. x축이 model complexity가 아니니 주의하자.


◼︎ Training/test split

앞에서 data set = training set + test set 라고 했다. 그러면 training set 과 test set으로 나눠야 하는데 어떤 비율로 나눠야 하는지가 문제이다.


위의 경우에는 training set » test set일 때인데 이러면 $\hat{w}$가 너무 poorly estimated되어버린다. 아래의 경우는 test errror가 generalization (true) error를 제대로 대변하지 못한다.
($test error \ne appoximation\,of\, generalization$)

그래서 진짜 “even”하게 split을 잘 하는게 중요하다.

◼︎ 3 sources if error + the bias-variance tradeoff

  1. Noise(Irreducible, 줄일 수 없음)
  2. Bias(Reducible, 줄일 수 있음)
  3. Variance(Reducible, 줄일 수 있음)

우선 true function인 $f_{w(true)}$ 라는게 있다고 가정하자. 그것은 빨간색 그래프로 나타낼 것이다.

Noise


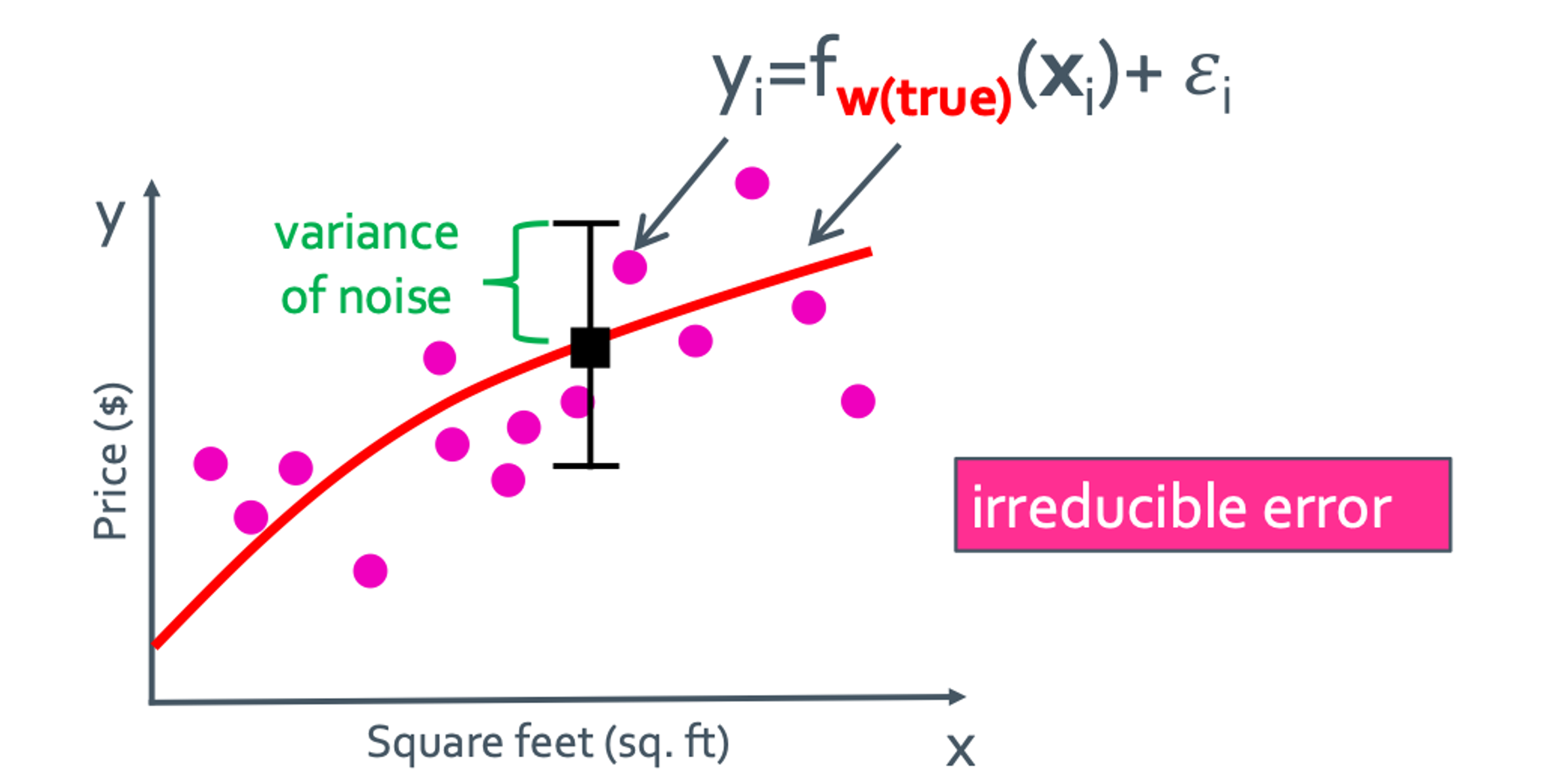
noise같은 경우는 $\epsilon_{i}$가 되는데 이것은 우리가 줄일 수가 없는 상수 값이다. 언제나 항상 일정하게 존재하게 된다.

Bias


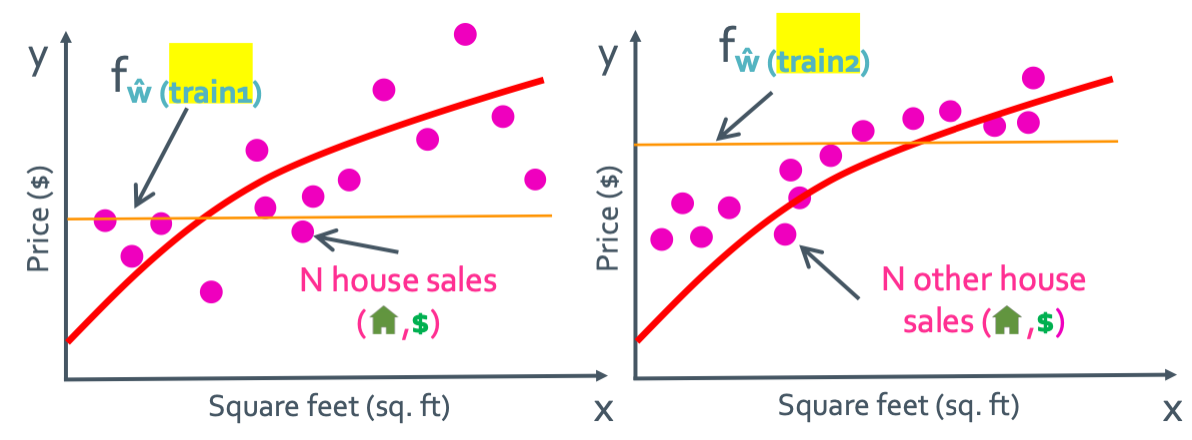
Bias가 매우 클때를 생각할 것이다. 그러면 매우 단순하게 생긴 constant function이라고 생각할 것이다. 그러면 위와 같이 서로 다른 training set들에 의해 $f_{\hat{w}}$가 여러개 나올 것이다. 그 중 제일 expectaion한 것을 $f_{\bar{w}}$로 둘 것이다.

$Bias(x) = f_{\bar{w}} - f_{w(true)}$

이것이 그렇게 해서 얻어낸 Bias(x)의 정의이다.


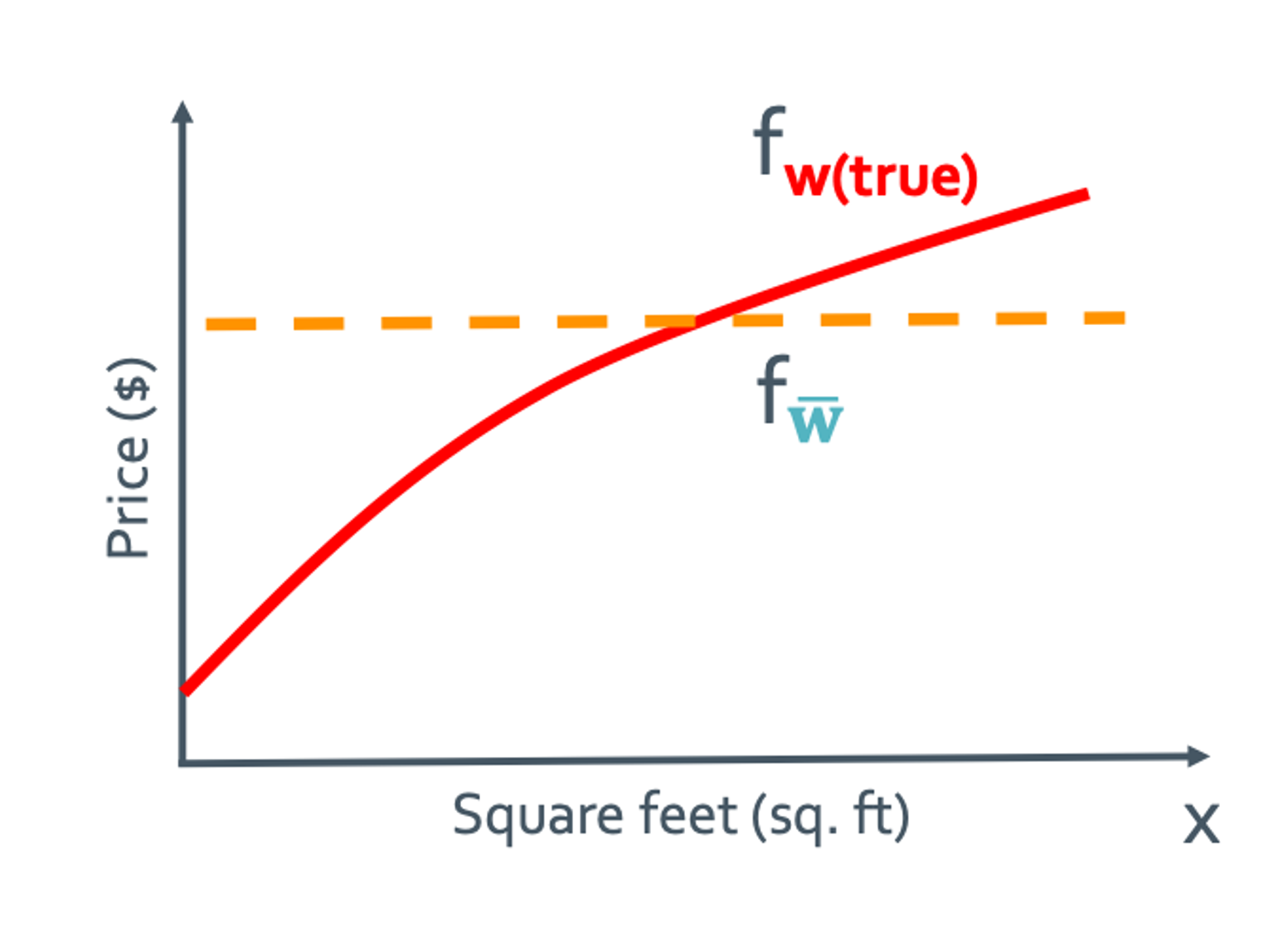
여기서 보면 알수 있는 것이 complexity가 낮으면 bias가 높고 variance가 낮다는 것이다.

Variance


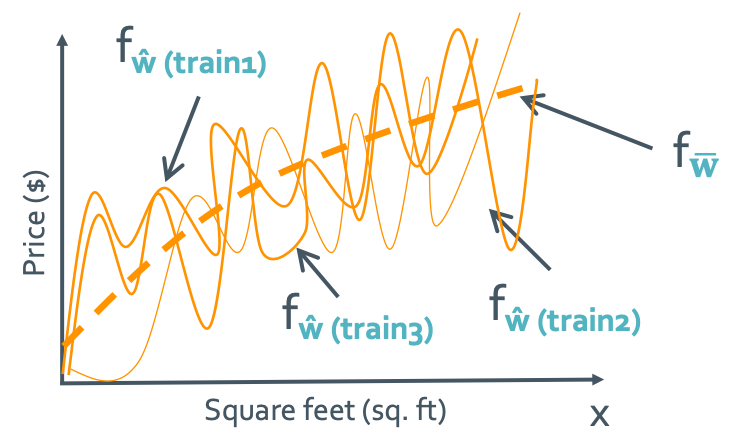
이번엔 variance가 매우 클때를 확인할 것이다. 그래서 high-order polynomial로 생각할 것이다.


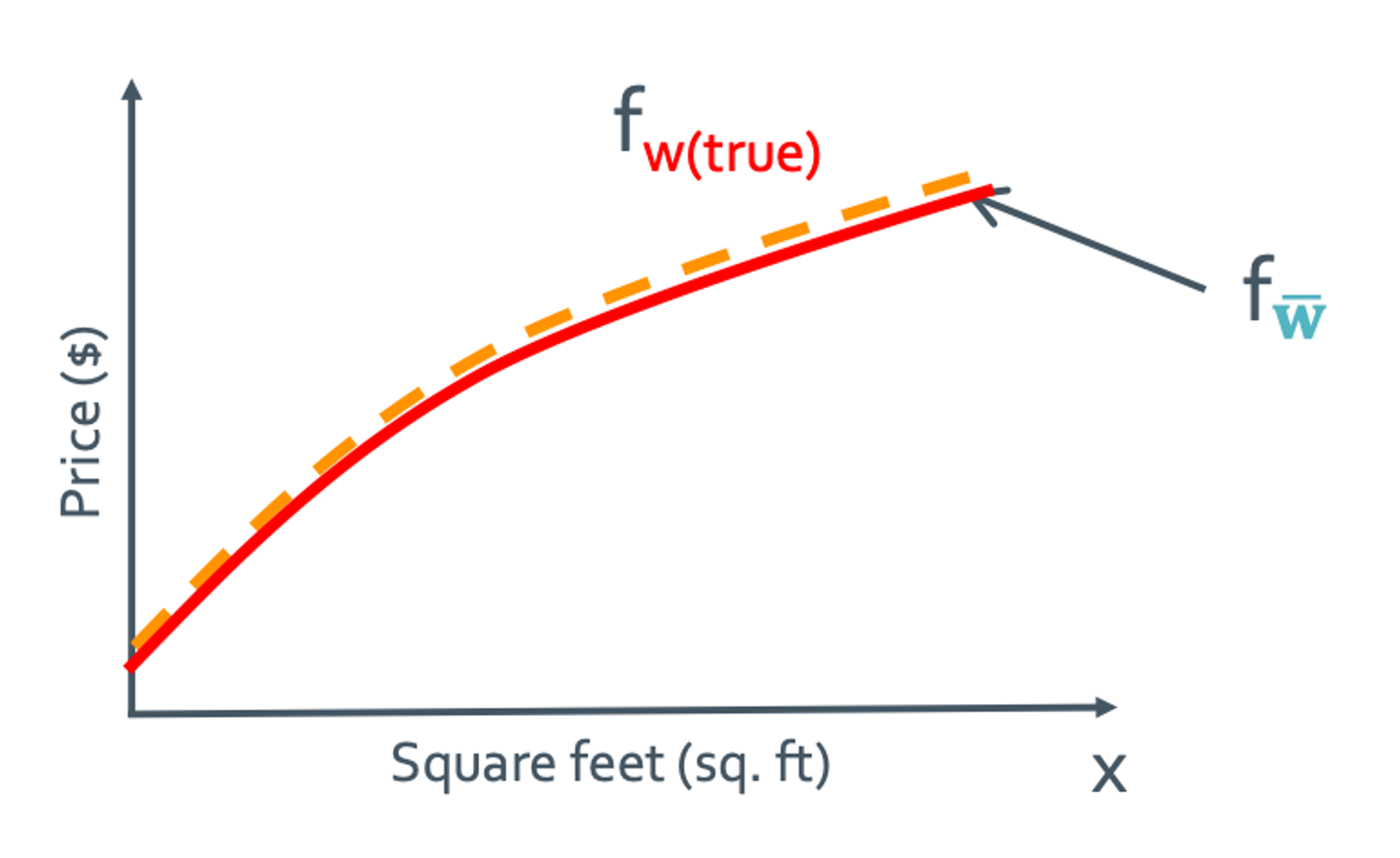
그래프가 거의 일치하므로 complexity가 높으면 bias가 낮고 variance가 높다는 것이다.

Bias-variance tradeoff

그래서 여기서 알 수 있는 것은 bias와 variance는 서로 반비례 관계에 있음을 알수 있다. 그래서 그래프로 그려보면 다음과 같이 되는 것을 확인할 수 있다.

🕷️🕸️


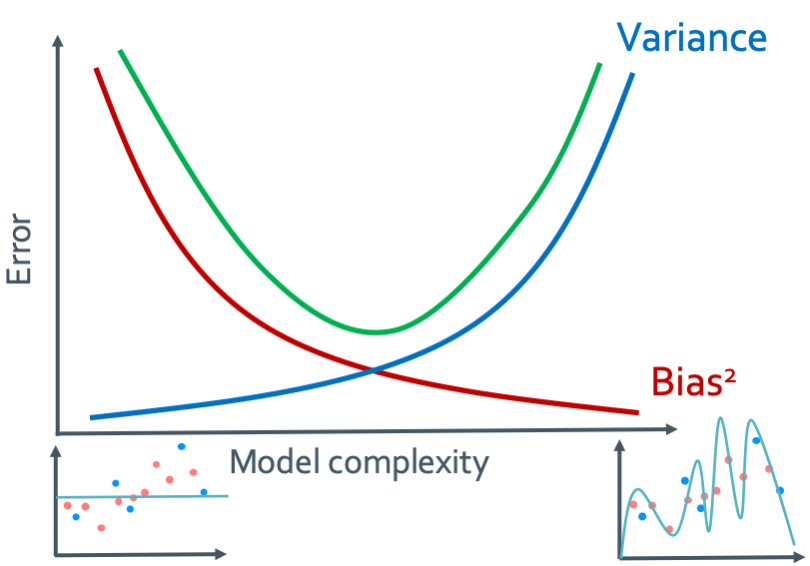
이것은 매우 중요하다. 그런데 대체 어디서 갑자기 $Bias^2$이 나온 것일까?

◼︎ Why 3 sources of error? A formal derivation

Expected prediction error = $E_{train}$ [generalization error of $\hat{w}(train)$]

averaging over all training sets and parameters fit on a specific training set

Deriving expected prediction error

  • Expected predicion error
    = $E_{train}$[generalization error of $\hat{w}(train)$]
    = $E_{train}[E_{x, y}[L(y, f_{\hat{w}}(x))]]$

    한번에 이것을 계산하는 것은 어려우니 차근차근 해 볼것이다.

    1. $x_{t}$일때 부터 해보고
    2. $L(y, f_{\hat{w}}(x)) = (y -f_{\hat{w}}(x))^2$ 를 가정할 것이다.(이게 L2-norm이다.)

• Expected predicion error at $x_{t}$

= $E_{train,yt}[(y_t -f_{\hat{w}}(x_t))^2]$

= $E_{train,yt}[(y_t -f_{\hat{w}(train)}(x_t))^2]$

= $E_{train,yt}[[(y_t-f_{w(true)}(x_t))+(f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t))]^2]$

\begin{equation} = E_{train,yt}[y_t-f_{w(true)}(x_t)]^2 \end{equation} \begin{equation} + 2E_{train,yt}[(y_t-f_{w(true)}(x_t))(f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t))] \end{equation} \begin{equation} + E_{train,yt}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2 \end{equation}

일단 하나하나씩 보자. (1)번 부터 볼것이다.

$E_{train,yt}[y_t-f_{w(true)}(x_t)]^2$
= $E_{yt}[(y_t -f_{\hat{w}}(x_t))^2]$ ($\because f_{w(true)}$와 $y_t$가 training data에 관한 함수가 아니기 때문에)

= $E_{yt}(\epsilon^2)$ ($\because y = f + \epsilon$, $epsilon$: noise )

\begin{equation} = E_{yt}(\epsilon^2) \end{equation}

그 다음은 (2)번 이다.

$2E_{train,yt}[(y_t-f_{w(true)}(x_t))(f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t))]$
= $2E_{train,yt}[\epsilon(f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t))]$ ($\because y_t-f_{w(true)}(x_t) = \epsilon$)

= $2E_{train,yt}[\epsilon] \times E_{train,yt}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]$ ($\because$ independent)

= $2E_{yt}[\epsilon] \times E_{train,yt}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]$

= 0 ($\because E_{yt}[\epsilon] = 0$이라고 가정했었음)

\begin{equation} = 0 \end{equation}

마지막으로 (3)번 이다.

$E_{train,yt}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2$
= $E_{train}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2$ ($\because f_{w(true)}$가 $y_t$에 관한 함수가 아니기 때문에)

\begin{equation} = E_{train}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2 \end{equation}

그러면 결론적으로 (1) + (2) + (3)은

$E_{yt}(\epsilon^2) + E_{train}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2$

= $[E_{yt}(\epsilon^2) - E_{yt}(\epsilon)^2]+ E_{train}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2$ ($\because E_{yt}(\epsilon) = 0$)

= $var(\epsilon)+ E_{train}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2$

= $\sigma^2 + MSE[f_{w(true)}(x_t)]$ ($\because var(\epsilon) = \sigma^2$)

가 된다. 이제 여기서 $MSE[f_{w(true)}(x_t)]$를 뜯어볼꺼다.

$MSE[f_{w(true)}(x_t)]$

= $E_{train}[f_{w(true)}(x_t)-f_{\hat{w}(train)}(x_t)]^2$

= $E_{train}[[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)] + [f_{\bar{w}}(x_t)-f_{\hat{w}(train)}(x_t)]]^2$ ($f_{\bar{w}}(x_t) = E_{train}[f_{w(train)}(x_t)]$)

\begin{equation} = E_{train}[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)]^2 \end{equation} \begin{equation} + 2E_{train}[(f_{w(true)}(x_t)-f_{\bar{w}}(x_t))(f_{\bar{w}}(x_t)-f_{\hat{w}(train)}(x_t))] \end{equation} \begin{equation} + E_{train}[f_{\bar{w}}(x_t)-f_{\hat{w}(train)}(x_t)]^2 \end{equation}

이것도 순서대로 해보자. (7)번 부터 볼것이다.

$E_{train}[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)]^2$
= $[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)]^2$ ($\because [f_{w(true)}(x_t)-f_{\bar{w}}(x_t)]$ is constant)

\begin{equation} = [f_{w(true)}(x_t)-f_{\bar{w}}(x_t)]^2 \end{equation}

그 다음은 (8)번 이다.

$2E_{train}[(f_{w(true)}(x_t)-f_{\bar{w}}(x_t))(f_{\bar{w}}(x_t)-f_{\hat{w}(train)}(x_t))]$
= $2[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)]E_{train}[f_{\bar{w}}(x_t)-f_{\hat{w}(train)}(x_t)]$

= $2[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)][E_{train}[f_{\bar{w}}(x_t)]-E_{train}[f_{\hat{w}(train)}(x_t)]]$

= $2[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)][f_{\bar{w}}(x_t)-f_{\bar{w}}(x_t)]$ ($\because f_{\hat{w}(train)}(x_t) = f_{\bar{w}}(x_t)$)

= 0

\begin{equation} = 0 \end{equation}

마지막으로 (9)번 이다.

$E_{train}[f_{\bar{w}}(x_t)-f_{\hat{w}(train)}(x_t)]^2$
= $E_{train}[f_{\hat{w}(train)}(x_t) - f_{\bar{w}}(x_t)]^2$

\begin{equation} = E_{train}[f_{\hat{w}(train)}(x_t) - f_{\bar{w}}(x_t)]^2 \end{equation}

그러면 결론적으로 (7) + (8) + (9)은

$[f_{w(true)}(x_t)-f_{\bar{w}}(x_t)]^2 + E_{train}[f_{\hat{w}(train)}(x_t) - f_{\bar{w}}(x_t)]^2$

= $[Bias(f_{\hat{w}}(x_t))]^2 + var(f_{\hat{w}(train)}(x_t))$
($\because f_{\bar{w}}(x_t) = E[f_{\hat{w}(train)}(x_t)]$)

($Var[X] = E[(X-\mu)^2] = E[X^2] - E[x]^2 = E[X^2] - \mu^2$)


가 된다. 그럼 최종적으로,

Expected prediction error at $x_t$
= $\sigma^2 + MSE[f_{w(true)}(x_t)]$
= $\sigma^2 + [Bias(f_{\hat{w}}(x_t))]^2 + var(f_{\hat{w}(train)}(x_t))$


여기에서 왜 3가지 요소가 있고 또 $bias^2$ 이었는지를 알 수 있다.

You may also enjoy

CA - chapter 5 Large and Fast: Exploiting Memory Hierarchy

9 minute read

이제 우리는 전체적인 CPU의 구조에 대해 이해할 수 있게 됐다. 그런데 우리가 자세히 다루지 않고 계속 사용하던 것이 있다. 바로 memory이다. gate나 mux등을 통해 많은 것을 만들 수 있지만 저장공간에 대한것은 아무 설명 없이 그냥 사용했다. 이번 장에는 이 memor...

Moment 2 - Review of 2024

2 minute read

열심히 블로그 쓴다고 한지 거의 4달만에 글을 다시 씁니다. 이거 굉장히 귀찮긴 하네요;;; 벌써 2025년이 돼서 개강도 했는데 이제야 24년 사진들을을 올려볼까 합니다. 24년은 제 인생에서 제일 행복한 해였던것 같습니다. 입시에서 벗어났다는 해방감도 있고 작년에 정말 많은...

ES - Week2

less than 1 minute read

https://nbviewer.jupyter.org/github/coolstone2000/coolstone2000.github.io/blob/2edbb9f3fc55fbfd2bba247b27114aaab578b5ad/files/2022142255%EC%A0%95%EC%84%9D%EC...