ML - Lecture 3: Linear regression part 1
◼︎ Linear regression
regression(회귀): 변수들 사이에서 나타나는 경향성을 설명하는 것
일단 진행하다 보면 무조건 평균으로 회귀를 한다는 것인데 왜그런진 모른다. 그냥 그런거다.
The model
일단 집값 예측 모델로 예시를 들어 설명할 것이다.
우선 어떤 model이든 data를 이용하여 만들게 되는데 input x에는 거의 y에 뭔가 영향을 미치는 feature를 넣고 output y는 우리가 궁금해 하는 것의 수치이다.
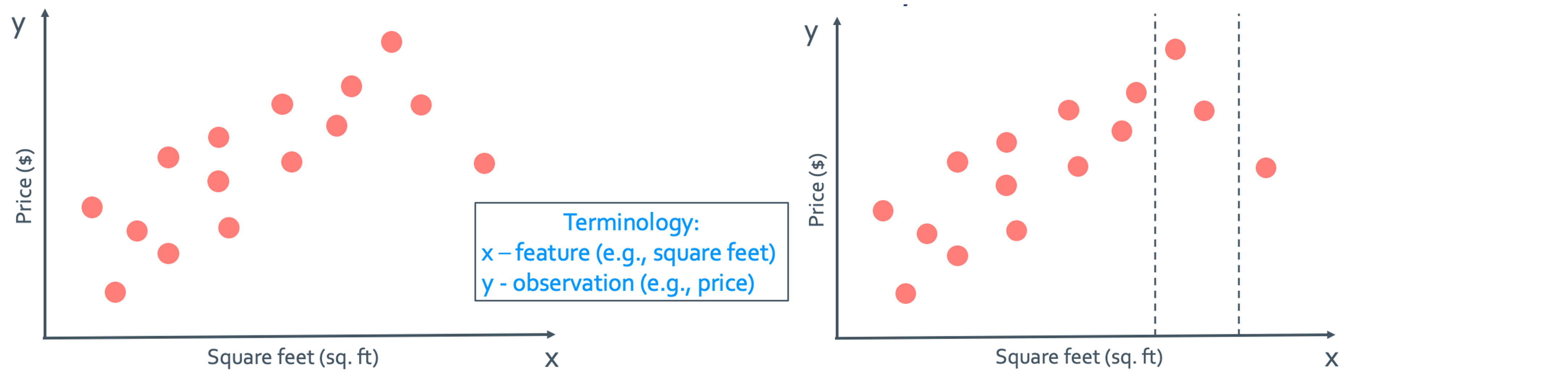
이렇게 data들을 점으로 표시해 내가 해당되는 근처의 range만 뽑아서 그 근처의 값으로만 y 값을 추정하게 되면 아주 많은 data를 모은것에 비해 실제 사용한 data는 굉장히 적다.
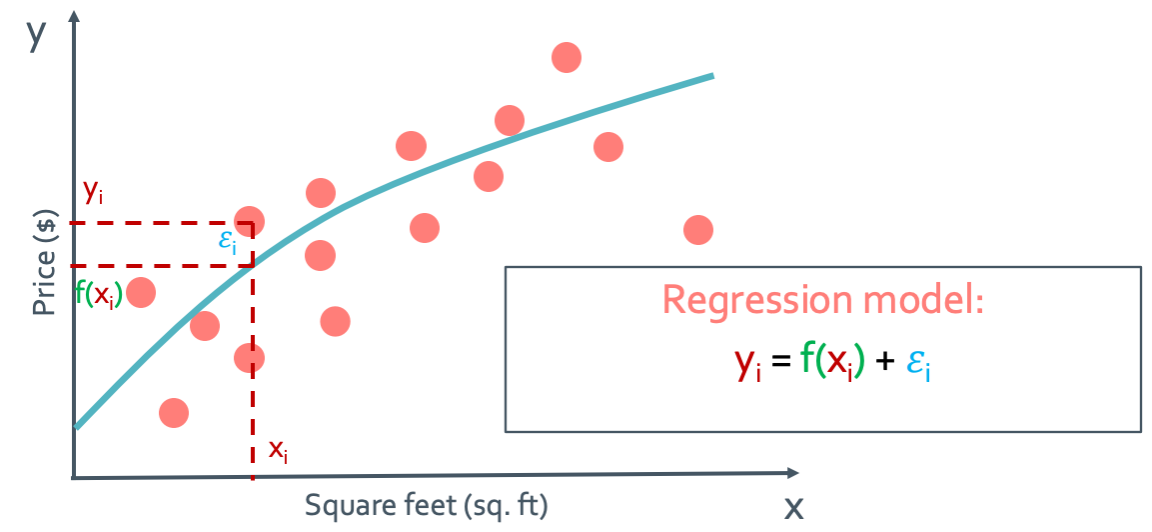
그래서 우리는 위와 같은 regression model을 사용하는 것이다.
- Machine learning flowchart
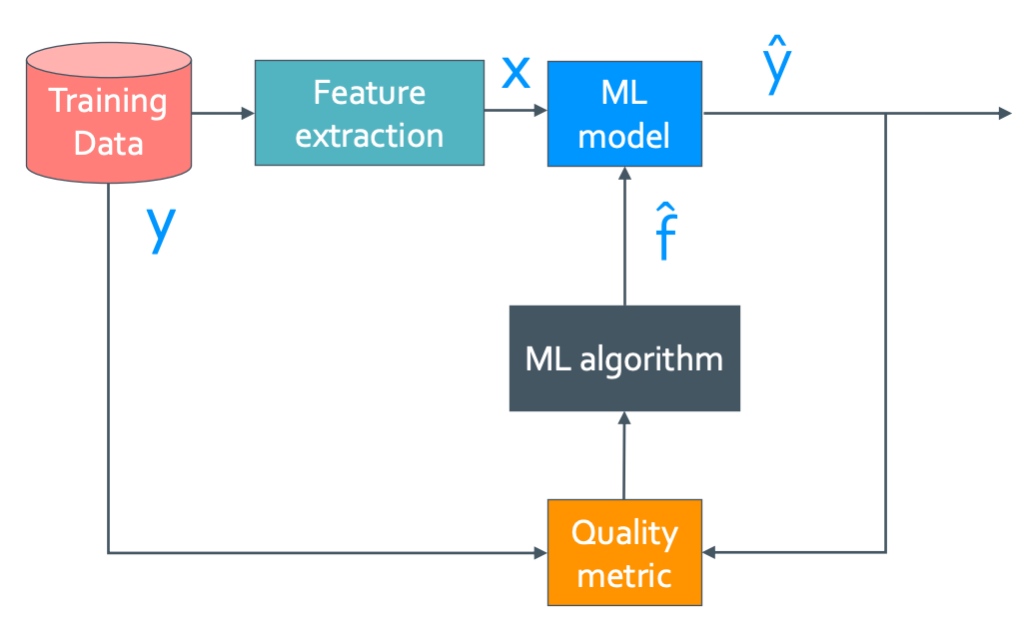
위의 flowchart는 근본적인 machine learning에 대한 것이다. 설명을 하자면 우선 Training data에서 y값에 영향을 줄만한 feature들을 뽑아 x로 만들어 준다. 그 뽑은 data들로 machine learning model을 만들게 된다. 하지만 이 model이 무조건 좋은 모델인지는 모른다. 그래서 이것을 신뢰도를 높이기 위해 Quality metric이란 것을 하여 model을 약간씩 수정하게 된다. Quality metric은 거리를 잰다는 것인데 즉 ML model이 충분히 좋아질 때 까지 $\hat{f}$를 찾는 것이다. 이것은 y와 $\hat{y}$을 비교하여 찾고 계속 update해서 오차를 점점 줄여나가는 것이다. 이것이 모든 machine learning의 기초 개념이다.
◼︎ simple linear regressinon model
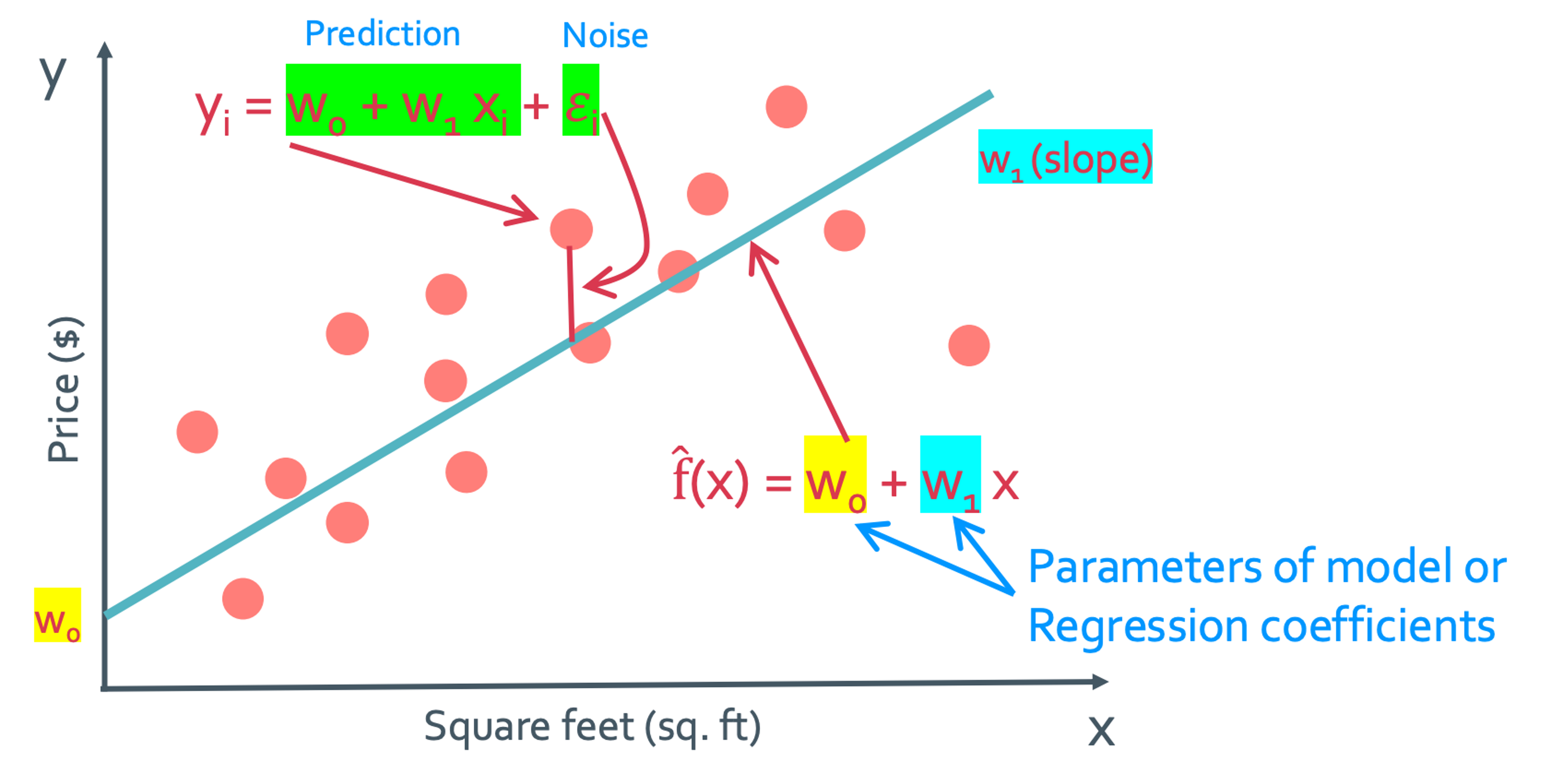
우리가 평소에 그래프를 해석하거나 찾을 때는 x나 y에 대해서 관심있고 궁금해하였다. 하지만 ML에서는 다른곳에 관심을 가져야 한다. 바로 여기서 w로 된 값들이다. 이 w로 된 값들을 parameter of model 이나 regression coefficient라고 한다. 어짜피 x와 y값은 연속적으로 다 구할 수 있고 그래프의 모양은 오히려 이 계수들에 의해 결정되게 된다. 그래서 우리는 w를 잘 찾는 것에 대해 관심을 가져야 한다. 이렇게 model을 하나 만들었다고 하면 그 x지점에서 model과 실제 data값의 차이가 생기게 될 것이다. 이는 noise($\epsilon_i$)라고 한다. 그래서 위의 flowchart에서 $\hat{f}$를 찾는 것이라고 하였는데 이제 우리는 이$\hat{f}$을 $\hat{w}$로 나타낼 것이다.
Cost
일단 noise($\epsilon_i$)가 작은 line을 찾았다면 그 line은 경향을 잘 보여주는 라인이라고 할 수 있지 않을까? 그래서 이 noise를 cost라고 한다. 이 cost를 최대한 줄일 수 있는 w를 찾아야 하는 것이다.
RSS
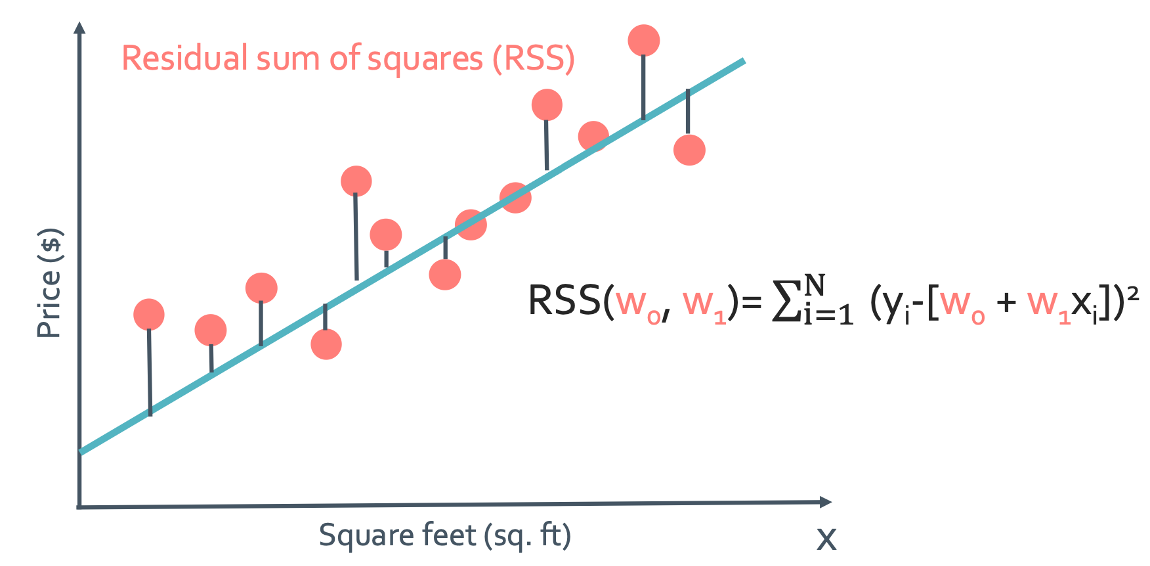
이 cost를 최대한 줄일 수 있는 w를 찾기위해 Residual sum of squares(RSS)를 사용하게 된다. (residual은 차이를 뜻한다)
$RSS(w_{0}, w_{1}) = \sum_{i=1}^{N}(y_{i}-[w_{0}+w_{1}x_{1}])^2 = \sum_{i=1}^{N}\hat{y_{i}}^2$
이 RSS가 quality metric이 되는 것이고 이 식이 알려주는 것은 어떤 함수와 데이터의 차이를 제곱한 것들의 합이 제일 작으면 cost가 좋은 함수를 찾았다는 것인데 이 것을 parameter이 w를 바꿔가며 찾는 것이다. 다시 말하자면 함수를 찾고 RSS가 작은지 확인하는게 아니라 연속적인 w의 변화를 통해 best line을 찾아내는 것이다.
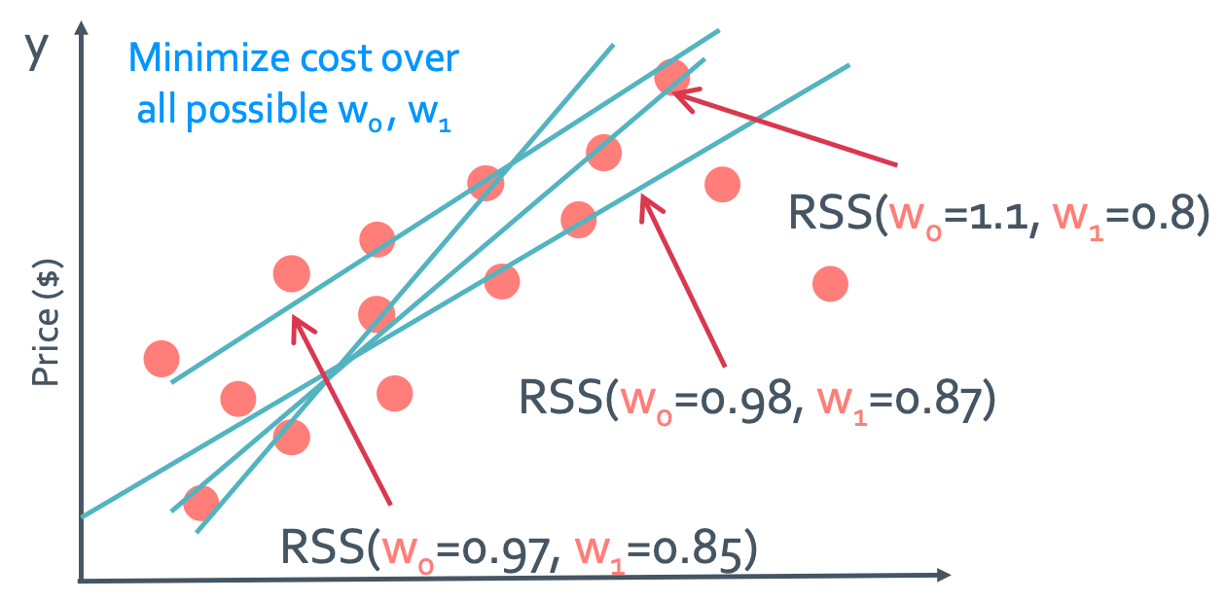
◼︎ Minimizing the cost
이 RSS값중에서 작은것을 찾는것이 문제라고 하였다. 아래에서는 이 작은 RSS값을 만드는 w를 찾는 방법에 대해 알아볼 것이다. 그래서 앞에서 배운 것을 이용해보려고 한다.

우선 가능한 모든 w들로 그래프를 그리면 이렇게 될 것이다. 이 tangent plane을 objective function, cost function, 혹은 loss function이라고 한다.
우리의 목적은 $min \sum_{i=1}^{N}(y_{i}-[w_{0}+w_{1}x_{1}])^2$이 되는 $w_{0}, w_{1}$을 찾는 것이다.
앞에서 배운 표현을 이용하면 $\hat{w_{0}}, \hat{w_{1}} = argmin\;RSS(w_{0}, w_{1})$을 구하면 된다. 이걸 이용해 $\hat{w_{0}}, \hat{w_{1}}$를 찾는 것을 학습이라고 한다.
Approach 1: Set gradient 0
Gradient가 0인 지점을 찾으면 local minimum일 것이니까 꽤나 정확한 방법일 것이다. 그런데 문제점으로는 거의 모든 ML problem은 gradient = 0 을 가지지 않고 만에 하나 존재 하더라도 정말 구하는 계산량이 어마무시하다. 그래서 우리는 이 방법을 사용하지 않는다.
Approach 2: Follow the slope
이 방법은 눈을 감고 산에서 내려가는 것과 같다. 대신 경사가 급한쪽으로 계속 내려가는 것이다. 그러면 언젠가는 어느 방향으로 가도 거의 평평한 지점에 도착하지 않겠는가? 이것이 바로 2번째 방법이다.
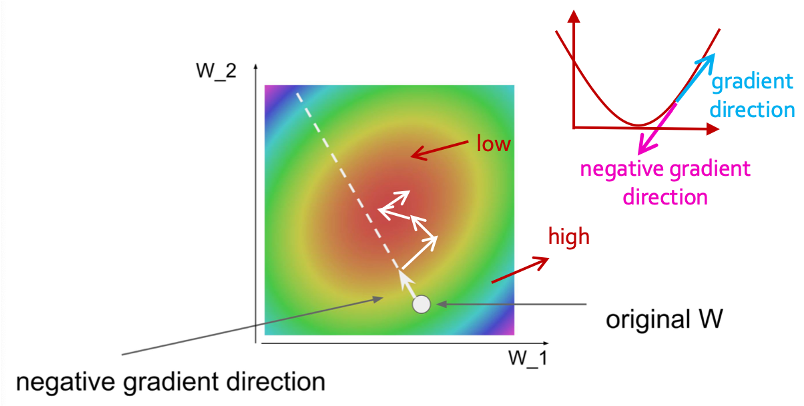
이 그림을 보면 negative gradient direction으로 점점 움직이면서 high에서 low로 가는 것을 확인할 수 있다.
이제 경사가 급한쪽 반대로 가야한다는 방향을 알게되었다. 그런데 얼마나 가야하는지에 대해서는 아직 다루지를 않았다. 이 얼마나 가냐는 step size(learning rate)라고 한다. 이것과 convergence criteria를 이용해 알고리즘을 짜게 된다.
While not converged, $w^{t+1} \leftarrow w^{t} - \eta \bigtriangledown RSS(w^{t}) \Rightarrow \hat{w}$
- $\eta$: stepsize(learning rate)
Choosing stepsize: Fixed stepsize
이렇게 stepsize를 정하는 것을 Learning rate scheduling이라고도 한다. 그 중 fixed stepsize 방법은 항상 간격이 같게 움직이는 것이다.
Choosing stepsize: Decreasing stepsize
Decreasing stepsize 방법은 learning rate decay라고 한다. 이 것은 처음엔 과감하게가다가 뒤로 갈수록 점점 조심스러워지는 것이라고 생각하면 된다. 즉, stepsize가 점점 감소하는 것이다. 다음은 흔히 stepsize로 사용하는 것들이다
- $\eta_{t} = \frac{\alpha}{t}$
- $\eta_{t} = \frac{\alpha}{\sqrt{t}}$
Convergence criteria
Convex function(아래로 볼록인 함수)일 때는 optimum하게 $\triangledown RSS(w) = 0$ 이 되지만, 실제로는 그런 함수라는 보장이 없기 때문에 $||\triangledown RSS(w)|| < \epsilon $ ($\epsilon$: small threshold)를 만족하는 순간 멈추면 된다. 0이 아니어도 충분히 작은 숫자이기 때문에 멈춰도 된다. 왜냐하면 실제 결과는 큰차이가 없기 때문이다.
The fitted line: use + interpretation
- Fitted line: $\hat{f}(x) = \hat{w_{0}} + \hat{w_{1}}x$
- Regression model: $y_{i} = \hat{w_{0}} + \hat{w_{1}}x_{i} + \epsilon_{i}$
- Estimated parameters: $\hat{w_{0}}, \hat{w_{1}}$
Coefficient를 해석하면 다음과 같다.
- Intercept(절편): $\hat{w_{0}}$
- Slope(기울기): $\hat{w_{1}}$
◼︎ Adding higher order(더 높은 차수)
지금까지는 2개의 paramter만 봐서 직선의 regression function만 보았다. 그런데 차수만 높이면 다음과 같은것도 가능하지 않나?
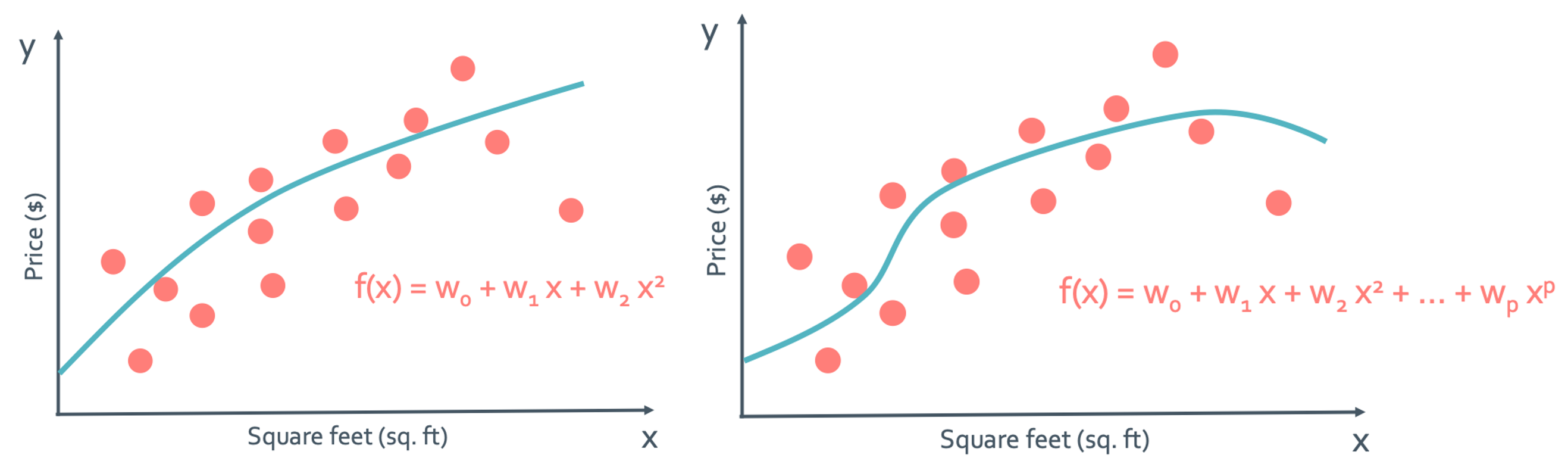
왼쪽은 quadratic(이차)이고 오른쪽은 polynomial(다항) 함수의 그래프이다. 그럼 이렇게 w의 parameter만 늘리면 polynomial regression을 할 수 있게 된다.
Model: $y_{i} = w_{0}+w_{1}x_{i}+w_{2}x_{i}^2+...+w_{p}x_{i}^p + \epsilon_{i}$
- features: $1, x, x^2, …,x^p$(Non-linear feature)
- parameter: $w_{0}, w_{1}, …, w_{p}$
근데 앞에서도 말했듯이 여기서 x나 y는 변수로 보는게 아니다. 그렇기 때문에 이 방정식은 polynomial funcion꼴이지만 “w에 대해 linear regression”이다. 즉, Non-linear feature를 가지는 linear regression인 것이다.
◼︎ Detrending time series
이게 무슨 뜻일까? 시간 추세를 억제하다? 흠… 다음의 예시를 봐보자.
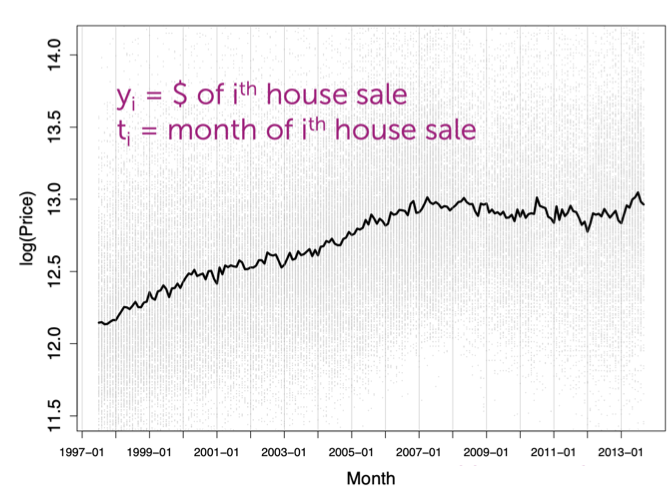
여름일땐 집이 잘팔리고 겨울일때는 집이 안팔리는 뭔가 그러한 경향(trend)가 관측이 된다. 이런 경향은 regression모델을 오히려 복잡하게만 만들지 않을까?
그래서 이것을 detrending해버리겠다는 것이다.
Model: $y_{i} = w_{0}+w_{1}x_{i}+w_{2}sin(\frac{2\pi t_{i}}{12}-\phi) + \epsilon_{i}$
모델이 다음과 같다고 생각하자. 그러면 $w_{0}+w_{1}x_{i}$이 부분은 linear trend
라고 할 수 있고 $w_{2}sin(\frac{2\pi t_{i}}{12}-\phi)$은 seasonal component라고 할 수 있을 것이다.
그리고 $\epsilon_{i}$은 known phase혹은 shift라고 한다.
삼각함수 법칙에 의하면 $w_{2}sin(\frac{2\pi t_{i}}{12}-\phi)= w_{2}sin(\frac{2\pi t_{i}}{12})cos(\phi) - w_{2}cos(\frac{2\pi t_{i}}{12})sin(\phi)$가 된다.
그럼 이걸 $w_{2}sin(\frac{2\pi t_{i}}{12})+w_{3}cos(\frac{2\pi t_{i}}{12})$라고 써도 되는거 아닌가?
Model: $y_{i} = w_{0}+w_{1}x_{i}+w_{2}sin(\frac{2\pi t_{i}}{12}) + +w_{3}cos(\frac{2\pi t_{i}}{12}) + \epsilon_{i}$
이것은 최종적인 식이다.
- Global trend: $w_{0}+w_{1}x_{i}$
- Local trend: $w_{2}sin(\frac{2\pi t_{i}}{12}) + +w_{3}cos(\frac{2\pi t_{i}}{12})$
약간 전회의 small signal 개념이 생각난다. 전회에선 오히려 small signal에 더 관심을 가지지만 여기선 반대로 detrending시킬 생각을 한다.
Generic basic expansion
Model: $y_{i} = w_{0}h_{0}(x_{i})+w_{1}xh_{1}(x_{i})+w_{2}h_{2}(x_{i})+...+w_{D}h_{D}(x_{i}) + \epsilon_{i} = \sum_{j=0}^D w_{j}h_{j}(x_{i}) + \epsilon_{i}$
◼︎ Adding other inputs
이제 요소를 더 늘려볼까 한다. 즉, scalar 값이었던 input을 이제 vector로 표현해보겠다.
Genral notation
- Output: y (scalar)
- Input: x = (x[1], x[2], …, x[d]) (d-dim vector)
Notational conventions:
- $x[j] = j^{th}$ input (scalar)
- $h_{j}(x) = j^{th}$ feature (scalar)
- $x_{i}$ = input of $i^{th}$ data point (vector)
- $x_{i}[j] = j^{th}$ input of $i^{th}$ data point (scalar)
Model: $y_{i} = w_{0}h_{0}(x_{i})+w_{1}xh_{1}(x_{i})+w_{2}h_{2}(x_{i})+...+w_{D}h_{D}(x_{i}) + \epsilon_{i} = \sum_{j=0}^D w_{j}h_{j}(x_{i}) + \epsilon_{i}$
그래서 이 수식에서 $x_{i}$는 벡터 형태의 input, w들은 regression coefficient, 그리고 $w_{j}h_{j}(x_{i})$는 feature extractor라고 하는 것이다.
◼︎ Fitting the linear regression model
Step 1: Rewrite the regression model

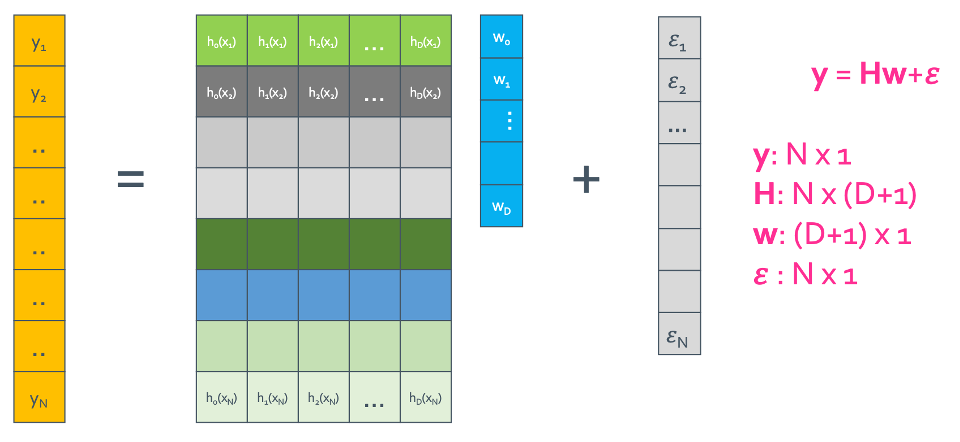
Step 2: Compute the cost
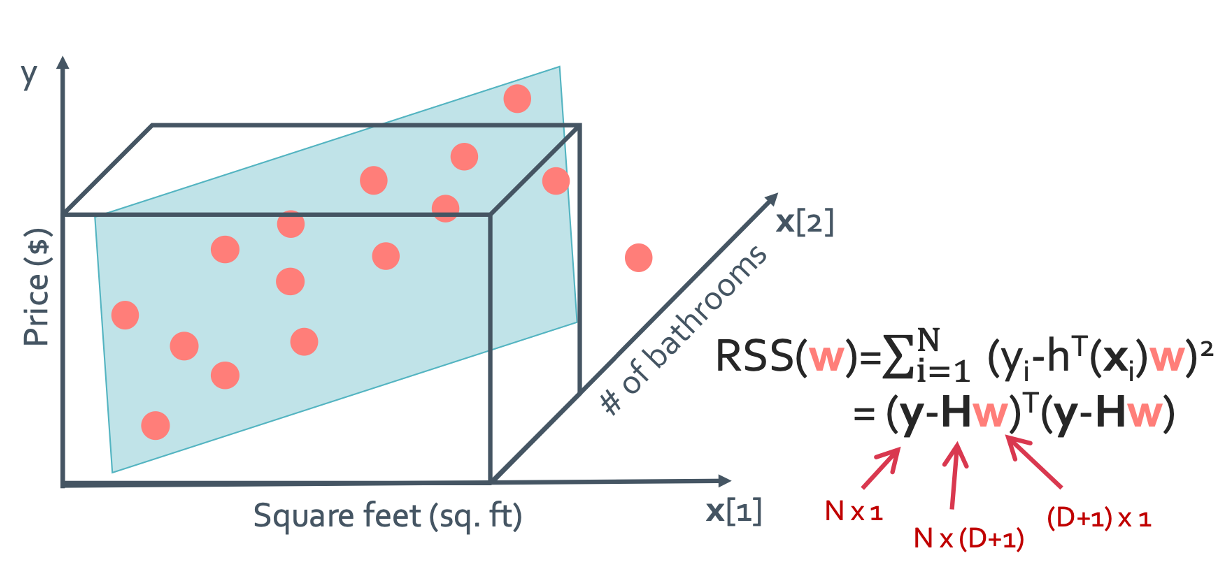
Step 3: Take the gradient
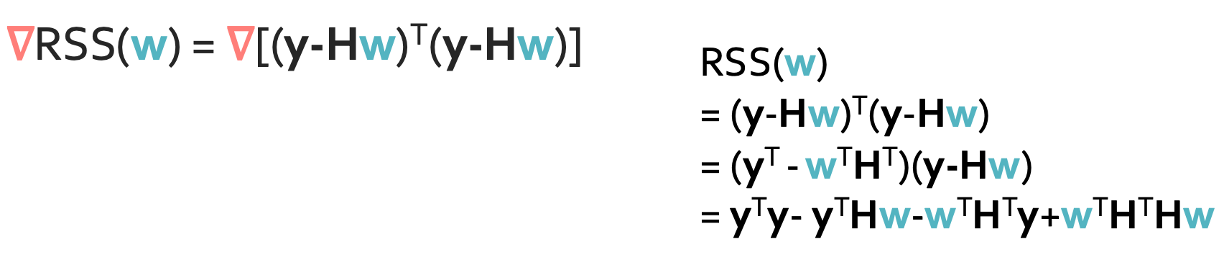
이 그래디언트 계산을 하기 위해서는 한가지 알아둬야하는 식이 있다.
그리고 행렬의 미분에서 알아야 하는것은 행렬 $w$에 대한 미분은 $w$만 지워야 하고 $w^T$에 대한 미분은 $w^T$만 지워야 한다. 이것을 적용하게되면 다음과 같은 식을 얻을 수 있다.
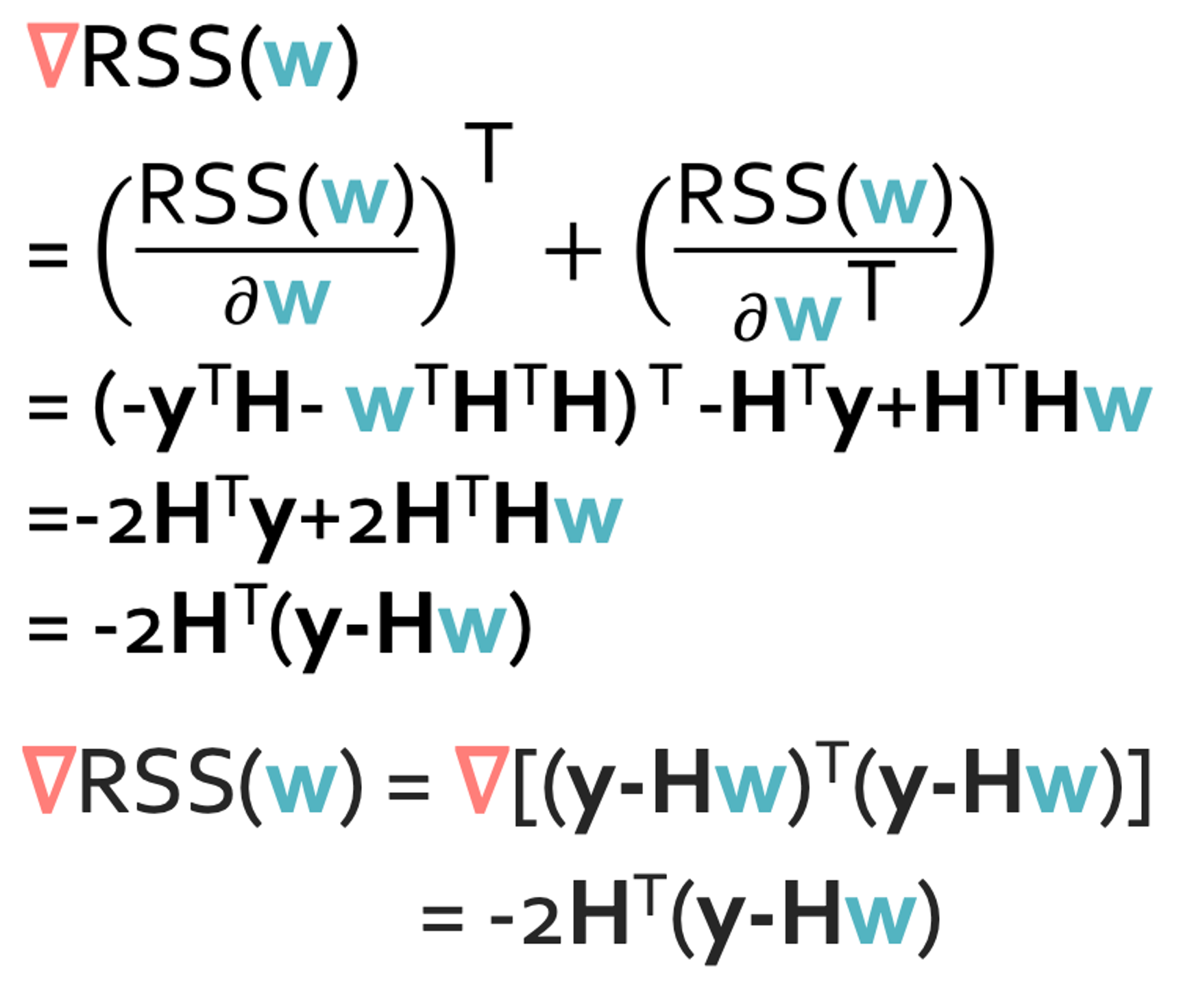
Step 4(Approach 1): Set the gradient = 0
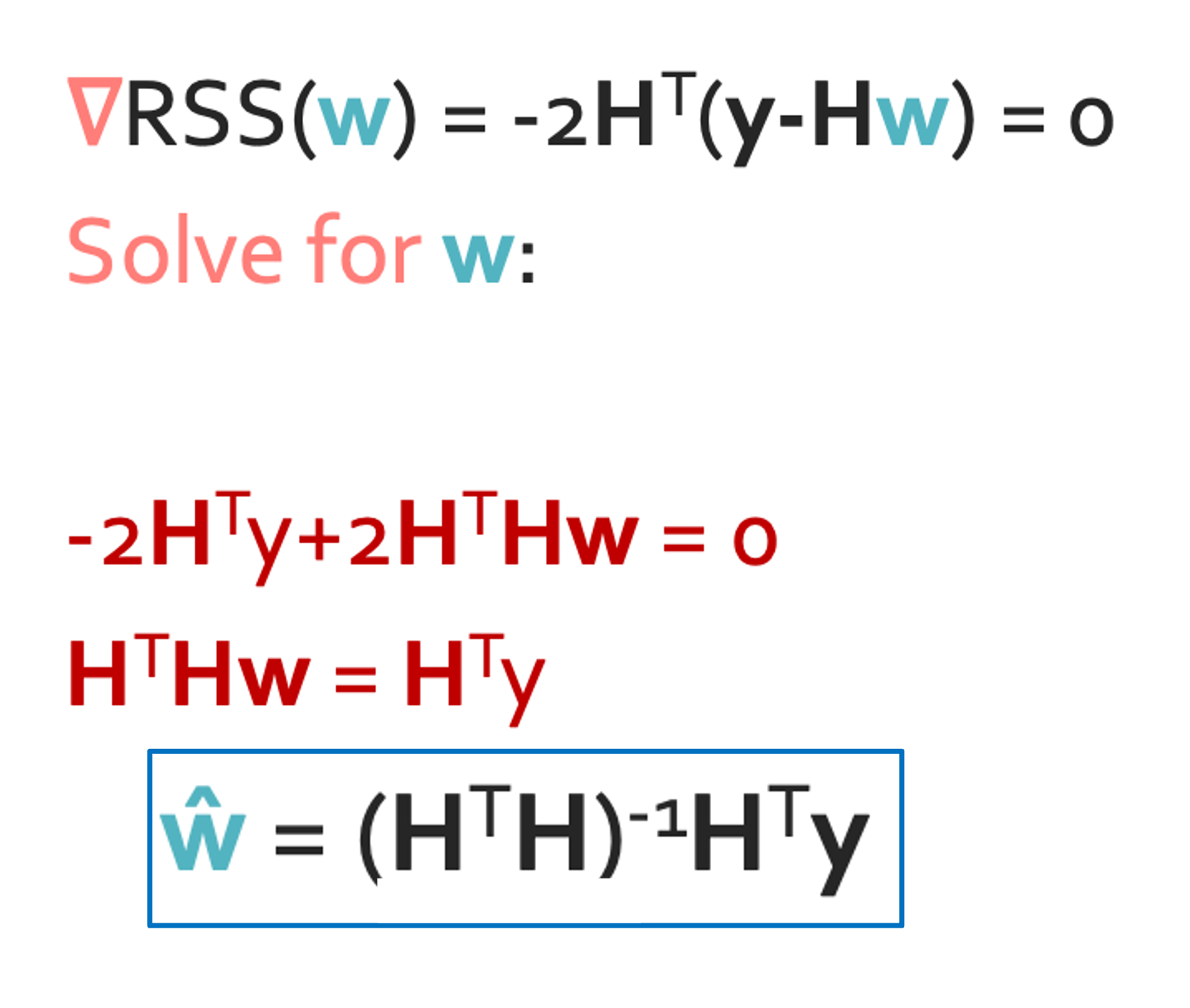
$\hat{w} = (H^{T}H)^{-1}H^{T}y$ 로 깔끔하게 나오는것 같지만 생각할 부분이 있다. 일단 역함수를 계산하려면 정방행렬이어야한다. 그것부터 쉽지 않은데 역함수 계산 자체도 원래 쉽지 않은걸 알고있지않나? Dimension이 늘어날 수록 연산량은 미친듯이 늘어나게 된다. 그래서 이렇게 구하는 것은 힘들다.
Step 4(Approach 2): Gradient descent
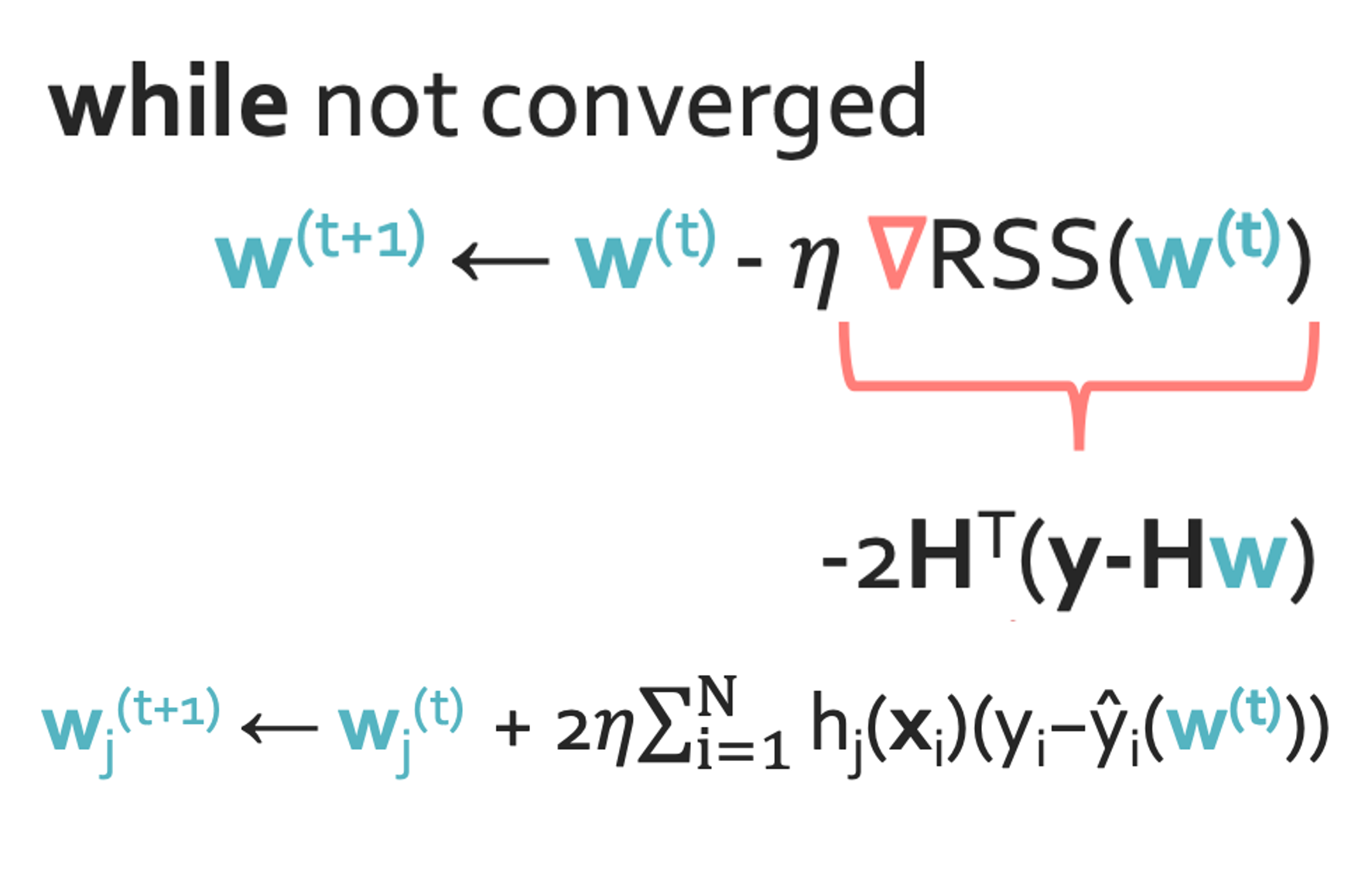
우선 여기서 $\eta > 0$이다.
그런데 분명 뭔가 - RSS가 gradient decent라고 했는데 +가 있어서 이상하다.
이것은 아래를 보면 이해가 된다.
일단 gradient decent이기 때문에
$||\triangledown RSS(w)|| < \epsilon $
을 사용할 것이다.

$-$가 서로 상쇄가 돼었기 때문에 +가 된거처럼 보이는 것이다. 그럼 이제 $\triangledown RSS(w^{(t)})$ 안에 무엇을 넣어야 하는지 알게되었다. 그런데 이 magnitude를 어떻게 처리를 해야하는 것일까? 여기에는 Norm의 개념이 쓰인다. 크기를 정의하는 방법이 여러개이기 때문이다.
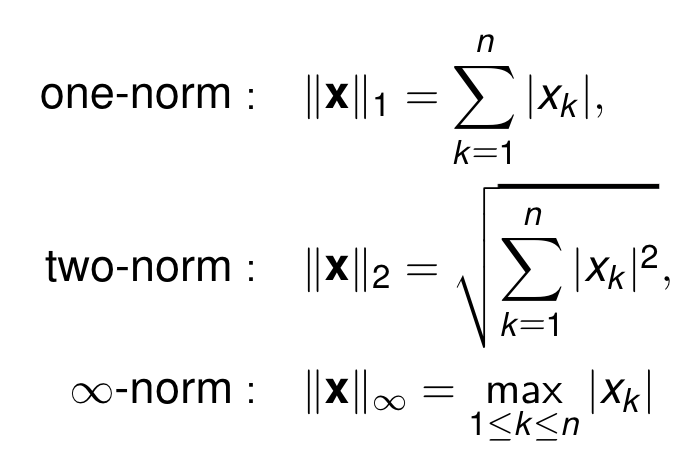
이런식으로 norm의 정의하게 되는데 이제 뒤에서 하겠지만 순서대로 L1 norm, L2 norm 이런식으로 된다. 그래서 어떤 방식을 쓰냐에 따라 조금씩 차이를 보이고 그것에 대해서도 배울 것이다.
◼︎ min RSS?
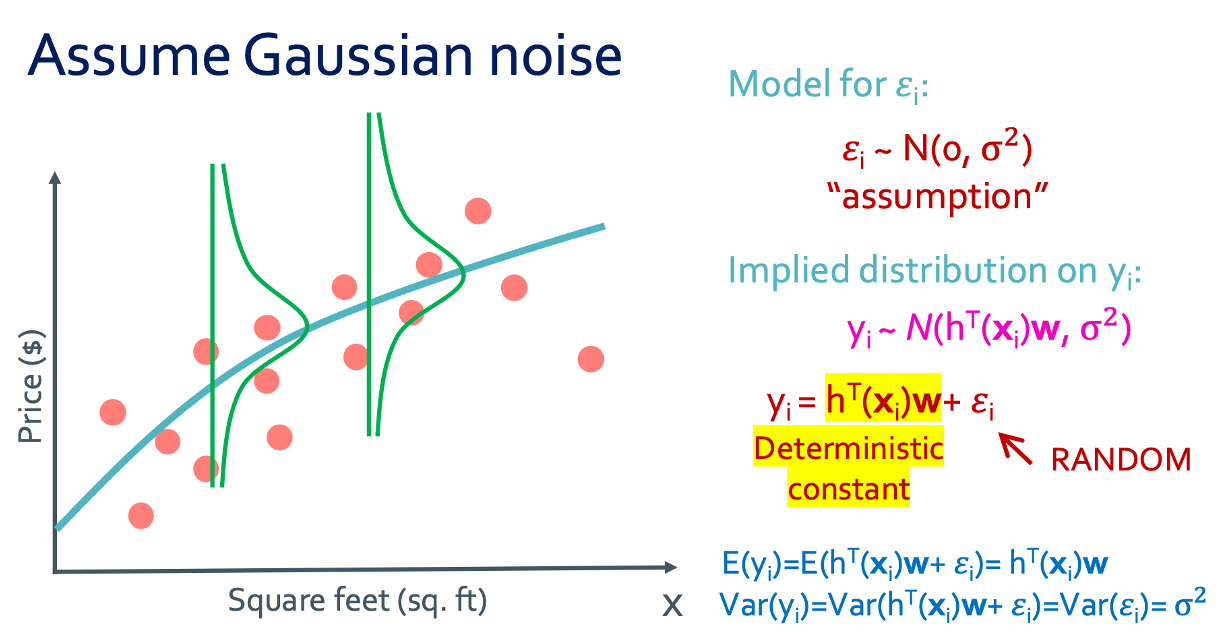
가우시안 분포로 나타내면 이런식으로 나타낼 수 있게 된다. 그러면 앞에서 했듯이 Maximum likelihood가지는 parameter들을 구하면 되었지 않았나? 그것을 해볼 것이다.

계산을 이렇게 해보면 -가 앞으로 나오게 되면서 $argmax$였던 것이 $argmin$이 되게었고 그러면 이게 RSS가 된거 아닌가?
그래서 제일 작은 RSS값을 찾는다는 것은 가우시안 노이즈 모델에서 (log)likelihood를 최대화하는 것이다.
◼︎ Numerical vs analytic gradient
- Numerical gradient: 노가다이다. approximate, slow 하지만 easy to write
- Analytic gradient: 진짜 미분하는 것이다. exact, fast 하지만 error-prone(계산 실수)
그래서 실제에서는 항상 analytic gradient를 사용하긴 한다. 그게 정확하기 때문이다. 그런데 이렇게 찾고 난 다음 확인을 하기 위해 numerical gradient로 대조를 해보게 된다. 이 과정을 gradient check라고 한다.