ML - Lecture 2: Point estimation

---

◼︎ Estimators

• 추정량
  • Point estimation: Single best prediction을 얻기 위한 시도, 단 하나의 해임
  • Bayesian learning: 확률 분포를 포함하고 있음(불확실성을 내포)
    ☞Point estimation이 확률 값 자체라면 bayesian은 분포표까지 생각하는 것

◼︎ Maximum likelihood estimation(MLE) for a Binomibal distribution

Machine learning에서 확률을 표현하는 기호로는 $\theta$로 사용한다.
만약 Head, Tail만 경우의 수가 나타나는 것으로 했을 때,

P(D|$\theta$) = $\theta^{a_H} (1-\theta)^{a_T}$
그렇다면 probability와 likelihood는 무었일까? 일단 probability(확률)은 우리에게 익숙하다. 왜냐하면 $\theta$가 주어지는 문제를 여태까지 풀어왔기 때문이다. 주사위 던지기, 가위바위보 등 확률이 이미 정해져 있지 않은가? 하지만 likelihood와 같은 경우는 모르는 $\theta$값을 찾는 것이 목적이다. 그래서 그래프가 연속적으로 그려지게 되는 것이다.

MLE : Choose $\theta$ that maximizes the likelihood of observed data (빈도가 제일 큰부분의 위치 $\theta$를 찾아냄)

$\hat{\theta}$ = arg max P(D|$\theta$) = arg max ln P(D|$\theta$)
☞ max는 말 그대로 진짜 그 함수의 최대값을 의미한다.
☞ arg max는 함수값이 최대가 되는 위치를 알려줌. $f(x)$가 최대일 때 $x$값을 리턴한다는 뜻
☞ $\hat{\theta}$ 은 보통 $\theta$ 의 추정치일 때 사용

우리가 함수의 local maximum을 찾을 때 미분값이 0이 되는 숫자를 찾는것 처럼 $\hat{\theta}$를 구할 수 있다.
$\frac{d}{d\theta}$ln P(D|$\theta$) = 0 $\to$ $\frac{a_H}{\theta} + \frac{-a_T}{1 - \theta}$ = 0
$a_H - a_H\theta - a_T\theta$ = 0, $\hat{\theta}$ = $\frac{a_H}{a_H + a_T}$

$\hat{\theta}_{MLE}$ = $\frac{a_H}{a_H + a_T}$

◼︎ Hoeffding’s Inequality (PAC, Probably Approximately Correct)

$N = a_H + a_T =$ 시행횟수인데 이게 커질수록 정확도가 올라가지 않을까?
그래서 Hoeffding’s Inequality를 이용을 하는거다.

$P(\vert \hat{\theta}_{MLE} - \theta^*\vert \geq \epsilon) \leq 2e^{-2N\epsilon^2}$

• $\theta^{*}$ :완벽한 solution
  

• $\vert\hat{\theta}_{MLE} -\theta\vert$ : errors
  

• $\epsilon$ :오차범위, 즉 N이 커질수록 점점 정확해지는 것이다.
  
  

◼︎ MLE for continuous variables(Gaussians)

• Gaussians
  $f_{\mu, \sigma^2}(x_i) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)$
  
  우선 가우시안을 learning한다는 뜻은 $\mu$와 $\sigma$를 estimate한다는 것이다. 위에서 확률 $\theta$를 추정했듯이 가우시안에서는 두 가지 요소를 이용한다.
  

• Properties of Gaussians

  1. Sum of Gaussian
     If $X→N({\mu_x},{\sigma_x^2})$ and $X→N({\mu_y},{\sigma_y^2})$, $Z = X + Y$, than $X→N({\mu_x}+{\mu_y},{\sigma_x^2}+{\sigma_y^2})$
     
  2. Multiplying of Gaussian
     $E(Y) = E(aX+b) = aE(X) + b = a{\mu} + b$
     $Var(Y) = Var(aX+b) = Var(aX) = (a^2)Var(X) = a^2{\sigma^2}$
     ${\therefore}$ $X→N({\mu},{\sigma^2})$, if $Y = aX + b, Y→N(a{\mu} + b, a^2{\sigma^2})$
     
     

그래서 MLE를 Gaussian적용하면

$P(D|\mu, \sigma) = \prod_{i=1}^{N}f_{\mu, \sigma^2}(x_i) = (\frac{1}{\sigma\sqrt{2\pi}})^N \prod_{i=1}^{N}\exp \left( -\frac{(x_i-\mu)^2}{2\sigma^2} \right)$

가 되고 log를 취한 꼴은

$ln P(D|\mu, \sigma) = -N \ln {\sigma\sqrt{2\pi}} - \sum_{i=1}^{n} \frac{(x_i-\mu)^2}{2\sigma^2}$
가 된다.

그래서 $\mu$에 대해 편미분하고 $\sigma$에 대해 편미분을 통해 0이되는 값을 찾으면

${\hat{\mu}}_{MLE} = \frac{1}{n}\sum_{i=1}^{n}x_i$ : sample mean

${\hat{\sigma}^2}_{MLE} = \frac{1}{n}\sum_{i=1}^{n}\left(x_i-\mu\right)^2$ : sample variance
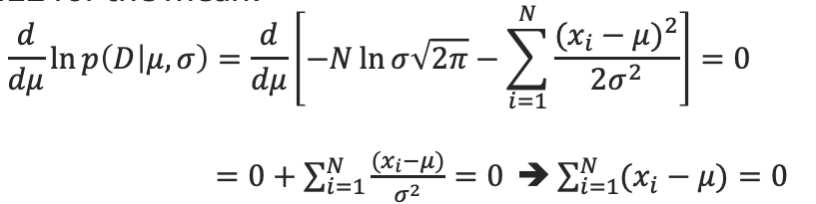
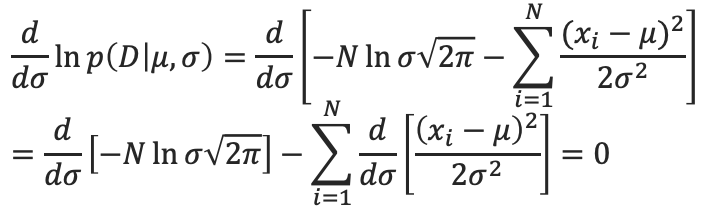
를 구할 수 있다.
이렇게 구했지만 이건 이상적인 값이라서 true parameter로 사용할 수 없다. 그래서 biased라는게 생기게 되는데 biased = Estimation - golden solution이 된다. ($Bias(X) = E(X) - X^{*}$)
만약 bias 값이 0이 되면 golden soluition을 찾아냈다는 것이고 이것을 unbiased라고 한다. 추가적으로 unbiased된 것은 다음과 같이 나타낸다. ${\hat{\sigma}^2}_{unbiased} = \frac{1}{n}\sum_{i=1}^{n-1}\left(x_i-\mu\right)^2$

재밌는 성질 중 하나는 ${\mu}$와 ${\sigma}^2$의 bais 상태가 서로 다르다는 것이다.

• MLE for the expectation of a Gaussian is unbiased

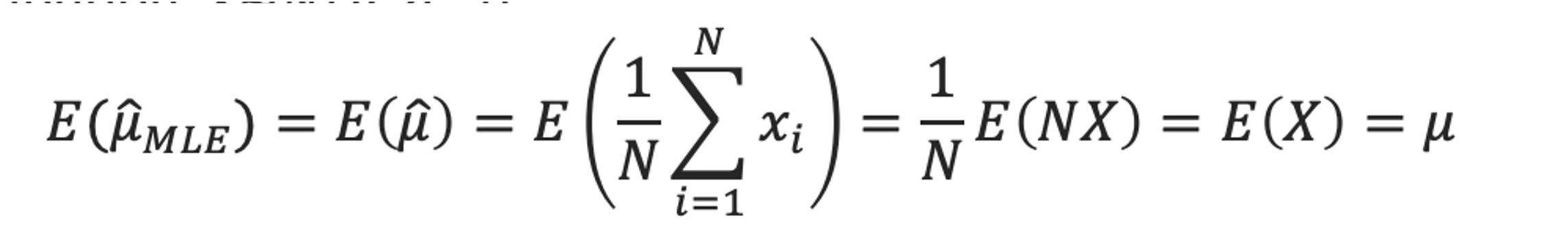
그러므로 $\hat{\mu}_{MLE}$는 unbiased이다.

• MLE for the variance of a Gaussian is biased

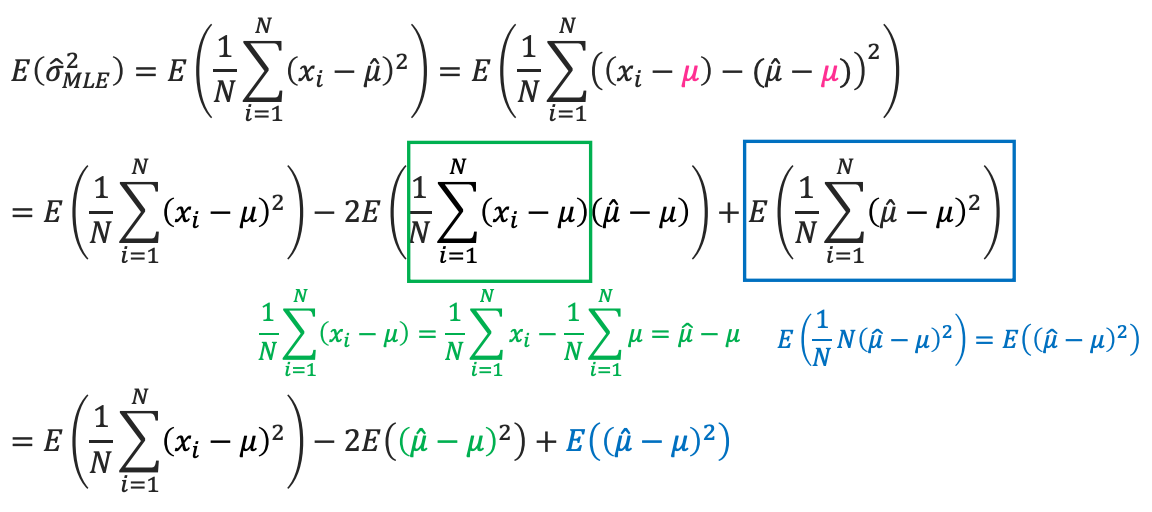
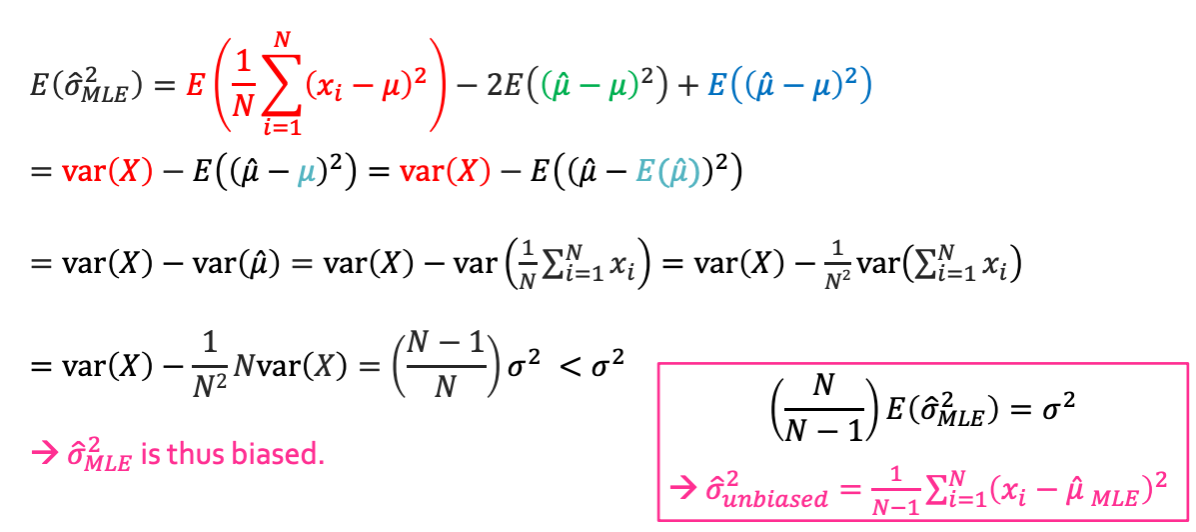
그래서 unbiased 된 variance를 찾고 싶으면 오른쪽 박스처럼 $\left(\frac{N}{N-1}\right)$을 곱해줘야 하는것이다.