ML - Lecture 19: Neural Networks part3
이제 이 neural network를 실제로 어떻게 써야할지에 대해 다뤄보자.
◼︎ Neural network in Practice: Optimization
들어봤듯이 neural network를 training 시키는 것은 굉장히 어렵다. 연산량이 엄청 많기도 하고 local & global minima의 문제 같은 것들이 있다. 일단 앞에서 배웠던 loss function을 가져와서 계산해볼까?
Optimization through gradient descent(SGD)
$\theta \leftarrow \theta - \eta \frac{\partial J(\theta)}{\partial \theta}$
이런게 있었다는게 기억 날 것이다. $\eta$는 learning rate(step) 이런식으로 정의해서 사용했다. 이게 너무 크면 우리가 구해야 하는 지점으로 못갈 수도 있고 너무 작으면 연산량이 너무 많아지는 등의 문제가 생겼다. 그래서 가면 갈수록 점점 크기가 줄어드는 방식을 택하기도 하고 그랬었다.
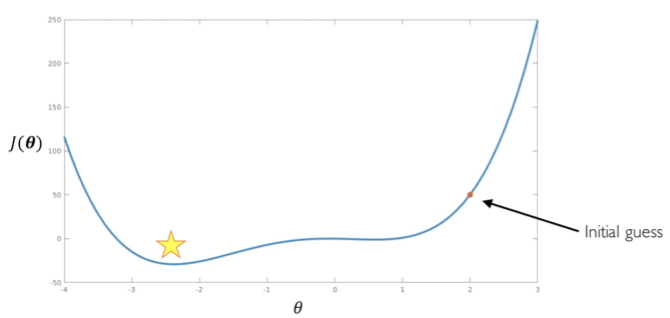
그런데 위에서 말한 모든 방법들이 local minimad나 saddle point에서 탈출하지는 못한다. 그래서 이것을 해결하기 위해 여러가지 방법을 만들었다.
Adaptive learning rates
아래와 같은 방식들이 있다.
- Momentum: 과거의 방향을 보고 결정
- Adagrad: Grad가 컸으면 작아지고, 작았으면 다시 커진다
- Adadelta
- RMSProp: Adadelta랑 비슷한거라고 했다
- Adam: 위의 방식들을 다 합쳐서 제일 많이 쓰인다
Momentum
Momentum방식을 어떻게 이용했는지 확인해보겠다. 일단 SGD와 Momentum 방식을 합쳐서 사용한다.
$v_{t+1} = \rho v_t + \nabla f(x_t), \; x_{t+1} = x_t - \eta \, v_{t+1}$
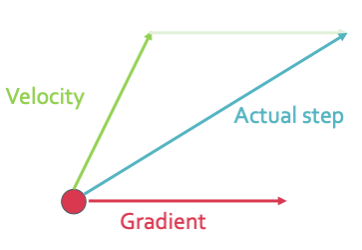
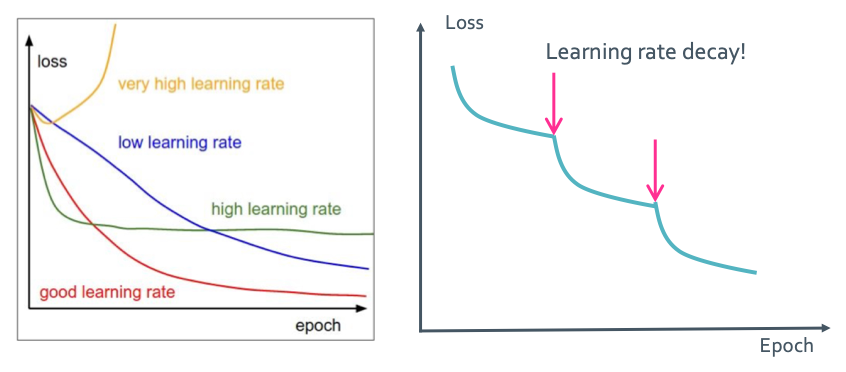
이렇게 만들어도 어떤 방식을 택하던 learning rate가 너무 커서도 작아서도 안된다는 것을 아래 그래프에서 확인할 수 있다. 그래서 앞에서 말한 점점 작아지는 방식을 통해 loss율을 줄일 수 있다. 이것을 step decay라고 한다.
- Exponential decay: $\eta = \eta_0 e^{-kt}$
- 1/t decay: $\eta = \eta_0 / (1+kt)$
이렇게 하면 아래 그림처럼 loss를 획기적으로 줄일 수 있다.
◼︎ Neural network in Practice: Mini-batches
위에서 구한것들을 이용하여 gradient descent를 하면 계산이 간단하지는 않다. 앞에서도 배웠듯 계산을 간단히 해주기 위해 stochastic gradient descent를 채택했다. 그런데 방법도 noise가 굉장히 많이 낀다는 단점이 있다. 그래서 좀더 보완한 방식인 mini-batch 방식을 사용하여 연산량을 줄일 수 있다.

◼︎ Neural network in Practice: Activation functions
Neural network에 대해 설명할 때 처음에 g의 함수를 뭐로 두냐에 따라 model을 결정 할 수 있다고 하였다. 그래서 우리가 계속 봤던 g(activation function)은 sigmoid였다.
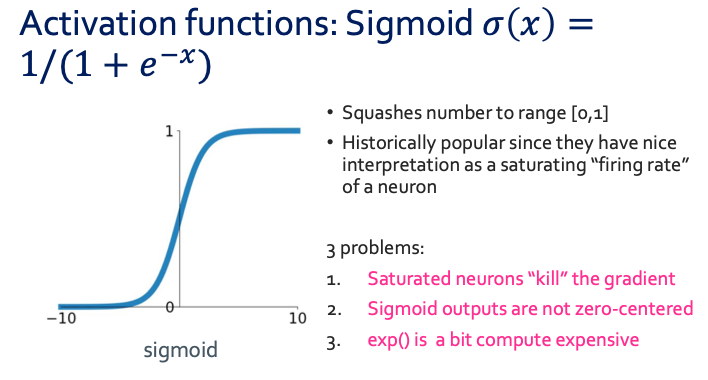
그런데 위에서 3가지의 문제점이 보이듯이 sigmoid는 좋은 activation function이 아니다. 일단 두 번째 문제부터 해결 할 수 있는 $tanh(x)$함수를 봐보겠다.
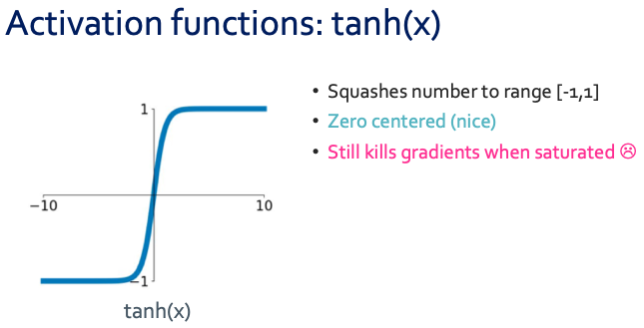
그런데 여전히 첫 번째 문제가 해결이 되지 않았다. 그래서 대안으로 많이 사용되는 함수인 ReLU를 보여주겠다.

◼︎ Overfitting and regularization
NNs는 model이 복잡하다보니 overfittin의 가능성이 굉장히 높다. 그래서 overfitting에서 벗어나기 위해 regularization을 해줘야 한다.
Data augmentation
overfitting을 극복하기 위해 data의 양을 늘리는 방식이다. 그런데 학습 이미지의 개수를 늘리는게 아닌 원본 이미지를 변형하는 방식이다. 반전을 주거나, 대조를 해던가 크롭을 하는등 한 이미지를 여러개로 만드는 방식이다.
Add term to loss
이것은 우리가 배운 regularization 방법과 같은 것이다.
여기에 L1, L2, Elastic을 통해 구현하는 방식이다.
Dropout
이 방식은 서로 연결된 연결망(layer)를 일정 확률로 뉴런을 제거하는 방법이다. 보통 0.5로 hyperparamter를 사용하게 된다. 이렇게 dropout을 사용하면 특정 특성에 과도하게 의존하는 것을 막아 overfitting을 해소시켜준다. 다른 해석법으로는 drop out이 매우 큰 ensemble model이라고 생각하면 된다. 각 이진 노드들이 하나의 modle인것이고 이것들이 다 합쳐진 ensemble model인 것이다. 그래서 overfitting을 해소할 수 있다.
Early stopping
Iteration이 과도하게 많아지면서 overfitting이 일어나기도 한다. 그래서 그냥 일정 iteration부터 training을 멈춰서 overfitting을 피하는 방식도 존재한다.