ML - Lecture 18: Neural Networks part2

앞에서는 neural network가 무엇인지에 대해 배웠다. 이번에는 앞에서 언급한 back propagation을 해볼 것이다.

◼︎ Back propagation

간단한 예시를 통해 back propagation을 해보자.

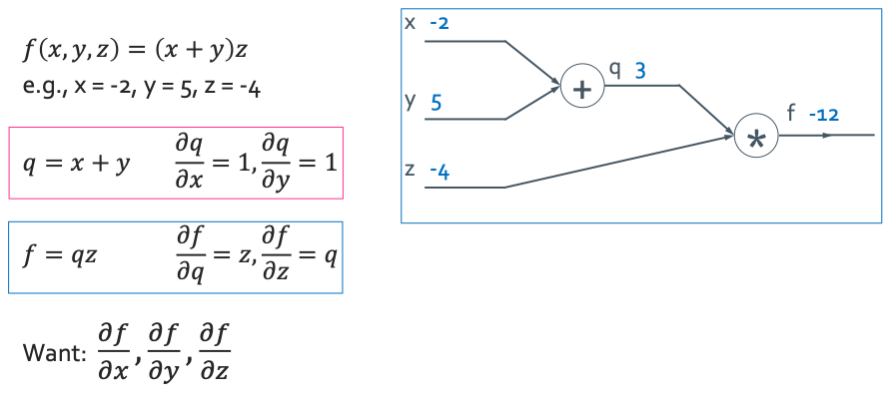
이렇게 $f(x, y, z)$의 함수가 있고 input data가 있었어서 모든 값들과 output값을 구한 것이라고 생각하자. 그리고 변수들에 대해 미분을 해 뒀다. 이제 우리는 $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}$을 구하는 것이 목표이다.

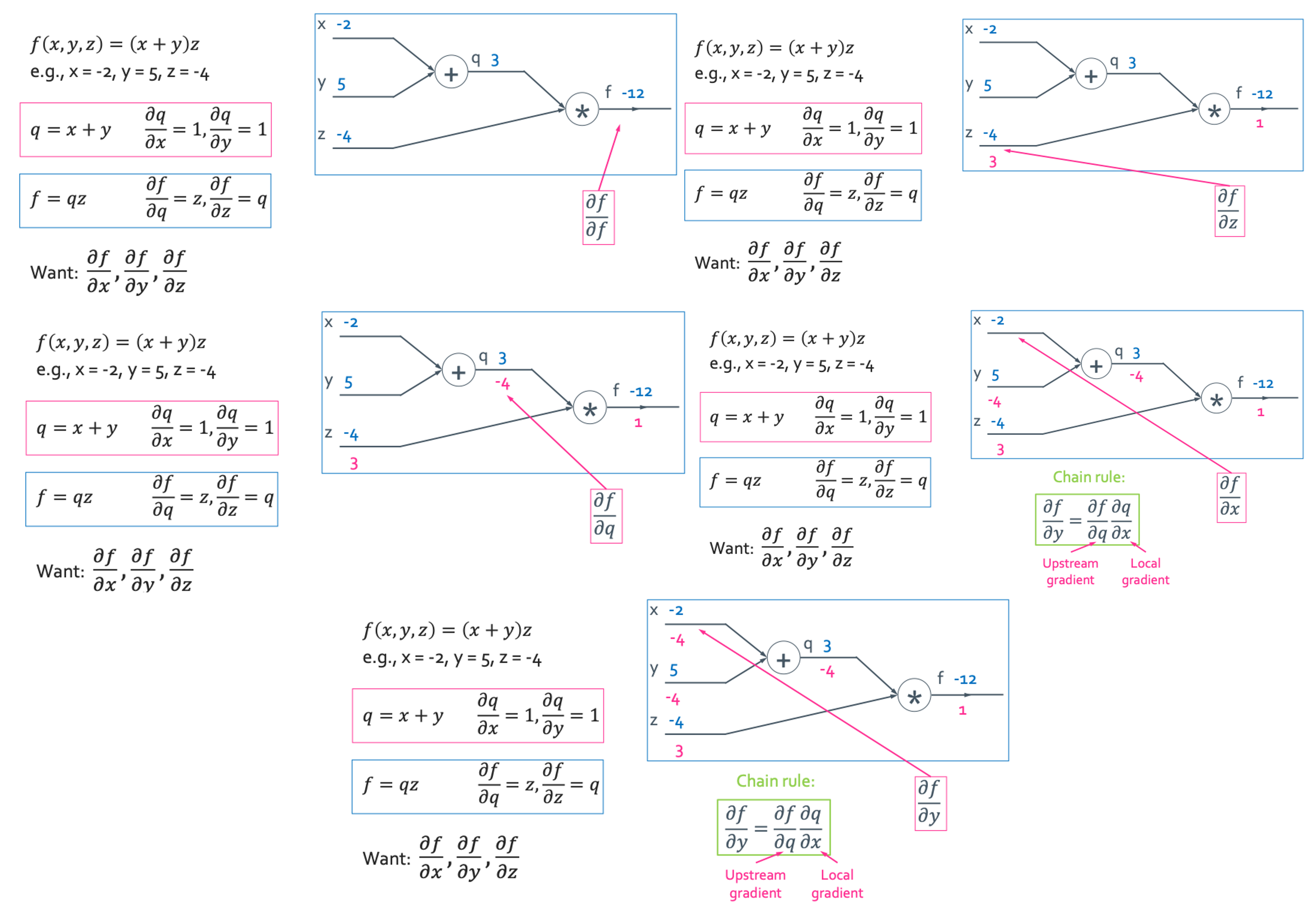
이렇게 뒤에서 시작해서 모든 빈 값을 구해주면 된다. 여기서 알아야하는 용어는 local gradient와 upstream gradient이다. 안 헷깔리는 방법은 안쪽에 있는 gradient은 local하기 때문에 변수들의 관계를 보고 찾아주면 된다.

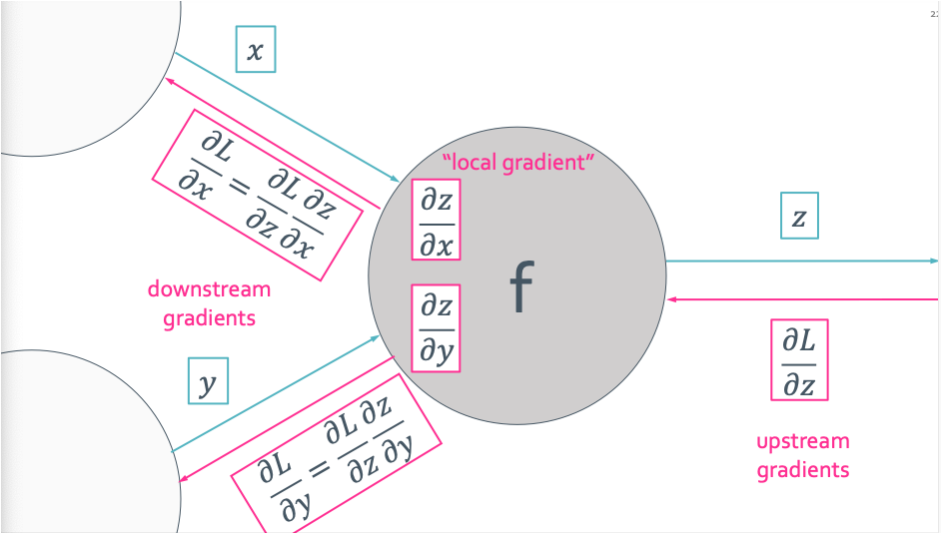
이것을 좀 일반화 하면 다음과 같이 쓸 수 있게 된다.

Back propagation: sigmoid layer

sigmoid layer일 때를 예시로 해서 또 구해보겠다.

Upstream gradient와 local gradient를 이용해서 채워보면 이렇게 된다.

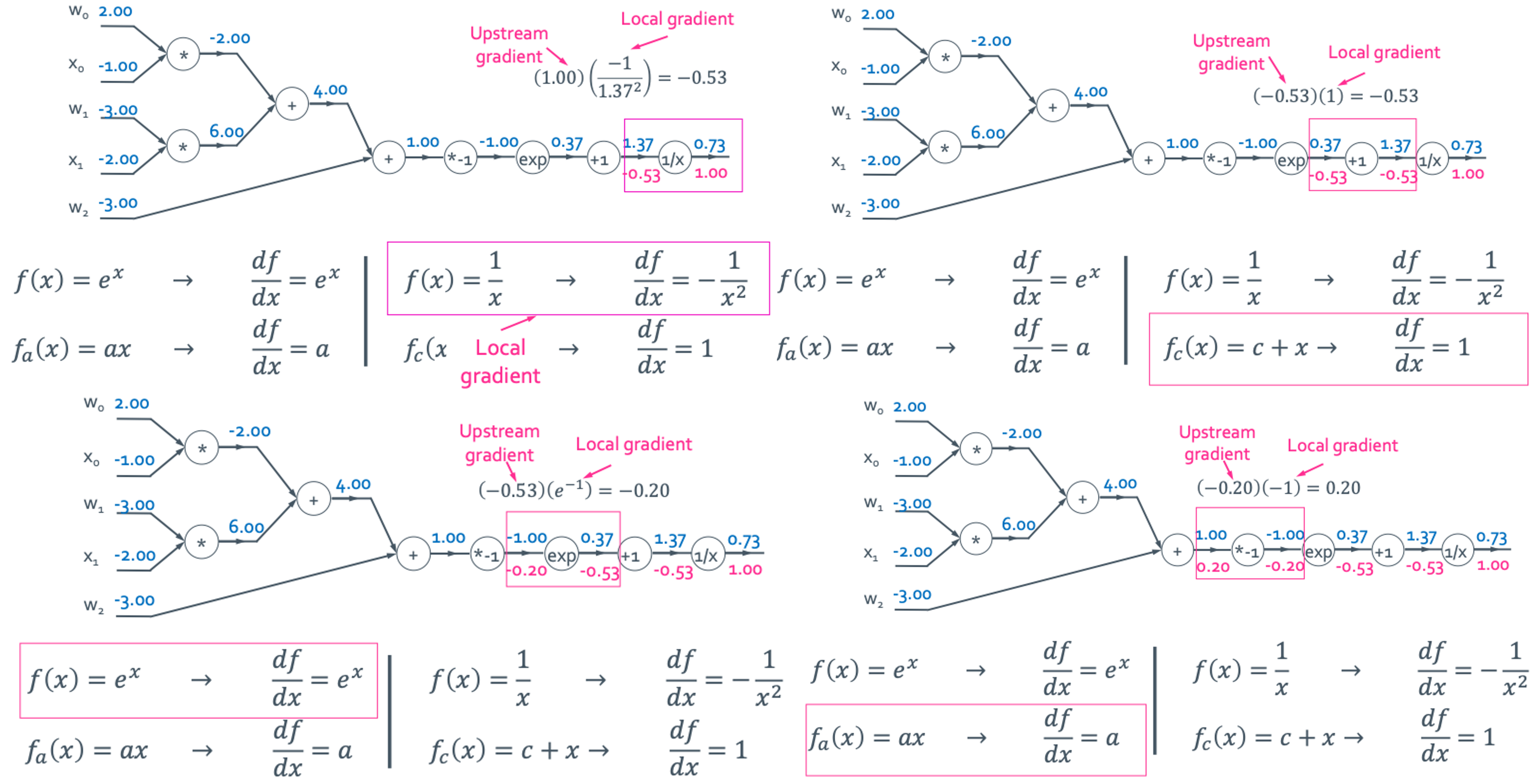
이렇게 하나하나 구했지만 실제로는 중간의 값들까지 구할 필요가 없으면 생략하고 한번에 이런식으로 구해도 된다.

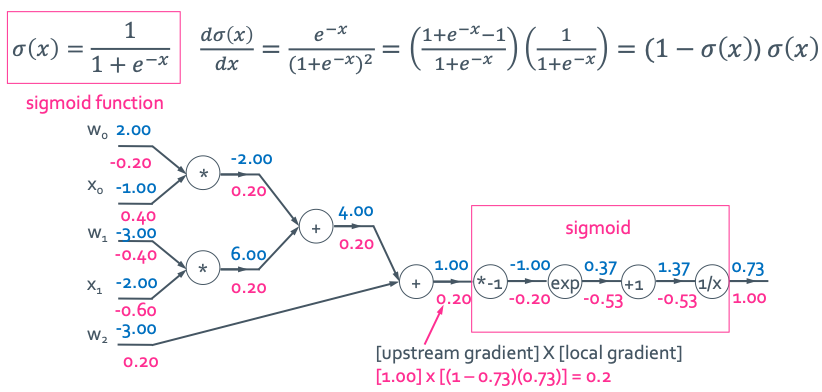
둘이 같은 결과를 가지는 것을 확인할 수 있다.

Pattern in backward flow

계산하다 보면 규칙성을 가지는 곳이 있다는 것을 봤을 것이다. 이것을 정리해서 보여주겠다.

Add gate

Gradient distributor라고 하고 앞과 동일한 gradient값을 나눠주게 된다.

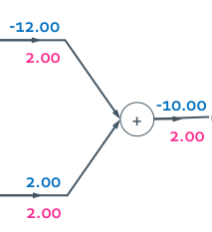
max gate

Gradient router라고 하고 input이 더 큰 곳에 gradient값을 전달하고 작은 곳에는 0을 전달한다.

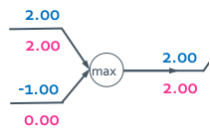
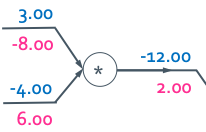
mul gate

Gradient switcher라고 하고 input값과 upstream gradient를 곱하긴 하는데 전달은 반대에 한다.

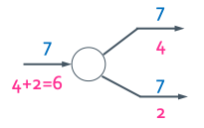
copy gate

Gradient adder라고 하고 gradient들을 더한다.

Vectorization

3가지의 경우의 수가 생길 수 있게 된다.

위에서 다룬 것들은 다 scalar to scalar였다. 이제 vector일때를 추가해서 구해보겠다.

Vector to Scalar

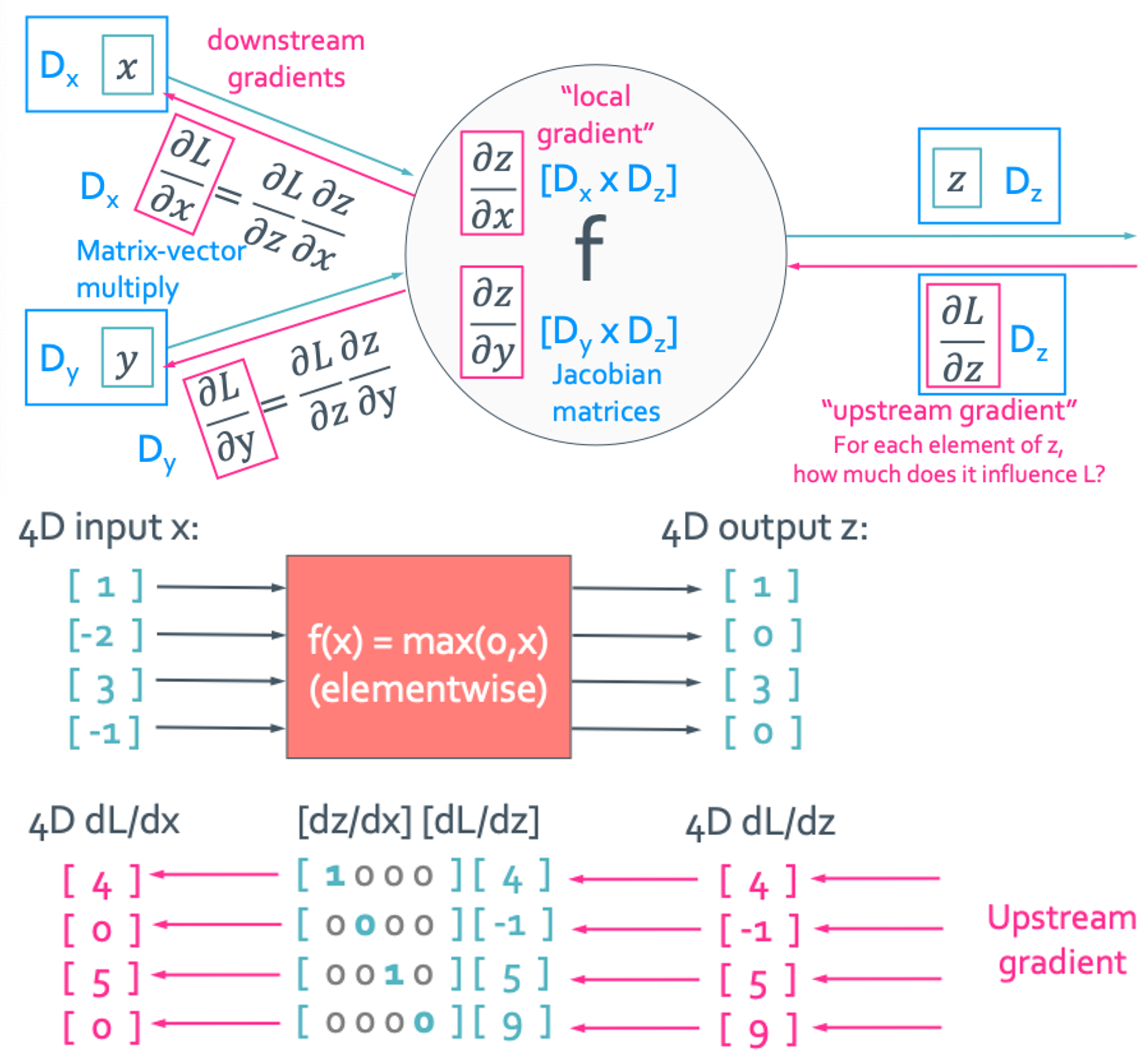
Jacobian 값은 대각 성분 빼고는 무조건 0이니까 다 계산하는게 아니라 inplicit하게 대각성분쪽만 계산하여 연산량을 줄인다.

Vector to Vector

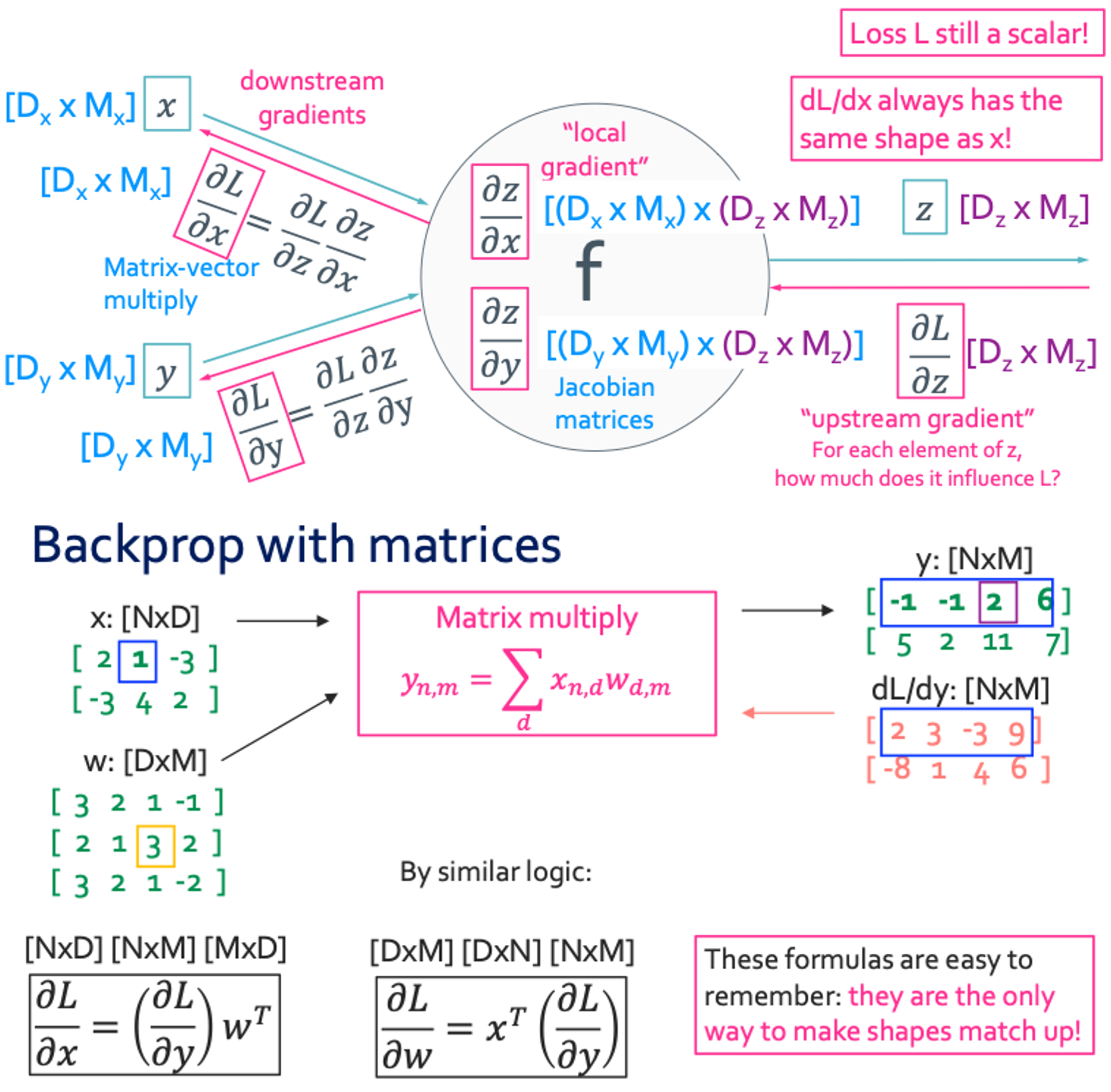
행렬의 갯수를 보고 잘 끼워 맞추면 헷깔리지 않을 것이다.

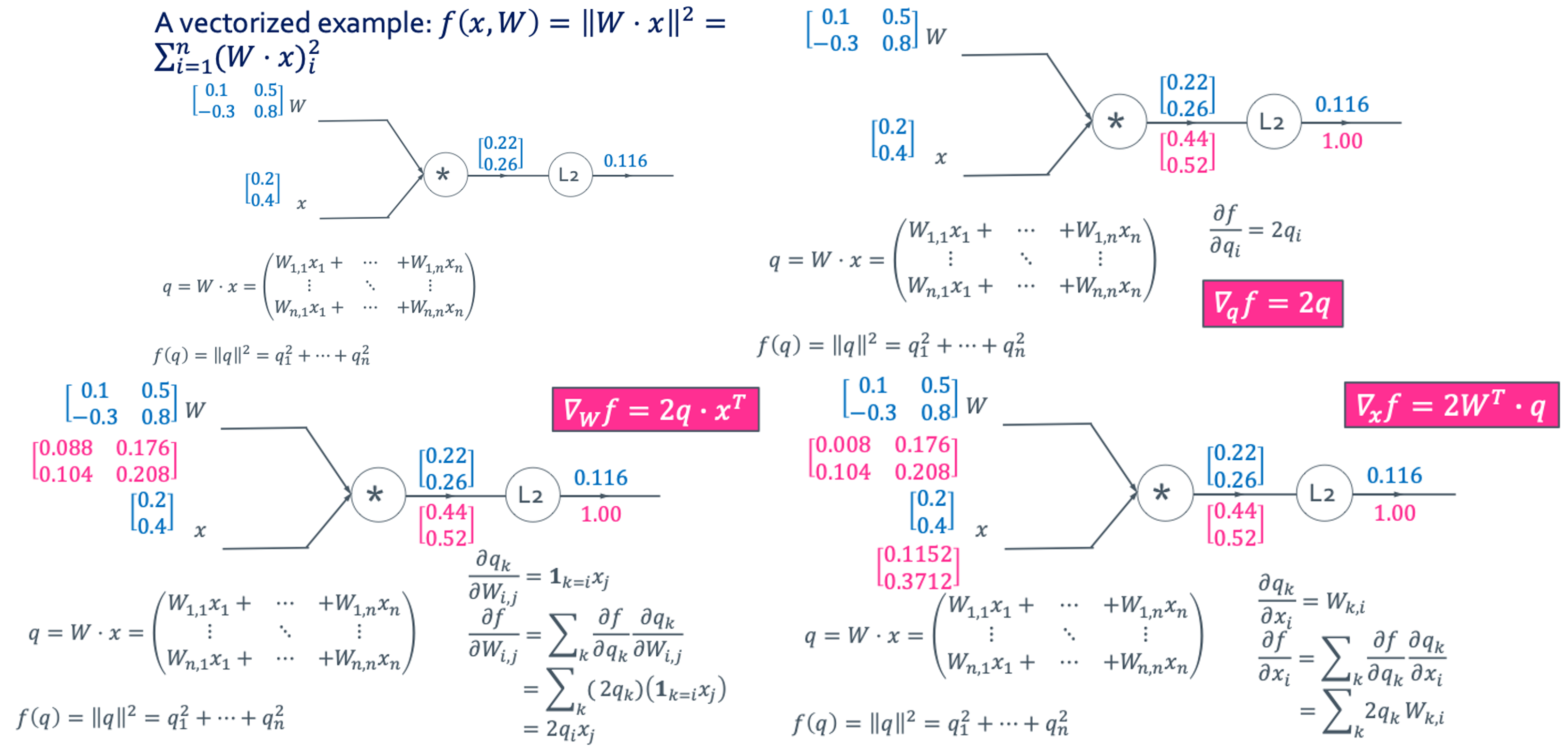
Vectorized example