ML - Lecture 16: Dimension reduction

앞에서 공부를 하면서 느꼈을 것인데 dimension이 크고 그러면 힘들다고 배웠다. 근데 정확히 왜 그런 것일까? 이번 장에서는 그 정확한 이유에 대해 알아보고 PCA와 LDA라는 방법을 통해 dimension을 줄여보는 것을 해 보겠다.

◼︎ The curse of dimensionality

1961년에 Bellman이 새로 만든 단어이다. 이는 dimension이 올라갈 수록(feature의 증가) problem들이 생긴하는 것이다. 예시를 통해 차원의 저주를 체감해보자.

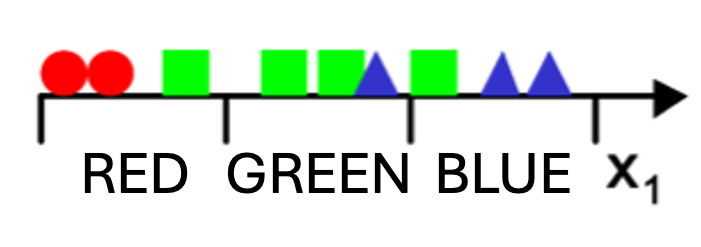
1차원일 때 이렇게 3개의 data bin에 3개의 segment가 들어가있다. 만약 2D로 올리게 된다면 bin은 $3^2=9$개가 될 것이다. 여기에서 2가지 선택할 사항이 있다.

1. density를 유지할 것인가?
   
2. number of examples을 유지할 것인가?

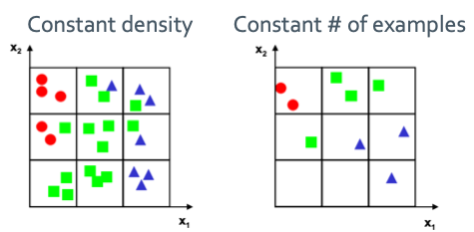
왼쪽은 density를 유지하였고 오른쪽은 example의 개수를 유지하였다. 이번에는 3D로 늘려보겠다.

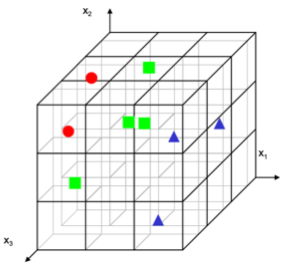
일단 bin의 개수는 $3^3=27$개가 되어야 한다. 그리고 두 가지 선택 사항에 따라 달라지는 것이 있다.

1. Density: 밀도를 유지하고 싶으면 example의 개수가 81개로 늘어나야한다. 이렇게 exponential하게 늘어나야하는 것이다. 그래서 data를 너무나 많이 필요로 하게 된다.
   
2. Number of examples: 이걸 유지하게 되면 위의 사진처럼 텅텅비게 된다. Feature가 늘어나면 data도 같이 늘어나야 learning을 할 수 있는데 너무 부족해서 힘들게 되는 것이다.
   

그러면 이 저주를 어떻게 해결해야할까? Prior knowledge를 이용하기, smoothness를 증가시키는 함수를 제공(regularization), reducing dimensionality가 있다. Regularization은 우리가 해봤고 이번 장에서는 reducing dimensionality이걸 해볼 예정이다. 그냥 data를 있는대로 계속 제공하여 dimension을 늘리면 성능이 좋아질것 같은데 실은 전혀 그렇지 않다.

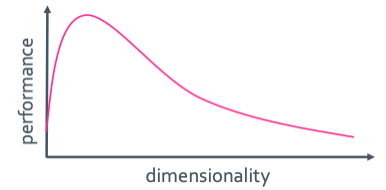
역시 뭐든 과유불급이다.

◼︎ Dimensionality reduction

우선 feature extraction이란 것부터 해보겠다.

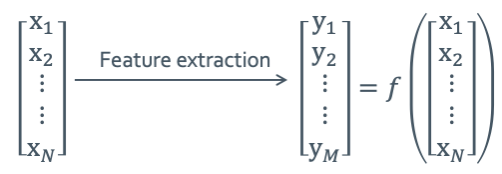
$y = f(x): \mathbb{R}^N \rightarrow \mathbb{R}^M (M < N)$을 만족하는 것부터 찾으려고 한다. 원래는 $f(x)$는 non-linear function이다. 그런데 우선 linear 할 때의 경우부터 해보겠다. 그래서 $y=f(x) \rightarrow y=Wx$로 바꿔서 쓸 수 있다. 그러면 아래의 그림처럼 matrix의 형태로 만들어줄 수 있다.

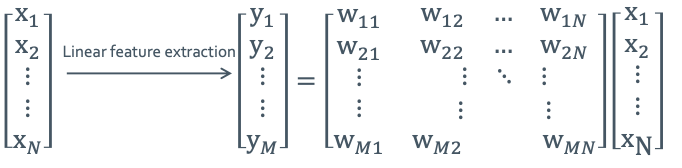
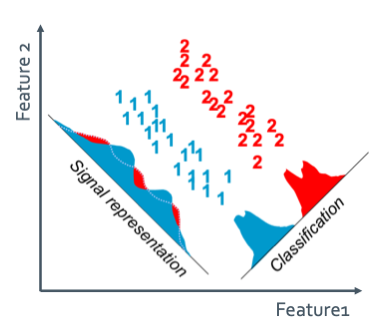
이렇게 extraction을 할 때 objective function을 maximize하거나 minimize하는 것을 찾아야하는데 2가지의 criteria가 있다.

1. Signal representation
   
   • Lower-dimension space를 하여 sample의 accuracy를 본다.(분산을 본다)
     
   • 이 방법이 PCA(Principal Components Analysis)이다.
   • Unsupervised
2. Classification
   
   • Lower-dimension space를 하여 class-discriminatory한 information으로 나오게 한다.(특징 별로 분류한다.)
     
   • 이 방법이 LDA(Linear Discriminant Analysis)이다.
   • Supervised

◼︎ PCA

PCA는 데이터를 축에 사영했을 때 가장 높은 분산을 가지는 데이터의 축을 찾아 그 축으로 차원을 축소하는 방법을 말한다. 그렇게 찾은 축을 주성분이라고 한다. 일단 정사영을 하기 위해 그람 행렬을 이용해볼 것이다.

$\mathbf{G} = w_i^Tw_j \; (w_i \text{is orthonormal basis vector})$

그람 행렬을 구했으면 그 space에 projected된 vector $\hat{x_d}$도 필요하다.

$\hat{x_d} = w_i^Tx_d$

나중에 variance를 구하기 위해 mean값을 구할 것이다. 그런데 정사영된 mean값도 알아야 한다. 그래서 mean of the vectors in the original space는 $\bar{x}$이고 mean of samples in the projected space는 $x$이다. 그리고 다음과 같은 관계를 가진다.

$x = w_i^T\bar{x}$

그래서 variance를 구하면 다음과 같다.

$\begin{align} \sigma^2(\hat{x}) = \frac{1}{D} \sum_{d=1}^{D} (\hat{x_d} - x)^2 = \frac{1}{D} \sum_{d=1}^{D} (w_i^Tx_d - w_i^T\bar{x})^2 \newline = \frac{1}{D} \sum_{d=1}^{D} (w_i^Tx_d - w_i^T\bar{x})(w_i^Tx_d - w_i^T\bar{x})^T \newline = \frac{1}{D} \sum_{d=1}^{D} w_i^T(x_d - \bar{x})(x_d - \bar{x})^T w_i \newline = w_i^T (\sum \mathbf{x}) w_i \end{align}$

Covariance matrix of x: $\sum \mathbf{x} = \sum_{d=1}^{D} (x_d - \bar{x})(x_d - \bar{x})^T$

최종적으로 objective function은 다음과 같이 Lagrange muliplier를 이용하여 나타낼 수 있다.

$J(w_i) = w_i^T (\sum \mathbf{x}) w_i + \lambda_i (1 - w_i^T w_j)$

이제 항상하던 미분해서 0되는 값 찾으면 된다.

$\begin{align} \frac{\partial}{\partial w_i} J(w_i) = \frac{\partial}{\partial w_i} [w_i^T (\sum \mathbf{x}) w_i + \lambda_i (1 - w_i^T w_j)] \newline = 2(\sum \mathbf{x} w_i - \lambda_i w_i ) = 0 \newline \Rightarrow \sum \mathbf{x} w_i = \lambda_i w_i \end{align}$

그러면 행렬 $\sum \mathbf{x}$에 대해 $w_i$는 eigenvectors, $\lambda_i$는 eigenvlues이다.

그러면 최종적으로 variance를 구할 수 있게 된다.

$\begin{align} \sum \mathbf{x} w_i = \lambda_i w_i \newline \sum w_i^T \mathbf{x} w_i = w_i^T \lambda_i w_i \newline \therefore \sum w_i^T \mathbf{x} w_i = \lambda_i = \sigma^2(\hat{x}) \end{align}$

앞에서 PCA는 가장 큰 분산일때를 구하는 것이라고 했다. 그렇기 때문에 가장 큰 고윳값을 선택하게 되고 그때의 고유벡터를 $w_i$로 구하면 된다. 2차원일 때를 가정하여 시각화하면 다음과 같다.

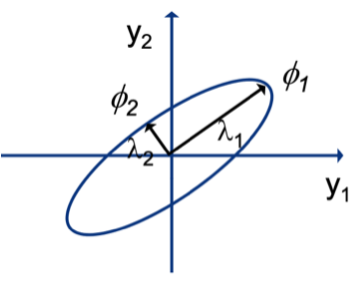
이제 좌표 위에 있던 data값들을 $\phi_1$축으로 다 정사영시키면 되는 것이다.

◼︎ LDA

축을 잘 설정해서 모든 data를 정사영 시켰을때 classified된 값들이 서로 잘 뭉쳐있게 만드는 축을 찾을 수 있을 것이다. 이런 축을 구하는 것이 LDA이다.

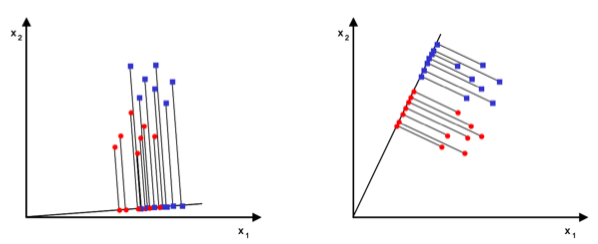
$y = w^Tx$의 정사영된 scalar $y$를 이용할 것이다. 앞에서 classificaion할 때 처럼 center값인 $\mu_i$값을 구할 것이다.

$\mu_i = \frac{1}{N_i} \sum_{x \in w_i} x$, $\tilde{\mu_i} = \frac{1}{N_i} \sum_{y \in w_i} y = \frac{1}{N_i} \sum_{x \in w_i} w^Tx = w^T \mu_i$

이를 이용하여 objective function을 구하면 다음과 같다.

$J(w) =|\tilde{\mu_1} - \tilde{\mu_2}| = |w^T(\mu_1 - \mu_2)|$

이렇게 구한 objective function이 과연 맞는 방식일까? 일단 objective function의 값이 클때, 즉 평균끼리 서로 차이가 많이 날 때 좋다는 결론을 낼 수 있을 것이다.

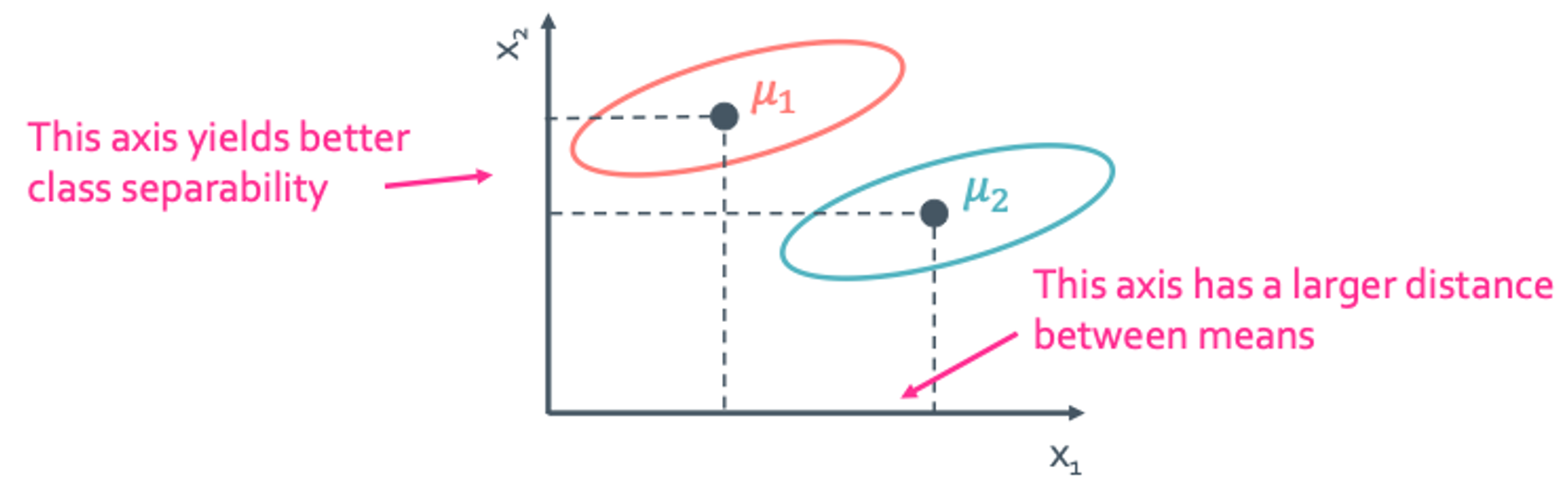
이 예시를 보면 $x_1$으로 내릴때 오히려 $x_2$로 내릴때에 비해 classification이 뚜렷하지 않을 것을 확인 할 수 있다. 그러면 이 objective function은 잘못 되었다는 것을 알 수 있다.

Fisher’s solution

그래서 나온 해결법이 Fisher’s solution이다. 그는 평균의 차이만 큰것을 구하면 안되고 다른 요소가 더 들어가있어야한다고 했다. 그것이 바로 within-class scatter를 고려한 식이다. 이 within-class scatter는 variance와 같다. 일단 classification을 사용할 때는 variance가 작은게 좋다. 그래서 구한 scatter는 다음과 같다.

$\tilde{s_i}^2 = \sum_{y \in w_i} (y - \tilde{\mu_i})^2$, within-class scatter = ($\tilde{s_1}^2 + \tilde{s_2}^2$)

이를 이용해 fisher’s solution은 다음과 같다.

$J(w) =\frac{|\tilde{\mu_1} - \tilde{\mu_2}|^2}{\tilde{s_1}^2 + \tilde{s_2}^2}$

그런데 이 상태로 있으면 우리가 사용을 하지 못한다. 우리가 계산할 수 있는 식으로 바꿀 것이다. 일단 다음과 같이 초기 조건을 변형 시켜보자.

$S_i = \sum_{y \in w_i} (y - \tilde{\mu_i})(y - \tilde{\mu_i})^T$, within-class scatter = $S_1 + S_2 = S_W$

자 이제 계산을 해보자.

$\begin{align} \tilde{s_i}^2 = \sum_{y \in w_i} (y - \tilde{\mu_i})^2 = \sum_{x \in w_i} (w^Tx - w^T \mu_i)(w^Tx - w^T \mu_i)^T \newline = \sum_{x \in w_i} w^T(x - \mu_i)(x - \mu_i)^T w \newline = w^T S_i w \newline \therefore \tilde{s_1}^2 + \tilde{s_2}^2 = w^T (S_1 +S_2) w =w^T S_W w \end{align}$

분모 부분은 해결했으니까 이제 분자 부분을 해결해줘야 한다,

$(\tilde{\mu_1} - \tilde{\mu_2})^2 = (w^T \mu_1 - w^T \mu2)^2 = w^T (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T w = w^T S_B w$

• $S_B$: between-class scatter matrix라고 하자

그러면 최종적으로 objective function은 다음과 같이 쓸 수 있다. 이것을 Rayleigh quotient라고 한다.

$J(w) =\frac{|\tilde{\mu_1} - \tilde{\mu_2}|^2}{\tilde{s_1}^2 + \tilde{s_2}^2} = \frac{w^T S_B w}{w^T S_W w}$

보통은 이렇게 되어있어도 유리함수 형태이다보니 이용하기가 어렵다. 하지만 이걸 쉽게 이용하는 방법이 있다.

$max w^T S_B w$ subject to $w^T S_W w = K$
로 만들어버리면 된다. 어떻게 하는거냐면 $w^T S_W w$를 $K$라는 contraint로 가정하여 이 K에 대한 $max w^T S_B w$를 구하는 것이다. 그러면 Lagrange multipliers를 사용할 수 있게 된다.

$L(W) = w^T S_B w - \lambda (w^T S_W w - K)$

이것을 $\nabla_w L(w) = 2(S_B - \lambda S_W)w = 0$을 이용하면 결론은 다음과 같이 나온다.

$S_B w = \lambda S_W w $

일단 LDA에는 대전제가 하나가 있다. 무조건 distribution은 gaussian을 따라야한다는 것이다.