ML - Lecture 15: Clustering
일단 clustering(군집화)이 뭘까? Clustering은 유사성이나 같은 패턴을 가지는 객체들을 그룹으로 묶는 것이라고 생각하면 된다. 앞에서 배운 classification이나 그런 분류와 뭐가 다르냐는 생각일 들 것이다. 크게 차이나는 부분은 clustering은 unsupervised learning이라는 것이다. 언제까지 인간이 모든것을 분류하고 있을수 없다. 이 분류조차도 혼자서 unspervised하게 찾을 수 있게 할 필요성이 있었다. 그래서 clustering이라는 개념이 나온 것이다.
◼︎ Clustering: An unsuperviesd learning task
원래 분류를 할때는 label에 따라서 카테고리별로 분류를 하게 된다. 그런데 앞에서 말했듯 이건 unsupervised learning이다. 그래서 label이 제공되지 않고 input data만 있다. 그래서 이 data들로 cluster는 center와 shape/spread라는 것을 찾게된다. 그렇게 적용하면 다음과 같은 사진처럼 대충 clustering된다고 생각하면 된다.
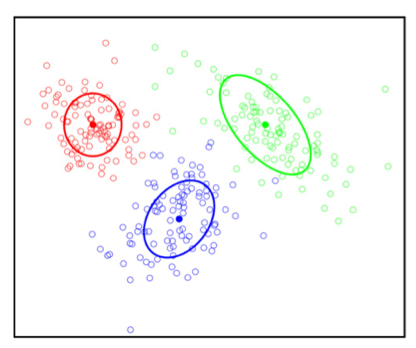
그런데 이렇게 딱딱 이쁘게 구분되어 있는게 아니다. 심지어 지금 보면 shape는 타원형태를 띄고 있는데 정말 다양한 모양이 가능하다.
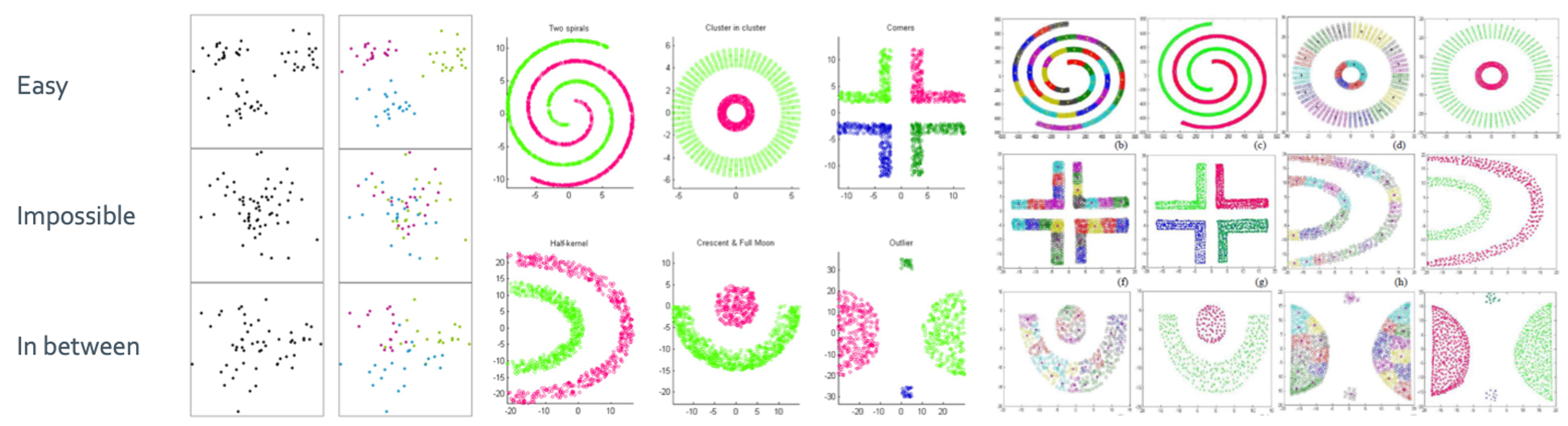
◼︎ k-means: A clustering algorithm
k-means라는 방법을 이용할 것이다. 일단 $\text{Score} = \text{distance to cluster center}$라는 요소를 추가할 것이다. 이 score는 작을수록 좋은 것이다. 알고리즘의 순서는 다음과 같다.
- 임의의 K값을 정하여 K개의 cluster centers를 initialize 한다. ($\mu_1, \mu_2, …, \mu_k$)
- 각 data와 center와의 거리를 계산하고 가장 가까운 중심을 선택한다.
$z_i \leftarrow \operatorname{argmin}_j \Vert \mu_j - x_i \Vert_2^2$
- 위의 결과에 따라 center를 다시 update한다.
$\mu_j = (1/n_j) \sum_{i:z_i=j} x_i$
- converge할 때 까지 2, 3 단계를 반복한다.
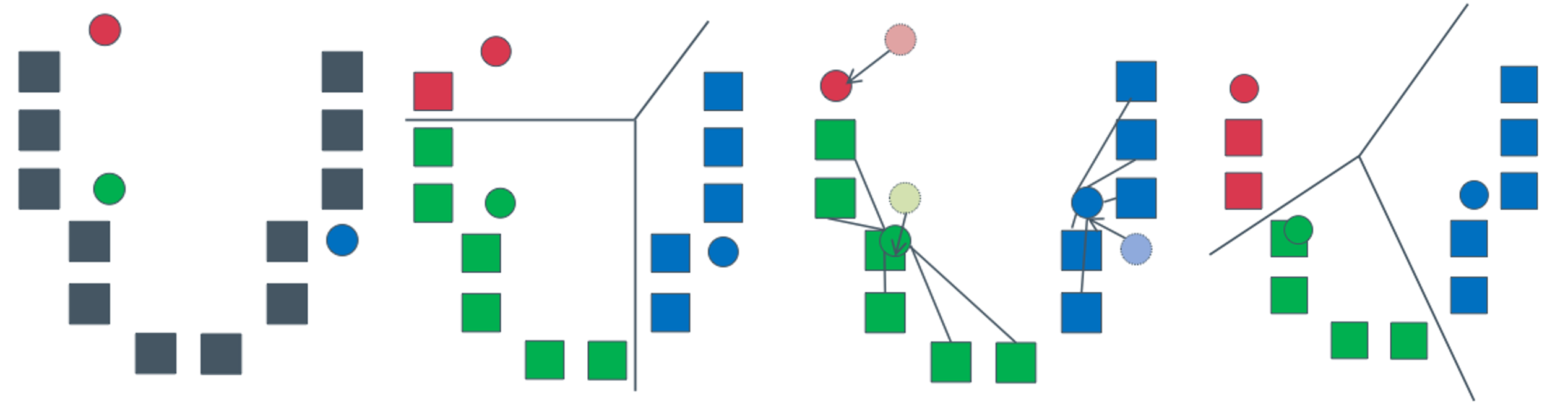
k-means as coordinated descent
1.
$z_i \leftarrow \operatorname{argmin}_j \Vert \mu_j - x_i \Vert_2^2$
2.
$\mu_j = (1/n_j) \sum_{i:z_i=j} x_i = min_{\mu} \sum_{i:z_i=j} \Vert \mu_j - x_i \Vert_2^2$
위에서 이렇게 2개의 계산 식을 구하였다. 이제 이 2개의 식을 이요하여 coordinate descent를 할 것이다.
Coordinate descent = Alternating minimization 1.($z$ given $\mu$) and 2.($\mu$ given $z$) = 1.과 2.를 번갈아가며 반복하는 과정
k-means는 local optimum으로 converge하게 된다. 그렇기 때문에 initialize(처음에 center를 어디에 설정하는지)에 따라 결과가 달라지게 된다.
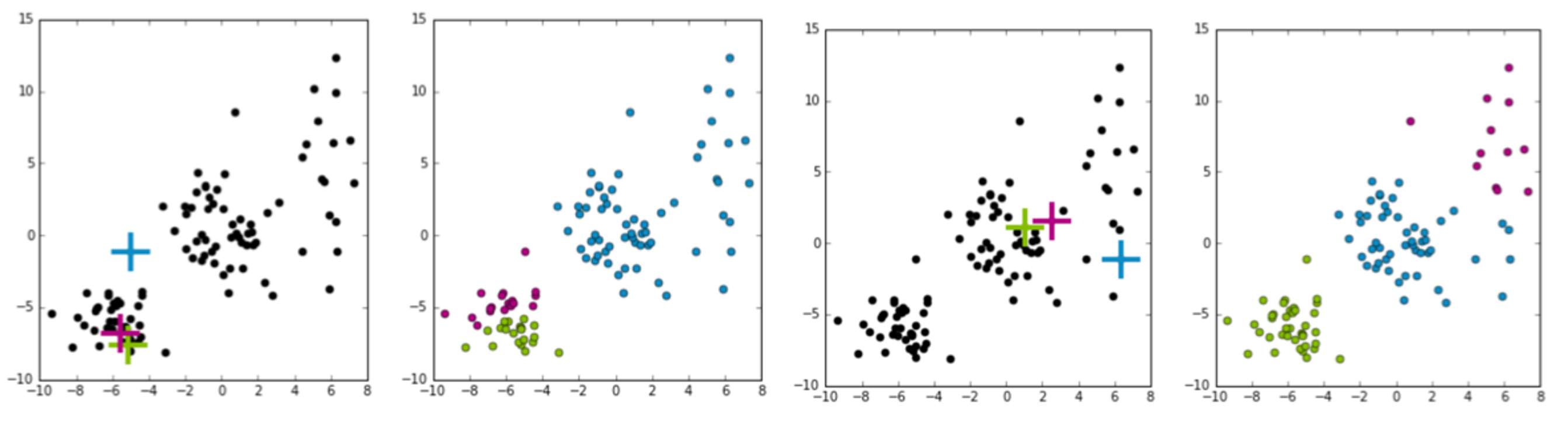
실제로 이렇게 왼쪽과 오른쪽이 아르게 나오게 된다. 그런데 둘 중 어니게 더 좋은것 같은가? 당연 두 번째가 더 분류가 잘 나눠졌다고 볼 수 있다. 그런데 우리는 이걸 직관적으로 판단했는데 이 machine은 어떻게 이걸 판단할 수 있을까? 이게 바로 앞에서 정의했던 score를 사용할 때가 됐다는 것이다. 그래서 최종적으로 구한 k-means의 공식은 다음과 같다.
$\sum_{j=1}^{k} \sum_{i:z_i=j} \Vert \mu_j - x_i \Vert_2^2$
이게 작을수록 좋다. 그런데 여기서 k가 점점 커지면 어떻게 될까? data가 너무 세분화되다 보니까 overfitting이 일어나게 된다. 게다가 만약 k=N이라는 extreme한 상황까지 가면 모든 center가 data에 일치하게 되어 heterogeneity=0이라는 결과가 나오게 된다.