ML - Lecture 14: Instance-Based Learning
이번 장에서는 Nearest neighbor, kernel regression, 그리고 이를 이용하는 classification에 대해 다룰 것이다. 지금까지 우리는 선형적이고 항수가 하나로 나타나는 그러한 것들만 봤다.
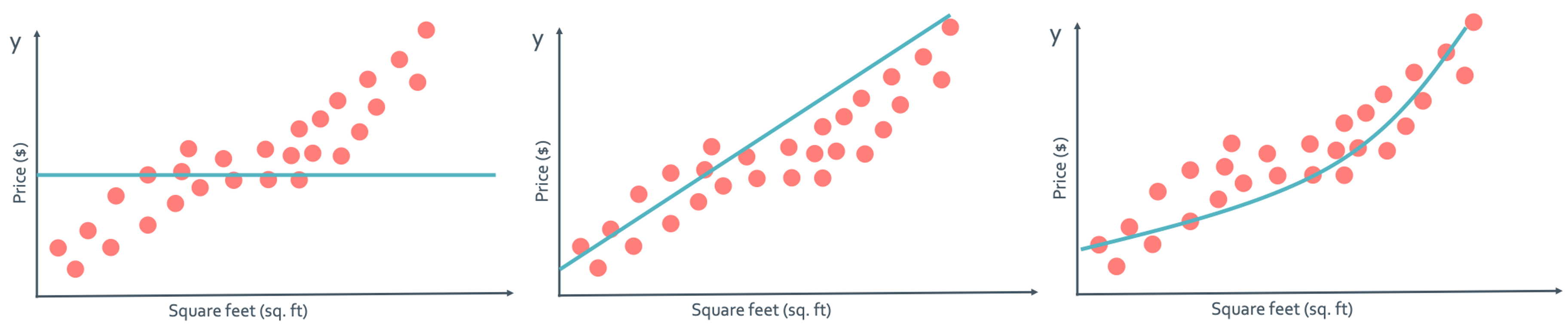
이렇게 polynomial한 경우만 봤는데 이런걸 globally fit이라고 한다. 하지만 실제로는 그렇지 않은 경우가 더 많다. locally fit하게 $f(x)$를 만들어야 할 때가 더 많을 것이다. 아래의 그래프가 그러한 상황이다.
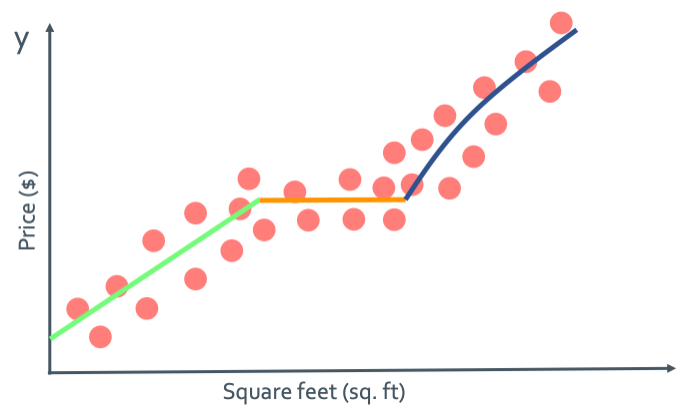
이런 local structure로 된 $f(X)$를 만들기 위해서는 어떻게 해야할까?
◼︎ Nearest neighbor regression
이 방법은 가장 similar한 값을 찾는 방법이다. 그래서 구간을 나누고 locally하게 비슷한 값을 찾는 것이다. 장점으로는 training process에 시간을 많이 쓰지 않는다는 것이지만 단점으로는 test에 시간을 많이 사용하게 된다는 것이다.
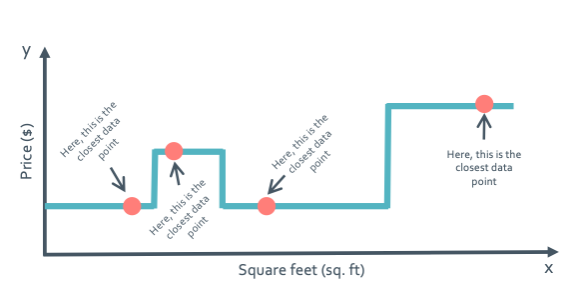
이것은 1 nearest neighbor(1-NN) regression을 진행한 것이다. 어떤 dataset이 $(x_N, y_N)$의 형태를 가지고 있을 때 $x_q$에서의 nearest neighbor를 찾는다고 하면 다음과 같은 식을 이용하면 된다.
$\hat{x_i} = \operatorname{argmin} \, \operatorname{dist}(x_q, x_i) (\text{where} \, i\in{1, 2, ..., N})$
그래서 $y_q = \hat{y_i}$이다.
이렇게 구한 algorithm으로 dimension을 늘리면 다음과 같은 결과를 얻을 수 있다.
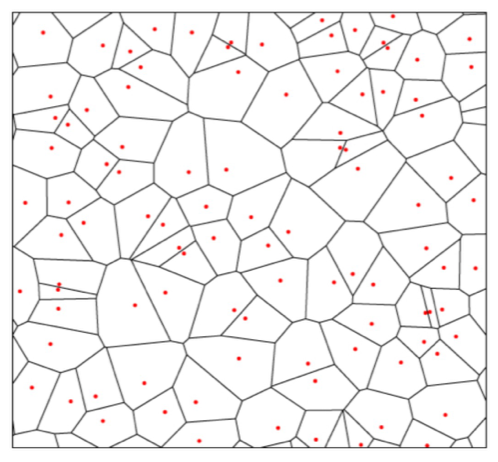
Distance metrics
앞에서 만든 algorithm을 보면 dist 함수가 있다. 그런데 이 가깝다란 의미와 distance를 어떻게 정의를 해야할까? 우선 1차원에서는 euclidean distance($\operatorname{Distance}(x_j, x_q) = |x_j - x_q|$)를 사용한다. 그런데 다차원에서는 정의가 달라져야 하게 된다. Euclidean 방식의 높은차원에 대한 거리의 정의는 다음과 같다.
$\operatorname{Distance}(x_j, x_q) = \sqrt{a_1(x_j[1]-x_q[1])^2 + ... + a_d(x_j[d]-x_q[d])^2 }$
Other example distance metrics: Mahalanobis, rank-based, correlation-base, cosine similarity, Manhattan, Hamming, … 어떤 metric을 사용했냐에 따라 그림이 되게 다르게 나온다. 그러면 이렇게 나눠진 1-NN을 classification으로 만들 수 있다.
◼︎ 1-NN algorithm
’’’ initialize Dist2NN = inf, x = [] for i = 1, 2, …,N delta = distance(x_i, x_q) if delta < Dist2NN set x = x_i set Dist2NN = delta
return most similar x_i ‘’’ 이 알고리즘은 data가 얼마나 잘 고르게 분포되어 있냐에 따라 좋은지 안좋은지를 알 수 있다.
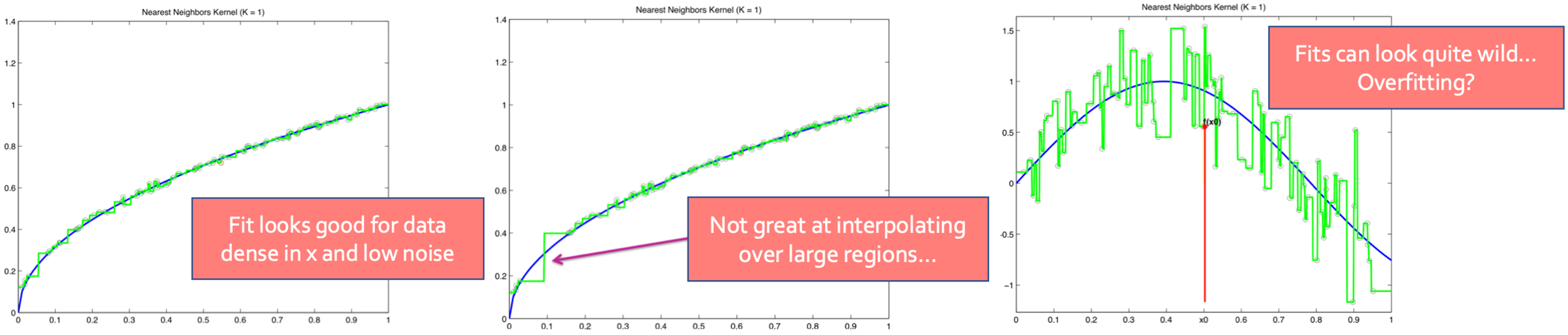
오른쪽으로 갈 수록 data가 고르게 있지 않아 sample이 없어 오차가 굉장히 커지게 되는 것을 볼 수 있다.
◼︎ K-nearest neighbors
1-NN에서는 하나의 $x_q$를 찾을 때 하나의 $x_i$의 값과 대조하여 구하게 된다. 하지만 이는 주변에 data가 없으면 거리가 커져 좋지 않은 model이 된다. 그래서 k-NN은 이것을 보안하였다. 하나의 $x_i$만이 아닌 주변의 k개의 neighbor를 고려하는 것이다.
$(x_{NN_1}, x_{NN_2}, ..., x_{NN_k}) → (y_{NN_1}, y_{NN_2}, ..., y_{NN_k}) $
그래서 $y_q = \frac{1}{N} \sum_{i=1}^{k}y_{NN_i}$이다.
하지만 이 방법도 완벽한 것은 아니다.
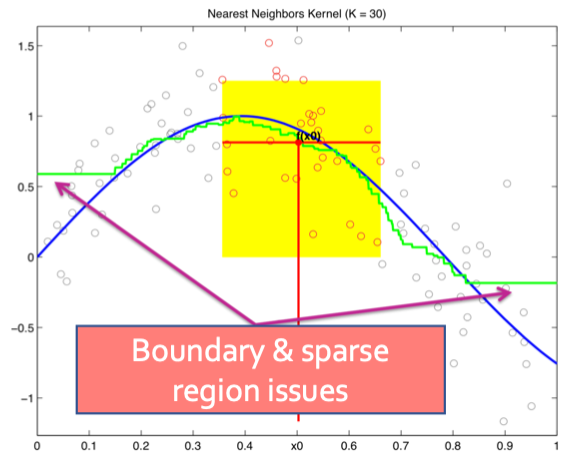
중간 쪽을 보면 확실히 noise가 줄어든 것을 볼 수 있다. 하지만 얖 끝점을 보면 오히려 안좋게 된 것을 볼 수 있다.
◼︎ Weighted K-nearest neighbors
그래서 여기에 wight를 도입하는 것이다.
$\hat{y_q} = \frac{C_{qNN_1}y_{NN_1}+C_{NN_1}y_{qNN_1}+C_{NN_1}y_{NN_1}+...+ C_{qNN_1}y_{NN_1}}{\sum_{j=1}^{k} C_{qNN_j}} $
과연 weight인 $C_{qNN_j}$를 어떻게 정의해야할까?
$C_{qNN_j} = \text{Kernel}_{\lambda}(|x_{NNj}-x_q|)$
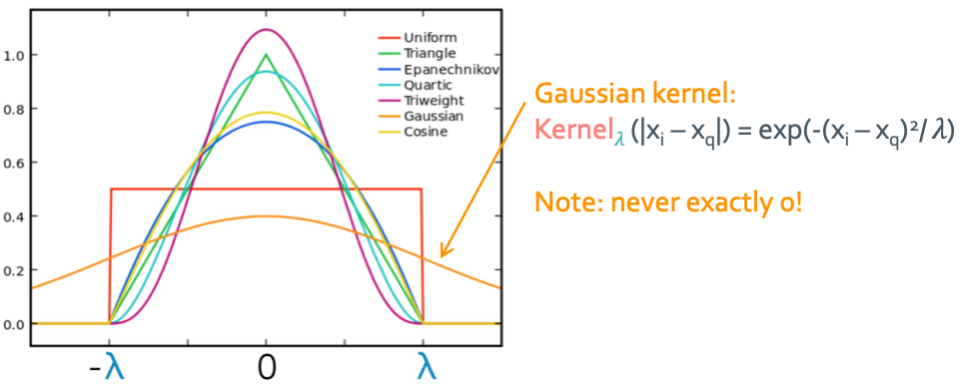
이렇게 어떤 kernel(밀도의 역할)을 선택하냐에 따라 model이 달라지게 된다.
Kernel regression
위에서 구한 weight를 이용해 regression을 해볼 것이다.
$\hat{y_q} = \frac{\sum_{i=1}^{N} C_{qi}y_i}{\sum_{i=1}^{N} C_{qi}} = \frac{\sum_{i=1}^{N} \text{Kernel}_{\lambda}(\operatorname{dist}(x_i,x_q))*y_i}{\sum_{i=1}^{N} \text{Kernel}_{\lambda}(\operatorname{dist}(x_i,x_q))}$
그래서 bandwidth를 뜻하는 $\lambda$에 의해 model의 정확도가 달라지게 된다.
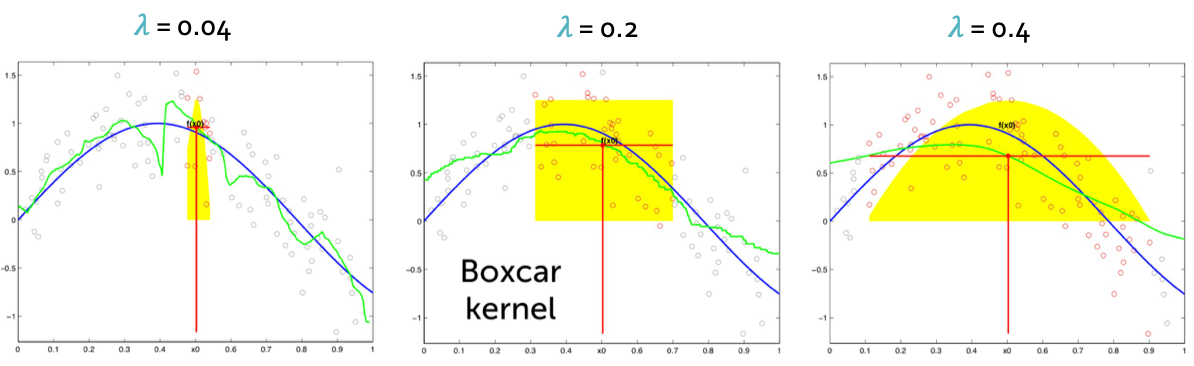
위의 공식을 자세히 보면 global이나 local이나 식의 형태는 비슷한 것을 알 수 있다. 다른 점은 global은 C가 항상 같은 constant값을 가지는 것이고 local은 C가 weight로서 i에 따라 다른 값을 가지게 되는 것이다.