ML - Lecture 13: Evaluating classifiers: Precision & Recall

지금까지 우리는 classifier에 대하여 배우면서 어떤 얼마나 좋은지 나쁜지 이런거에 대해 분류를 했었다. 그런데 과연 이 classifier가 정확한지 안한지는 어떻게 알 수 있을까? 정확하기만 한 classifier는 항상 믿을 수 있는 것일까? 이러한 이유로 다양한 evaluation을 도입하였다. 일단 크게 두 가지를 나눠서 볼것이다. 초점을 맞추는 점으로는 내가 negative인 것을 positive라고 잘못된 분류를 했는지(precision), 그리고 내가 positive한것을 다 분류하지 못했는지(recall)에 대하여 이다.

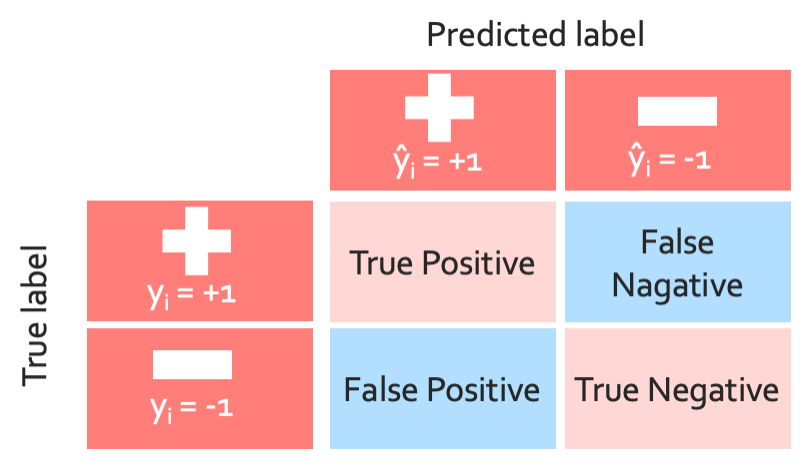
◼︎ Precision

Fractrion of positive predictions that are actually positive이다. Accuracy, precision, recall의 위의 표에서 미리 생각해보자면 accuracy대각성분을 뜻하고 precision은 1열, recall은 1행이다. 이것을 공식으로 나타내면 다음과 같다.

$\operatorname{Precision} = \frac{\text{# true positives}}{\text{# true positives}+\text{# false positive}}$

◼︎ Recall

Fractrion of positive data predicted to be positive이다.

$\operatorname{Recall} = \frac{\text{# true positives}}{\text{# true positives}+\text{# false negatives}}$

◼︎ Precision - Recall extremes

• Optimistic model(거의 positive하게 평가함): Low precision, High recall
• Pessimistic model(거의 negative 평가함): High precision, Low recall

◼︎ Tradeoff Precision and Recall

Precision과 Recall은 서로 tradeoff의 관계에 있다. 그래서 이를 잘 balance있게 사용하는 것이 중요하다. 그래서 classifier를 다음과 같이 설계할 수 있다.

P(y|X) = estimate of class probabilities

if(P(y=+1|X)) > 0.5: //여기를 숫자를 바꾸면 optimistic한지 passimistic한지 조절할 수 있다.
    y_i = +1
Else:
    y_i = -1

그래서 passimistic한 classifier는 이렇게 만들면 된다.

P(y|X) = estimate of class probabilities

if(P(y=+1|X)) > 0.999: //여기를 숫자를 바꾸면 optimistic한지 passimistic한지 조절할 수 있다.
    y_i = +1
Else:
    y_i = -1

Optimistic한 경우는 이렇다.ㄴ

P(y|X) = estimate of class probabilities

if(P(y=+1|X)) > 0.001: //여기를 숫자를 바꾸면 optimistic한지 passimistic한지 조절할 수 있다.
    y_i = +1
Else:
    y_i = -1

이렇게 threshold를 설정하여 optimistic한지 pessimistic한지 결정할 수 있다.

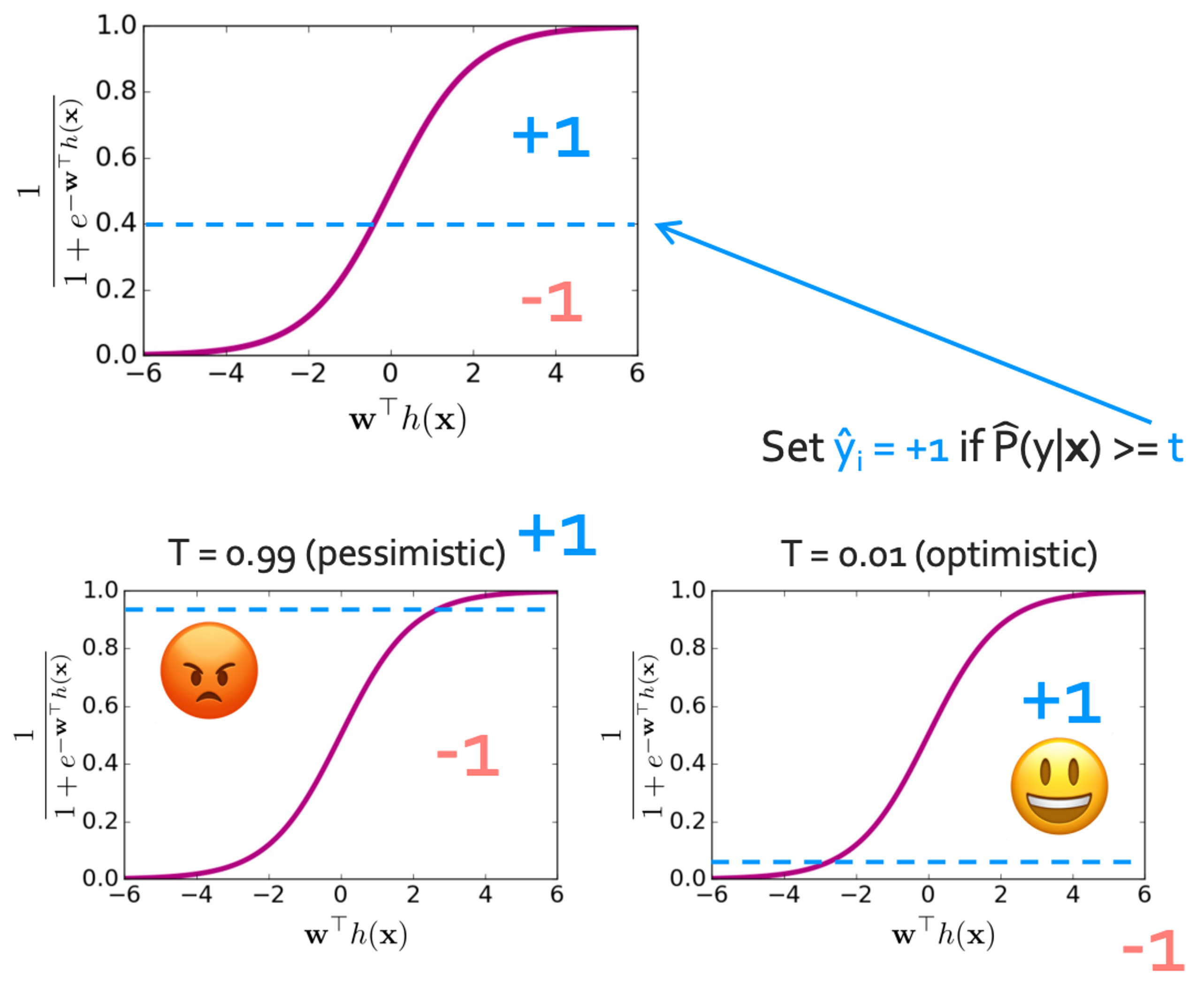
◼︎ Precision - recall curve

이 두개를 한눈에 보는 방법이 있는데 바로 precision recall curve를 이용하는 것이다.

보통의 classifier는 주황색처럼 꺾이는 곡선만 만들어질 텐데 이상적인 classifier는 상수 함수같은 파란색 곡선이다. 이를 보면 위로 많이 올라가 있을수록 좋은 classifier라는 것을 알 수 있다.

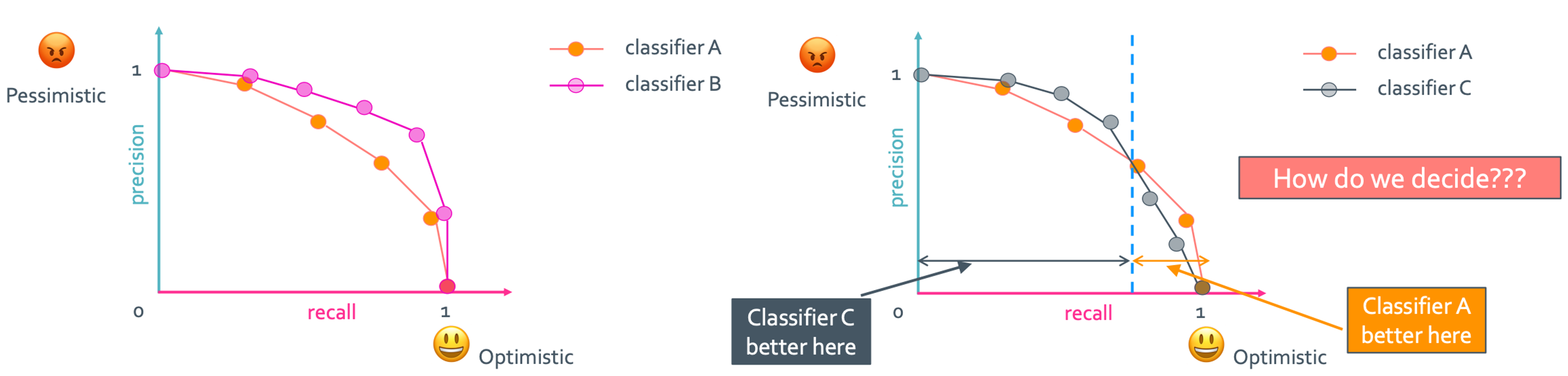
왼쪽의 경우 당연히 classifier B가 더 좋다는 것을 알 수 있다. 그런데 오른쪽의 경우는 어떻게 해야할까? 서로 좋은 부분이 번갈아서 나온다. 이를 해결하는 알고리즘이 몇개가 있다.

Compare algorithms

1. F1 measure
   이는 precision and recall의 harmonic mean을 구하는 것이다. 이는 단순한 평균보다 더 잘 대변한다.

   $\text{F1 measure} = \frac{2*\text{precision}*\text{recall}}{\text{precision}+\text{recall}}$

2. Area-under-the-curve(AUC)
   이는 아래의 면적을 비교해 면적이 더 큰 classifier가 더 좋은 classifier임을 구할 수 있다. 그래서 Best classifier의 면적은 항상 1이 나오게 된다.
3. Precision at K
   이건 그냥 상위의 K개만 가지고 precision의 값을 비교하는 것이다.

Summary

FP: 하지 말껄
FN: 할껄 -> 인생에서 이걸 후회하지 말고 꼭 시도해보라고 교수님이…
TP: 하기 잘했다
TN: 안하기 잘했다