ML - Lecture 12: Ensemble learning
우리가 앞에서 구한 classifier들은 꽤나 좋은 성능을 보여줬다. Variance가 낮고 빠르게 learning을 하는 장점이 있었다. 하지만 bias가 높게나온다는 단점이 있다. 왜냐하면 우리가 true error를 줄이기 위해 weak(simple) classifier를 선택했기 때문이다.
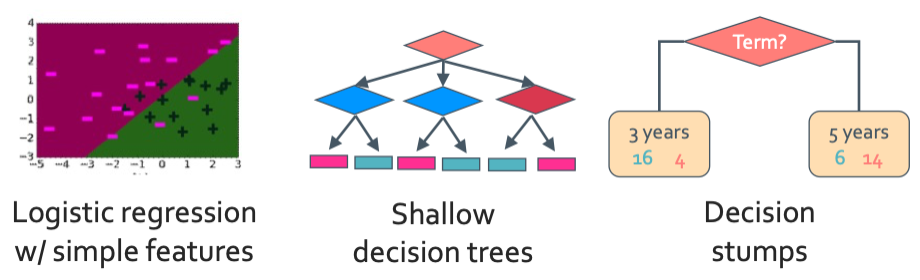
그럼 이러한 weak laerner들을 strong learner로 만들 방법이 없을까? 이걸 바로 ensemble learning: bagging & boosting을 통해 해결할 수 있다.
◼︎ Ensemble classifier
Ensemble model은 여러 simple classifier를 coefficient의 가중치에 따라 선형 결헙된 model이다. 우선 simple classifier는 $\hat{y} = f(x) = +1$ or $-1$이다. 그래서 나온 essemble model은 다음과 같다.
F($x_{i}$) = sign($w_1 f_1(x_i) + w_2 f_2(x_i) + ... + w_n f_n(x_i)$)
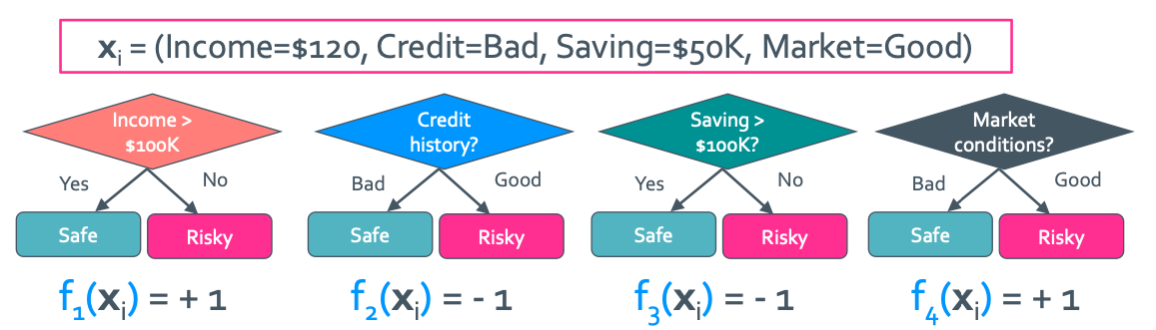
이런식으로 여러개의 simple classifier가 결합된 형태가 나온다. 그래서 최종 공식은 다음과 같다.
$\hat{y} = \operatorname{sign}(\sum_{t=1}^{T}\hat{w_t}f_t(x))$
◼︎ Bagging
Variance를 줄이는 model을 만들면 생기는 문제점이 있다.
- Training set이 하나
- 이렇게 training set이 하나밖에 없는데 어떻게 multiple model을 만들 수 있는 것일까?
그래서 나온것이 Bagging이다. BAGGing은 Bootstrap AGGregation으로 하나만 있던 training set을 통해 data set을 늘리는 방법이라고 생각하면 된다.
Bagging algorithm
주어진 N개의 training example을 가지고 있는 data set으로 random하게 순서를 바꾼 N개의 training example을 가지고 있는 D’을 만드는 것이다.
Random forests
Ensemble method는 여러 decision tree classifier로 이루어 져있다고 하였다. Random forest는 이 여러 tree들을 임의로 뽑아 tree를 새구성 하는 것이라고 생각하면 된다. 그래서 이 임의의 요소로 2가지를 나눈다.
- Bagging: training data의 sample을 random하게 뽑는 것
- Random vector: 모든 feature를 고려하는 것이 아닌 random하게 뽑은 일부의 feature로 split하는 것
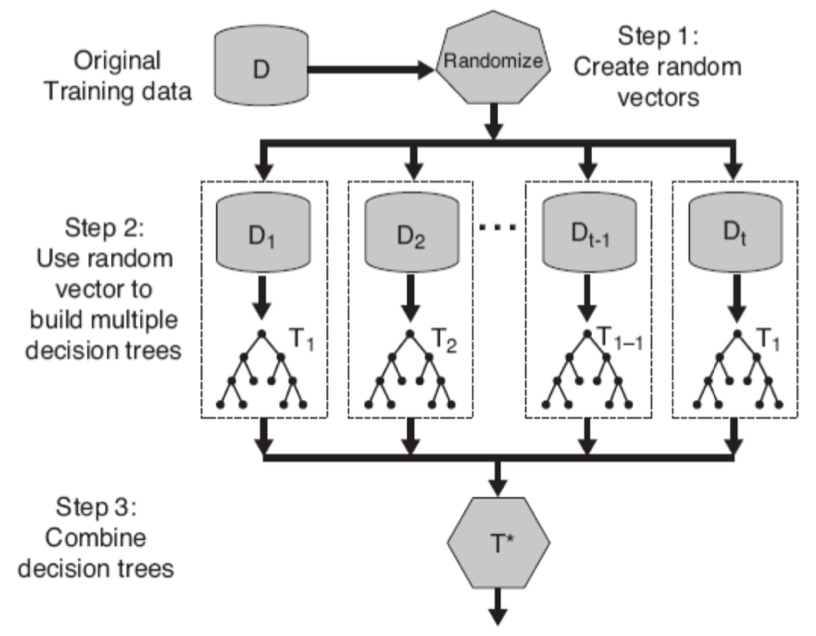
Bagging은 variance를 줄여주긴 한다. 하지만 bias를 줄이는 데는 별로 도움이 되지 않는다. 그래서 우리는 boosting을 통해 bias를 줄여주는 것이다.
◼︎ Boosting
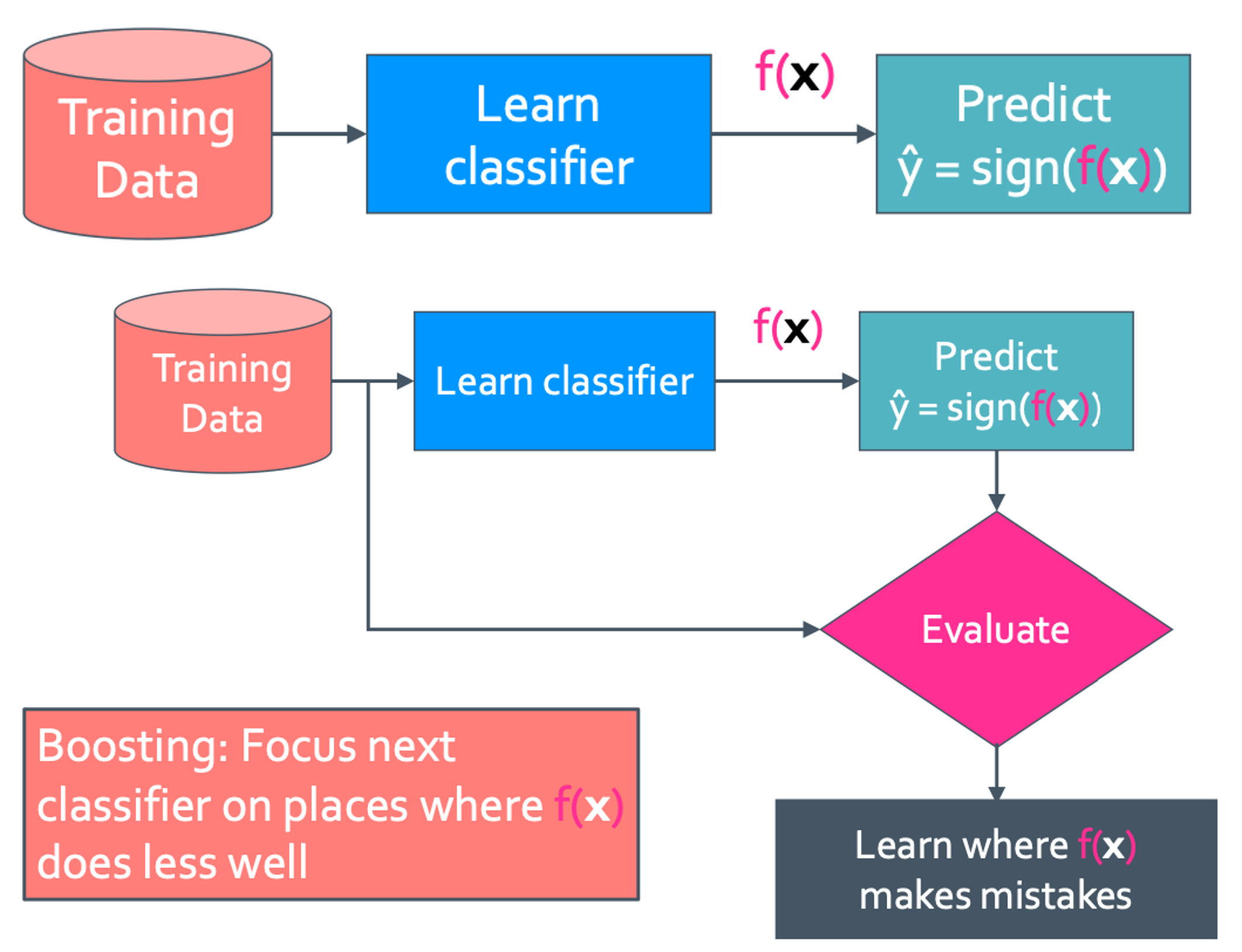
이렇게 simple classifier를 evaluating과정을 통해 어디가 틀렸는지를 알게 된다. 이 결과를 통해 가중치를 설정해 boosting을 하게 되는 것이다. 이 가중치는 weight의 $w_i$ 또는 $\alpha_i$로 설정한다. 그래서 맨 처음은 모든 가중치가 다 같은 1로 설정 한 다음 evaluating을 통해 정답(O)인 것은 중요도가 낮아서(↓) 가중치를 줄이고(↓), 틀린(X) 것은 중요도를 높이기(↑) 위해 가중치를 늘려주면(↑) 된다.
◼︎ AdaBoost
- 모든 점이 same weight를 가지게 함: $\alpha_1^i = 1/N$
- t = 1, …, T일때의 weight를 계산: $\alpha_i^t$, $\hat{w_t}$, $\alpha_i^{t+1}$
- $\hat{y} = \operatorname{sign}(\sum_{t=1}^T \hat{w_t}f_t(x))$
Computing coefficient $\hat{w_t}$
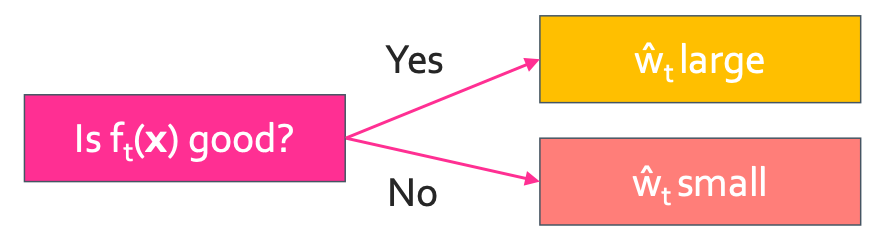
이렇게 $f_t(x)$를 평가하여 $\hat{w_t}$를 늘릴리 줄일지 결정하여 새로운 $f_t(x)$를 만드는 것이다. 이렇게 구한 가중치를 이용하여 classification error를 정의 할 수 있다. $f_t(x)$가 좋은 feature이면 가중치를 늘려줘야 할 것이고 좋지 않으면 낮춰줘야 한다.
$\operatorname{Weighted classification error}(\epsilon_t) = \frac{\operatorname{total weight of mistakes}}{\operatorname{total weight}} = \frac{\sum_{i=1}^{N} \alpha_i \mathbf{1}(\hat{y_i} \neq y_i) }{\sum_{i=1}^{N} \alpha_i}$
이렇게 error를 정의 했는데 그러면 $\hat{w_t}$은 어떻게 구할 수 있는 것일까? $\hat{w_t}$은 다음과 같다.
$\hat{w_t} = \frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t})$
Recompute weights $\alpha_{t+1}^i$
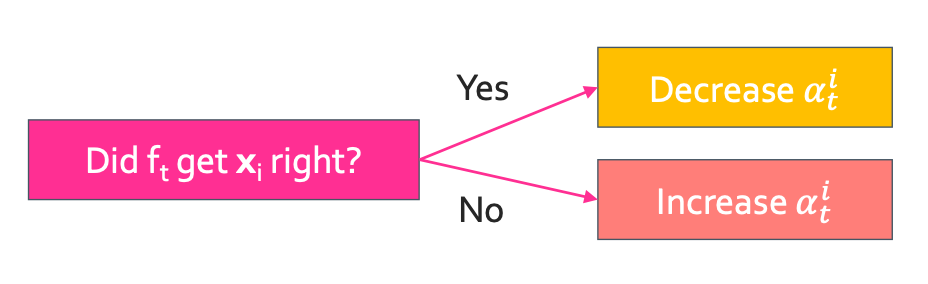
그 feature로 구한 $x_i$가 정답이면 중요도가 낮기 때문에 $\alpha_t^{i}$를 줄여주고 틀리면 중요도가 높아 $\alpha_t^{i}$를 높여준다.
그러면 $\alpha_{t+1}^{i}$는 다음과 같이 쓸 수 있을 것이다.
$\alpha_{t+1}^{i} = \begin{cases} \alpha_{t}^{i}e^{- \hat{w_t}}, \; \mathrm{if} \; f_t(x_i) = y_i \newline \alpha_{t}^{i}e^{\hat{w_t}}, \; \mathrm{if} \; f_t(x_i) \neq y_i \end{cases}$
$ = \alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}$
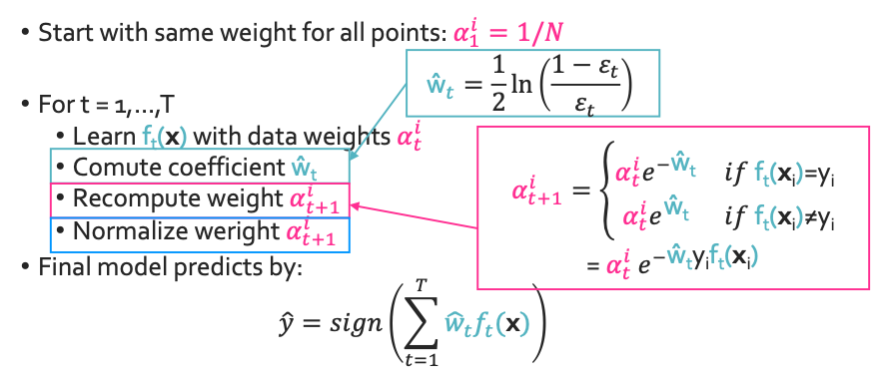
최종적으로는 이런 식들을 얻을 수 있다.
◼︎ Boosting convergence & overfitting
Overfitting
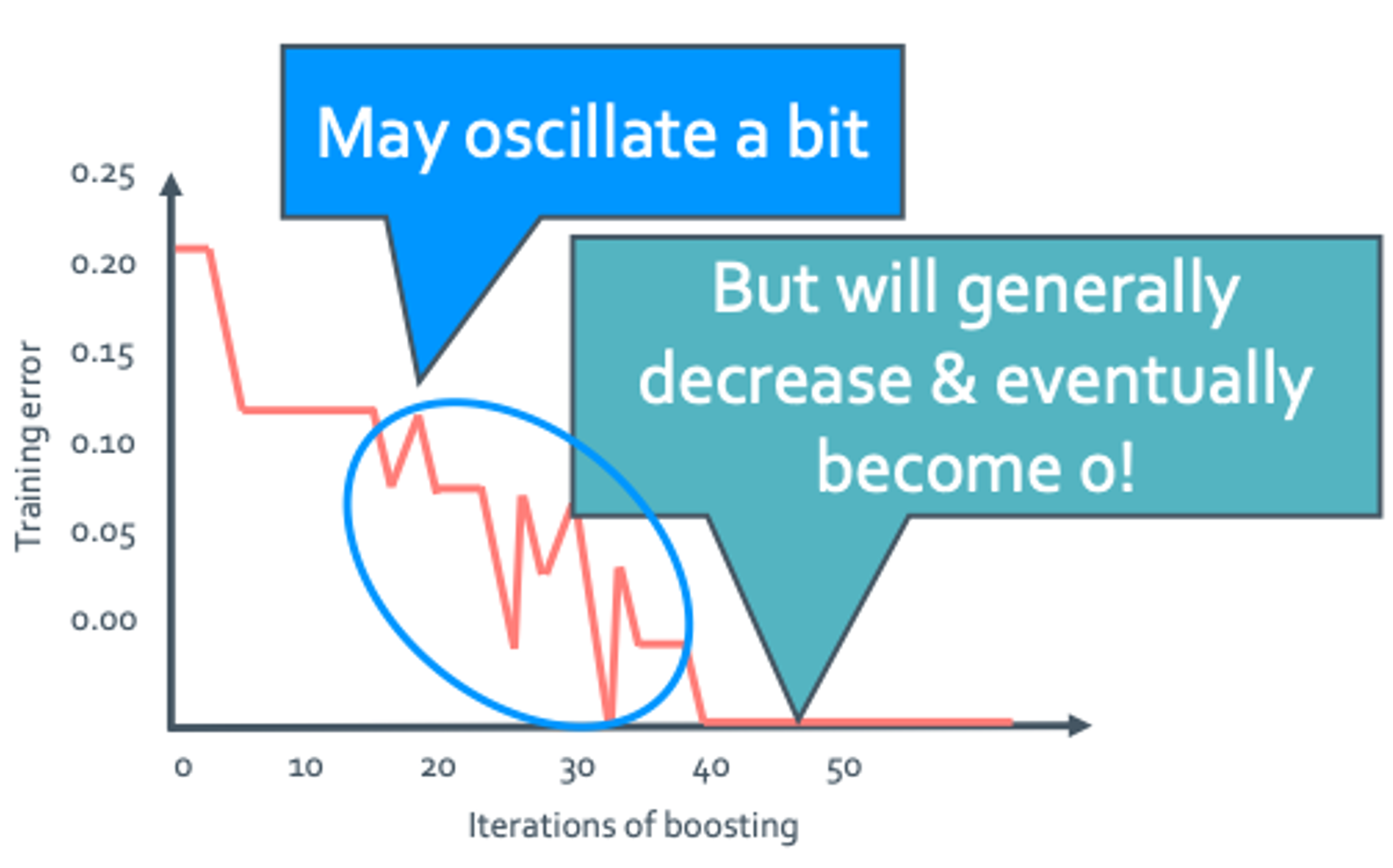
Iteration이 많아지면 결국 overfitting이 일어나게 된다.
Boosting convergence
우선 training error는 다음 부등호를 만족한다.
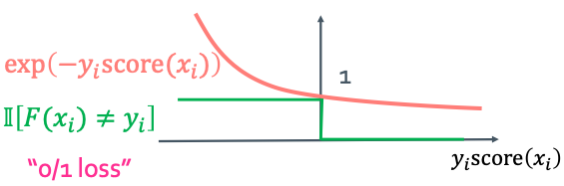
이렇게 나오는 $E_{train}$이 작은 것이 좋다. 그리고 수식에서 알 수 있듯 어떠한 최대값으로 converge하는 것을 계산해볼 예정이다.
그리고 항상 $ \operatorname{score}(x) = \sum_{t} \hat{w_t} f_t(x); Z_t = \sum_{i=1}^{N} \alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}$ 이다.
$\alpha_{t+1}^{i} = \frac{\alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}}{\sum_{i=1}^{N} \alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}} = \frac{\alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}}{Z_t}$ and $\sum_{i=1}^{N} \alpha_{t+1}^{i} = 1$을 만족
◆ $\frac{1}{N} \sum_{i=1}^{N} \operatorname{exp}(-y_i \operatorname{score}(x_i)) = \prod_{t=1}^{T} Z_t$의 증명
$\begin{align}
\alpha_{t+1}^{i} = \frac{\alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}}{\sum_{i=1}^{N} \alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}} = \frac{\alpha_{t}^{i}e^{- \hat{w_t} y_i f_t(x_i)}}{Z_t} \newline
\alpha_{t}^{i} = \frac{\alpha_{t-1}^{i}e^{- \hat{w_{t-1} y_i f_{t-1}(x_i)}}}{\sum_{i=1}^{N} \alpha_{t-1}^{i}e^{- \hat{w_{t-1} y_i f_{t-1}(x_i)}}} = \frac{\alpha_{t-1}^{i}e^{- \hat{w_{t-1}} y_i f_{t-1}(x_i)}}{Z_{t-1}}\newline
\alpha_{t+1}^{i} = \frac{\alpha_{t-1}^{i}e^{- \hat{w_t} y_i f_t(x_i) + \hat{w_{t-1}} y_i f_{t-1}(x_i)}}{Z_{t-1}} \newline
= \frac{\alpha_1^i e^{- y_i \sum_{t=1}^{T} \hat{w_t} f_t(x_i)}}{\prod_{t=1}^{T} Z_t} \newline
= \frac{(1/N) e^{- y_i \sum_{t=1}^{T} \hat{w_t} f_t(x_i)}}{\prod_{t=1}^{T} Z_t} \newline
\alpha_{t+1}^{i} \prod_{t=1}^{T} Z_t = \frac{1}{N} e^{-y_i \operatorname{score}(x_i)} \newline
\therefore \prod_{t=1}^{T} Z_t = \sum_{i=1}^{N} \alpha_{t+1}^{i} \prod_{t=1}^{T} Z_t = \frac{1}{N} \sum_{i=1}^{N} e^{-y_i \operatorname{score}(x_i)}
\end{align}$
◆ $\hat{w_t} = \frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t})$의 증명
$\begin{align}
Z_t = \frac{1}{N} \sum_{i=1}^{N} \alpha_t^i e^{- \hat{w_{t}} y_i f_{t}(x_i)} \newline
= \sum_{f_t(x_i) \neq y_i} alpha_t^i e^{+ \hat{w_t}} + \sum_{f_t(x_i) = y_i} alpha_t^i e^{- \hat{w_t}} \newline
= \epsilon_t e^{+ \hat{w_t}} + (1-\epsilon_t)e^{- \hat{w_t}} \newline
\frac{\partial Z_t}{\partial \hat{w_t}} = \epsilon_t e^{+ \hat{w_t}} - (1-\epsilon_t)e^{- \hat{w_t}} = 0 \newline
ln \epsilon_t + \hat{w_t} = ln(1-\epsilon_t) - \hat{w_t} \newline
\therefore \hat{w_t} = \frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t})
\end{align}$
◆ $\prod_{t=1}^{T} Z_t \leq e^{-2\delta^2 T}$의 증명
우선 classifier는 최소한 random하게 뽑는(1/2)보다는 더 좋아야 한다. 그래서 $\epsilon_t < 0.5$라고 한다. 그래서 다음과 같은 식을 얻을 수 있다.
$E_{train} = \frac{1}{N} \sum_{i=1}^{N} \mathbf{1}(F(x_i) \neq y_i) \leq \prod_{t=1}^{T} Z_t \leq e^{-2\delta^2 T}$ where $\delta > 0, \delta_t \geq \delta, 0 < \delta_t < 0.5, \epsilon_t = 0.5 - \delta_t$
$\begin{align}
Z_t = \epsilon_t e^{+ \hat{w_t}} + (1-\epsilon_t)e^{- \hat{w_t}} \newline
= \sqrt{4 \epsilon_t(1-\epsilon_t)} \newline
= \sqrt{4 (\frac{1}{2} - \delta_t)(\frac{1}{2} + \delta_t)} \newline
= \sqrt{1 - 4 \delta_t^2} \leq e^{-4 \delta_t^2 /2} = e^{-2 \delta_t^2} \newline
\therefore \prod_{t=1}^{T} Z_t \leq \prod_{t=1}^{T} e^{-2 \delta_t^2} = e^{-2 \delta_t^2 T} (\because \delta_t \geq \delta)
\end{align}$