ML - Lecture 11: Decision tree
Decision tree도 classification에 속하는 supervised learning이다. 하지만 조금 다른 특성이 있다. 이걸 이해하기 위해서는 우선 parametric과 nonparametric model의 차이를 알아야 한다.
◼︎ Parametric & nonparametric approaches
-
Parmetric model
모델의 parameter의 수가 정해져(fixed) 있다. 그리고 data distribution을 정할 수 있다. 장점으로는 low complexity를 가지고 단점으로는 not flexible하다는 것이다. 즉, parametric modle은 데이터가 특정 분포를 따른다고 가정하고 데이터가 얼마나 많던간에 parameter가 고정되어 있기 때문에 속도가 빠르지만 간단한 문제를 푸는데에 더 적합하다.
ex) Linear regression, logistic regression, perceptron, linear discriminant analysis, k-means, (simple)neural networks -
Non-parametric model
모델의 parameter의 수가 학습 데이터의 크기(amount of training data)에 따라 달라지고 data distribution이 정해져 있지 않다. 장점은 flexibility와 distribution에 대한 적은 가정을 사용하지만 단점으로는 high complexity를 가진다. 즉, 데이터가 특정 분포를 따르지 않으므로 paramter가 정해져있지 않아 data에 대한 사전지식이 없을 때(no prior knowledge) 유용하게 사용될 수 있다.
ex) Decision tree, locally weighted(structured) regression models, PCA, Gaussian process, deep neural networks
◼︎ Predicting
대출을 빌려줄만한 신용이 있는 사람인지 판단하는 것으로 예시를 들어보려고 한다. 그 사람의 신용은 카드 기록 내역, 수입, 개인정보 등등으로 평가를 매길 수 있을 것이다. 그러면 이 각각의 평가 종목으로 그 사람에게 대출을 빌려줘도 safe할 지 risky할 지 판단이 될 것이다. 이걸 safe는 +1 risky는 -1로 classifier model을 만들 수 있을 것이다. 그런데 지금 이 상황은 이런 항목들이 여러개가 있는거다. 그래서 tree형태의 dicision tree를 그릴 수 있게 된다.
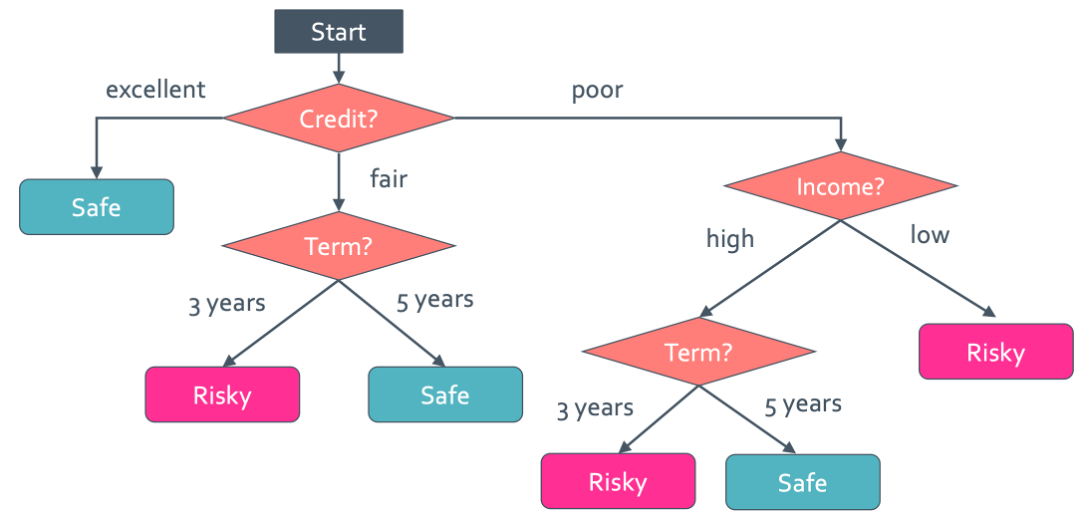
이 tree에서 만약 credit은 poor하지만 income은 high고 termdms 5년이라고 하면 safe에 해당되기 때문에 빌려줄 만 하다는 것이다.
◼︎ Decision tree learning task
우선 decision tree는 supervised learning이기 때문에 정답이 존재한다. 그래서 우리의 모델이 safe혹은 risky라고 판단한 것을 metric을 통해 신뢰도를 봐야 한다. 그래서 error가 생기게 될 텐데 이를 best possible value라면 error는 0이고 worst possible value면 1이 되게 만들 것이다. 이 가정에 의해 만든 error의 공식은 다음과 같다.
$\operatorname{Error} =\frac {\operatorname{Number of incorrect prediction}}{\operatorname{Number of examples}}$
그러면 우리는 가장 좋은 트리는 어떻게 찾아야 하는 것일까? 일단 decision tree의 possible tree는 exponential하게 엄청 많을 것이다. 그래서 smallest decision tree를 learning하는 것은 NP-hard problem이다.
- NP-hard problem: Nondeterministic Polynomial, 다항 시간안에 풀 수 없는 문제. 즉, 시간이 무지하게 오래걸리는 문제라는 것
◼︎ Greedy decision tree learning
우선 모든 data를 다 고려해볼 것이다. 예시로는 N = 40이고 feature는 3개인 대출 신용도 case로 들어보자.
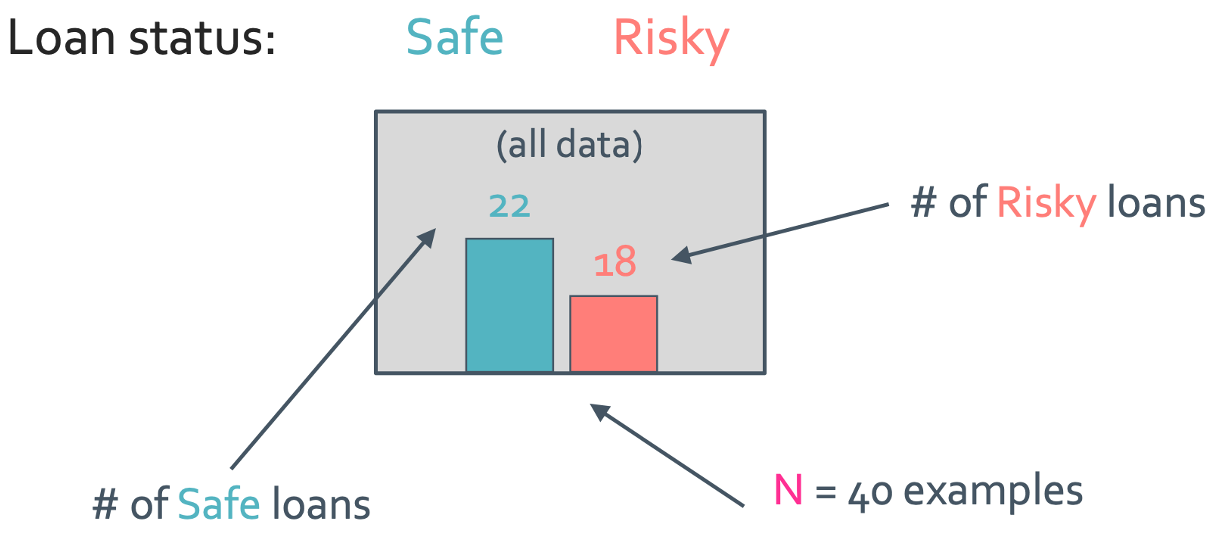
이건 최종적으로 safe 한 사람을 22명 risky한 사람을 18명이라고 판단한 것이다. 일단 tree는 복잡하니 tree말고 decision stump부터 보겠다. decision stump는 아주 간소화된 single level tree를 뜻한다. 아래에는 credit으로만 판단한 decision stump를 보여줄 것이다.

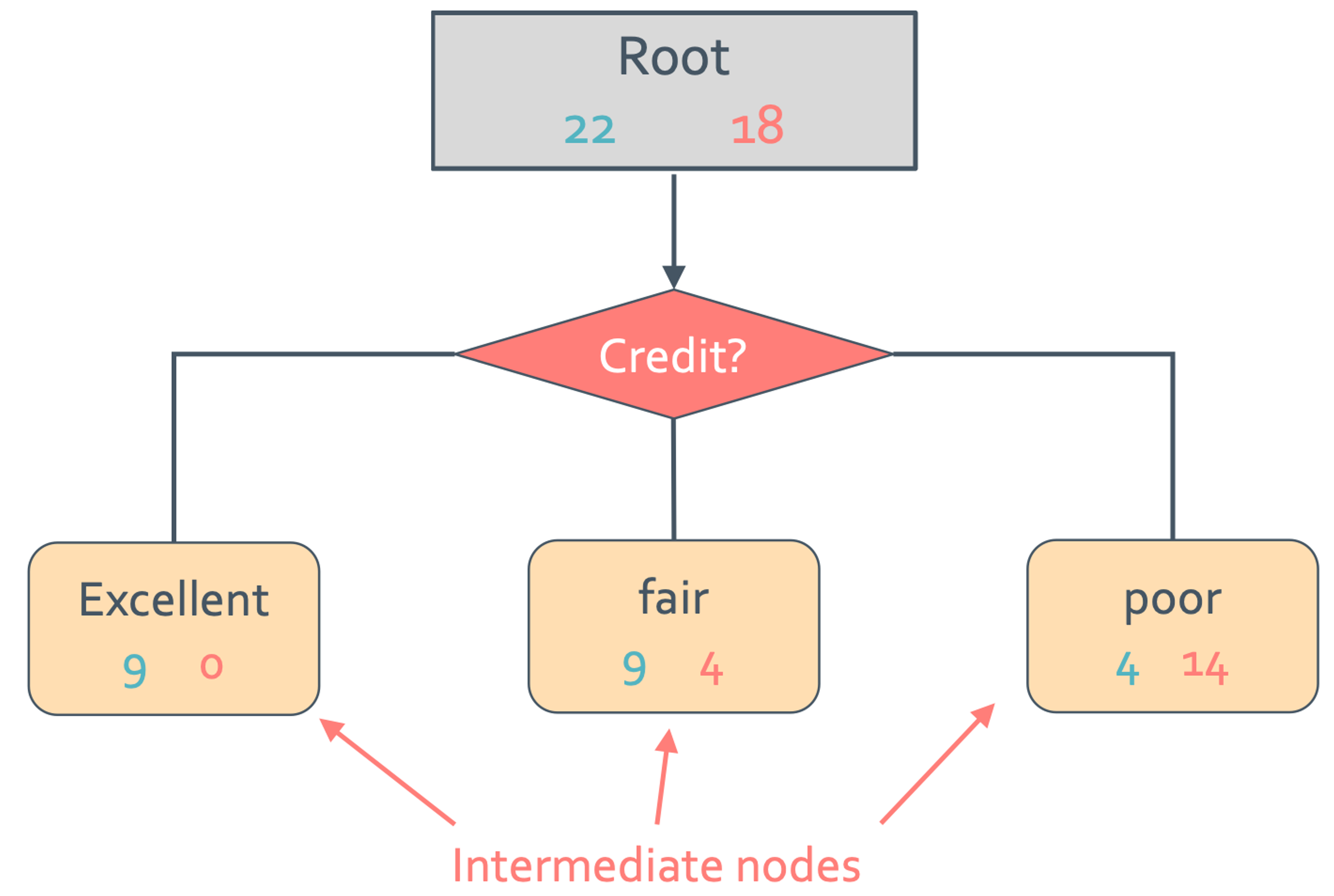
아래의 node들을 intermediate node라고 한다. 이 intermediate node에서 majority value를 $\hat{y}$으로 설정할 것이다. 그래서 위의 그림에서 excellent일 때 $\hat{y}$= safe, fair일 때 $\hat{y}$ = safe, poor일 때 $\hat{y}$ = risky일 것이다.
◼︎ Selecting best feature to split on
위에서 알려준 stump는 어떤 feature를 선택하느냐에 따라 여러 개의 decision stump가 발생할 것이다. 그럼 이 stump들 중 effective한 것을 어떻게 구할 수 있을까? 바로 우리가 정의했던 error로 판단을 하게 된다.
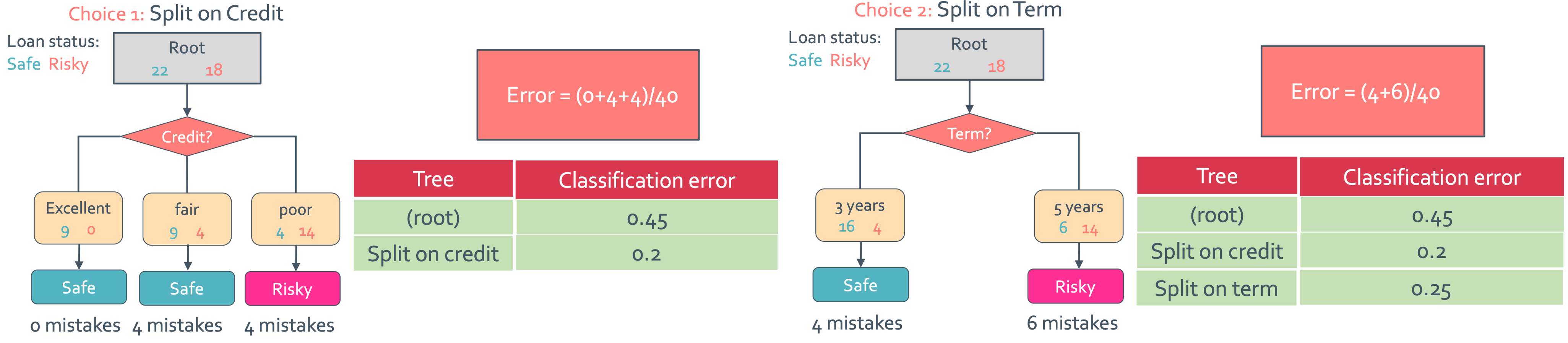
위의 그림을 보면 root에서는 18/40 = 0.45, credit 기준일 때 (4+4)/40 = 0.2, term 기준일 때 (4+6)/40 = 0.25이므로 credit 기준일 때 error가 제일 적다.
Feature split selection algorithm
그래서 어떤 feature를 사용해야하는지 알아내는 알고리즘을 만들어 볼 것이다. 우선 data의 subset은 M으로 주어지고 이것은 tree 의 node와 같다.
- feature $h_{i}(x)$를 구한다.
- $h_{i}(x)$에 맞게 M을 split한다.
- Error를 계산한다
- Lowest error를 가지는 $h^{*}(x)$를 구한다.
◼︎ Recursion & Stopping conditions
근데 뭔가 이상한게 있다. 우리는 decision stump를 배우려는 것이 아니라 decision tree가 궁금한 것 아닌가? 그런데 decision stump부터 설명해야 하는 이유가 뭔가 있을 것이다. 그 이유는 recursive stump learning의 결과가 decision tree learning이기 때문이다. Stump를 재귀적으로 선택하면서 error가 가장 작은 최종 tree를 구하는 것이다.
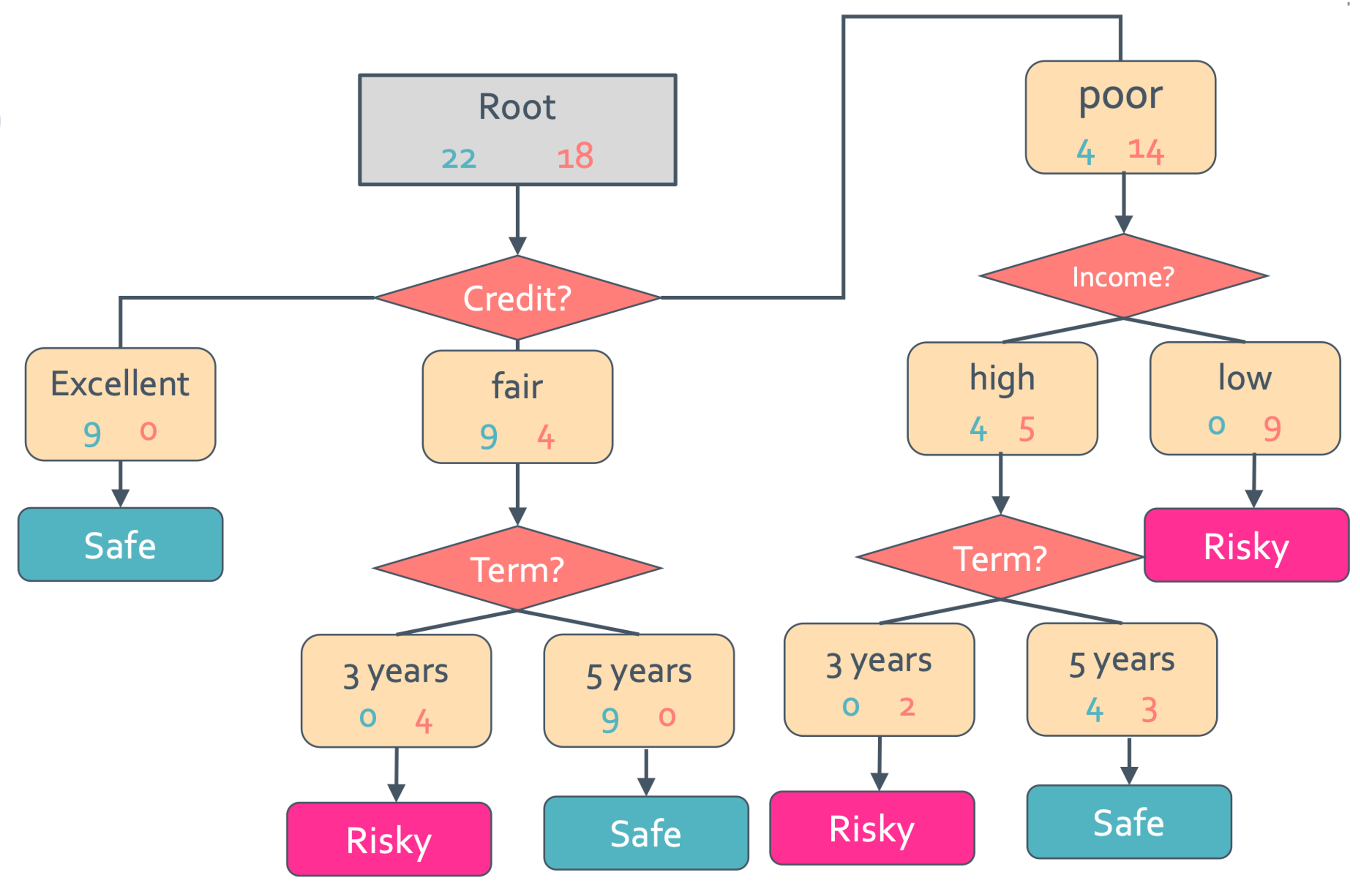
이렇게 error가 크게 나오는 node들은 다른 feature를 적용시켜 stump를 만들어주고 그것을 계속 반복 시키는 것이다.
- Pick best featue to split on, error작게 나오는 feature 선택하기
- learn decision stump with this split, stump 만들기
- For each leaf of decision stump recures, mistake가 나오는 leaf를 stump로 만드는 재귀 진행 (1번으로 다시)
이건 알겠는데 어디까지 recursion을 해야할까? 언제 멈춰야 하지?
일단 간단하게 생각할 수 있는것은 condition 3 = stopping when training error doesn’t improve 즉, error가 줄지 않는 시점부터 멈추기이다. 예시로는 어떤 feature를 선택하던 error가 똑같이 나오는 경우일 것이다.
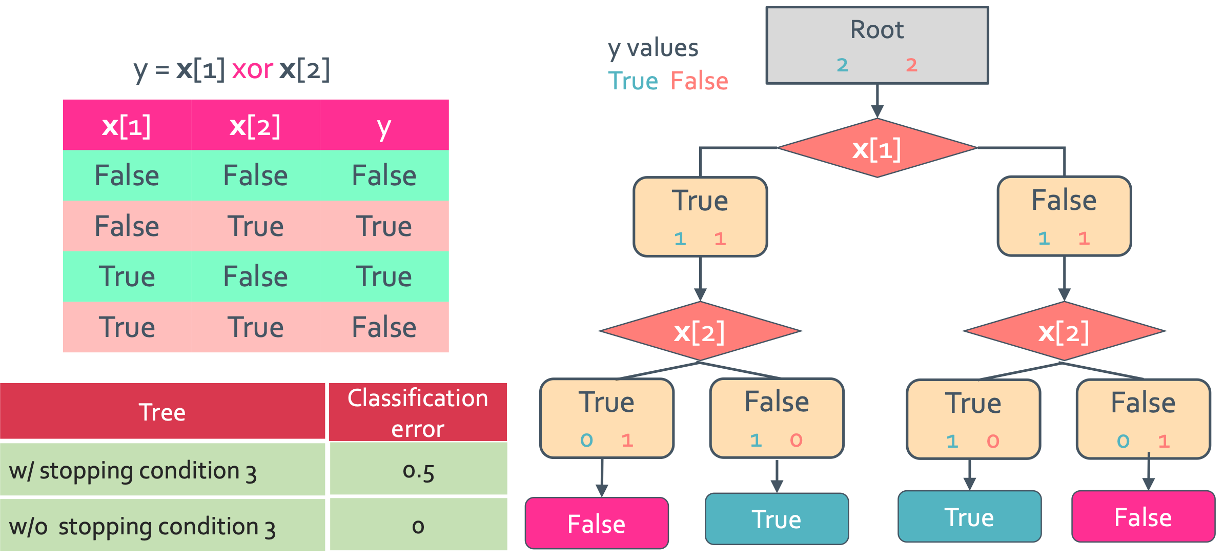
이것은 condition 3의 반례이다. condition 3에 의하면 x[1]을 사용하던 x[2]를 선택하던 error가 2가 나와서 recursion이 중지되어 최종 error는 0.5가 나오게 되지만 위의 경우처럼 그냥 끝까지 적용하면 error가 0이 되는 결과를 얻을 수 있다. 그래서 condition3가 무조건 recommend되지는 않는다.
◼︎ Decision tree leaning: Real valued features
이제는 그 feature를 통해 나온 값이 앞에서 본 결과처럼 descrete하지 않고 continous한 값이면 어떻게 해야 할까? 이는 간단하게 threshold를 사용하는것으로 해결할 수 있다.
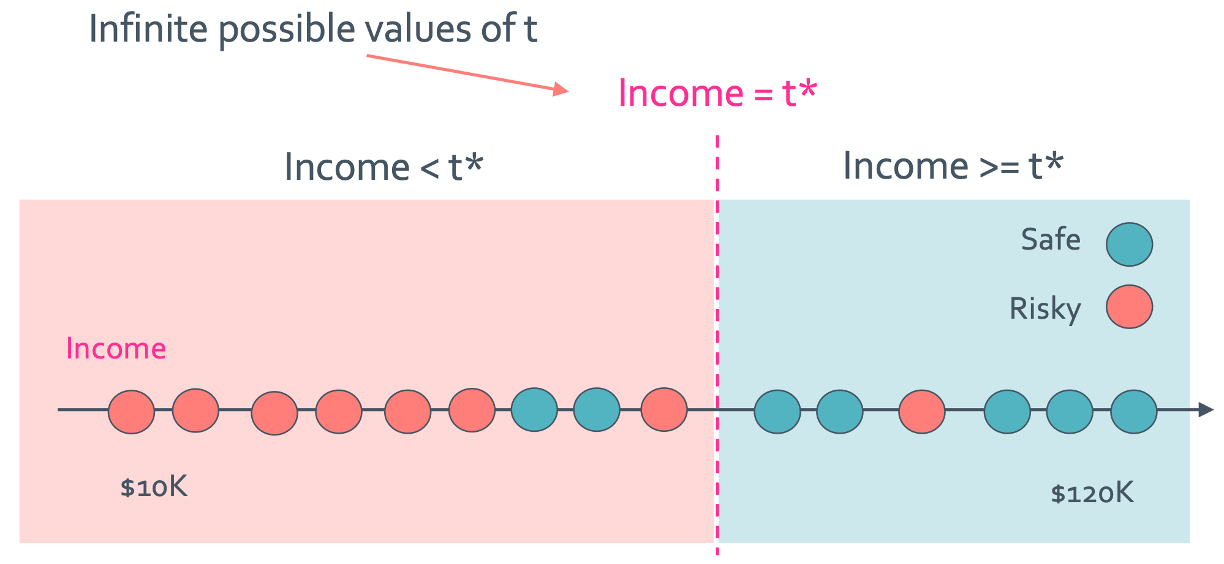
이렇게 classification error가 가장 작아지는 threshold($t^{*}$)로 나눌 수 있게 되는 것이다.
Threshold split selection algorithm
- Sort the value of a feature $h_{j}(x)$, $h_{j}(x)$를 기준으로 값 분류
- {$v_1, v_2, …, v_n$} 을 denote sorted value로 둔다
- For i = 1, …, N-1
- $t_i$ =($v_i + v_{i+1}$)/2 로 설정
- $h_{j}(x) \leq t_i$만족하는 classification error 계산
- $t^{*}$를 lowest classification error값을 갖는 걸로 선택
이것을 visualize하면 이런식으로 나올 것이다.
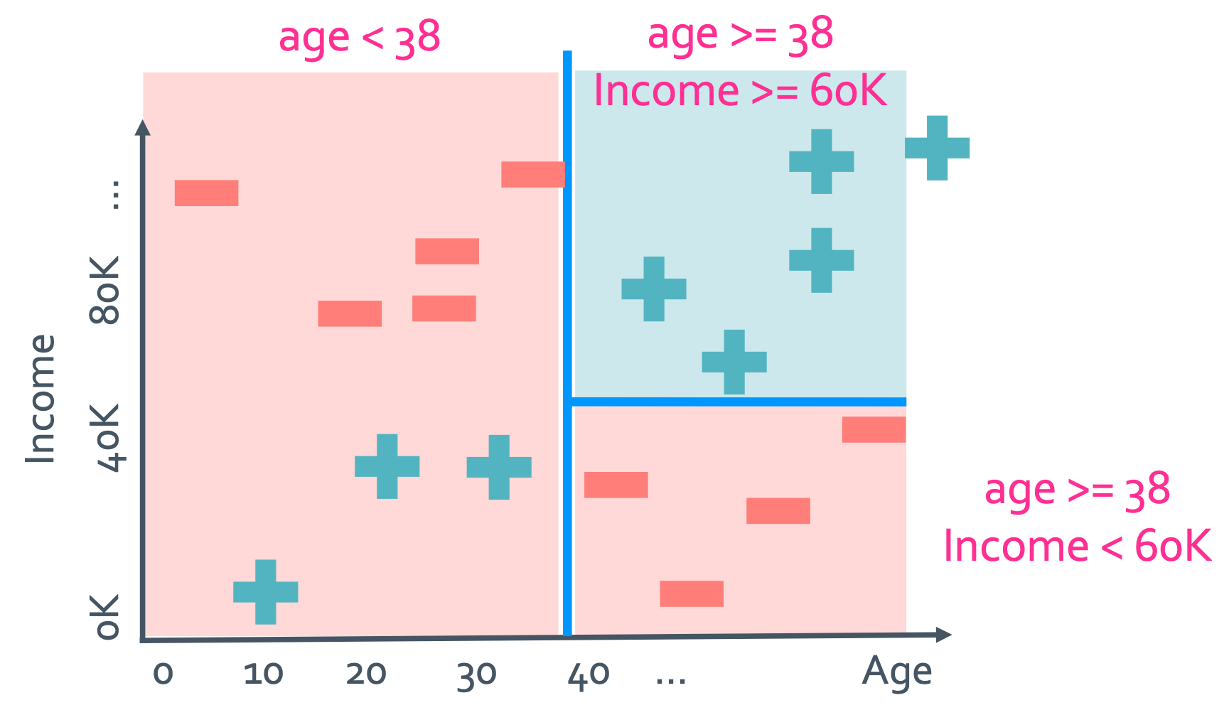
그래서 이 decision tree의 첫 stemp는 age에 의해 결정되고 그 다음 stemp는 income일 것이다.
◼︎ Decision tree vs logistic regression
근데 위에서 본 그림은 되게 logistic regression과 비슷한게 느껴질 것이다. 그런데 둘의 비교 그림을 보면 확실히 차이점이 이해가 갈 것이다.
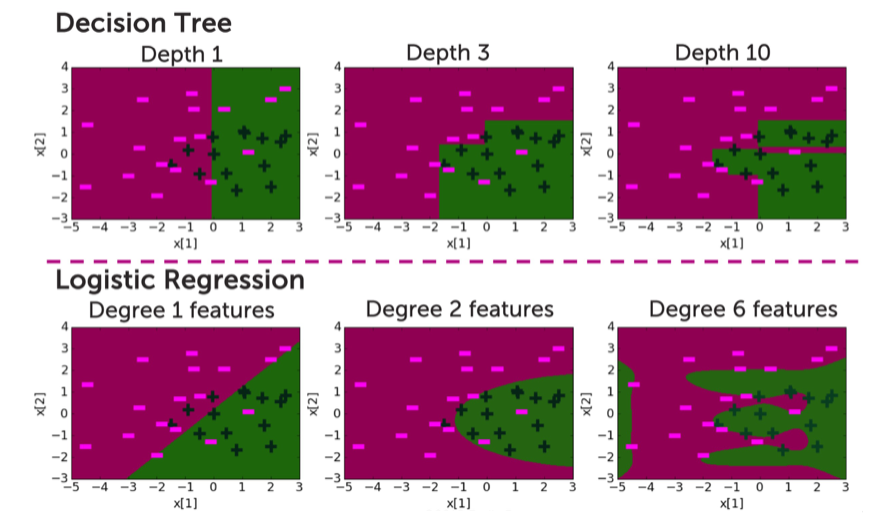
Decision tree는 직각으로 잘리는 반면 logistic은 polynomial하게 잘리고 있는 것을 확인할 수 있다.
◼︎ Overfitting in decision tree
Logistic regression에서 degree가 너무 커져버리면 overfitting이 일어난다는 것을 기억 할 것이다. 이와 같이 decision tree또한 depth가 증가함에 따라 overffiting이 일어나게 된다. Training error는 줄어들겠지만 과적합모델이 되기 때문에 이를 해결시켜줘야 한다. 그래서 다음의 두 가지 방법을 사용한다.
Two approaches to picking simpler trees
- Early Stopping(일찍 정지) : tree가 너무 complex해지기 전에 멈추기
- Pruning(가지치기) : 온전한 tree를 만들고 가지를 잘라내기 → 이게 더 좋은 방법이다
Early stopping
원래 tree의 성장이 멈추는 조건은 target value가 똑같아 지거나 feature를 다 써버리면 정지되게 된다. 하지만 early stopping은 다음과 같을 때 정지하게 된다.
- 트리 깊이 제한: max_length 설정 → 일정 이상으로 커지지 않게 고정
- Classification error를 별로 줄이지 못한다면 정지
- Data point가 너무 적을 때 노드를 분할 X
우선 max_length를 찾는 것 자체가 쉽지 않고 필요없는 split을 하지 않아도 된다는 장점에 반해 좋은 feature의 spit을 놓칠수도 있는 확률이 있다.
Pruning
Pruning은 일단 복잡한 tree를 만든 후 가지를 쳐서 간단하게 만들어버리는 방법이다. 우선 아래의 그래프를 봐보자.
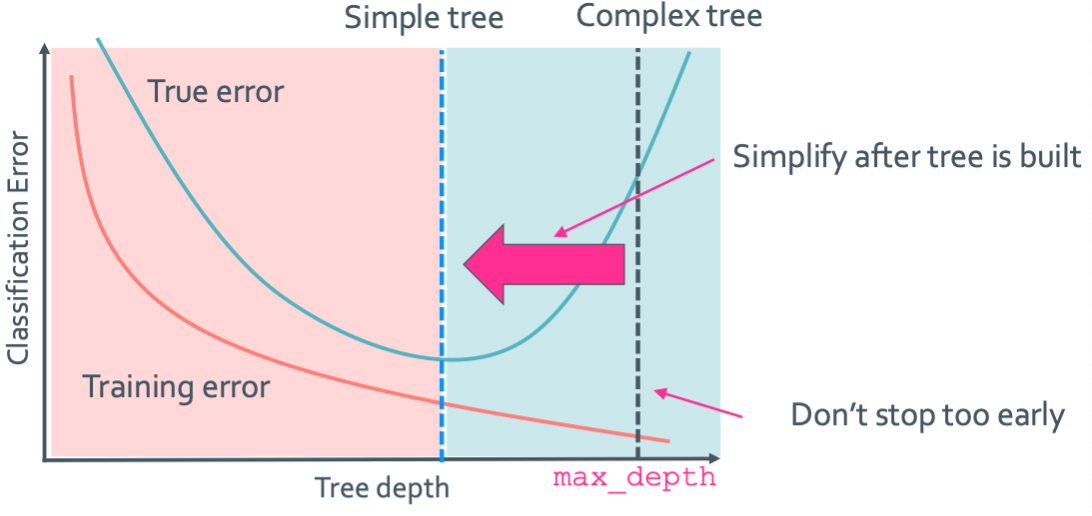
Tree depth가 늘어나야 training error가 줄어들지만 너무 커지면 overfitting에 의해 true error가 늘어나는 것을 확인할 수 있다. 그리고 pruning은 complex tree를 만들어서 나온 max_depth를 옮겨서 simple tree로 만들고 true error를 줄일 수 있다.그러면 이 것을 수치화 해서 좋은 depth를 구할 수 있도록 해 보자.
그래서 cost 함수를 다음과 같이 정의 할 것이다.
Total cost = measure of fit + measure of complexity
그리고 우리는 L(T) = leaf의 개수라고 할 것이다. L(T)가 너무 크면 overfitting이 되고 너무 작으면 classification error가 날 것이다. 그래서 이것을 regularization처럼 만들면 다음과 같이 쓸 수 있다.
Total cost C(T)= Error(T) + $\lambda$ L(T)
이렇게 구한 error는 prun전과 후를 비교해 만약 prun을 한 것의 cost가 더 작으면 pruning을 적용하면 되고 아니면 그대로 두면 된다.