CA - chapter 5 Large and Fast: Exploiting Memory Hierarchy

이제 우리는 전체적인 CPU의 구조에 대해 이해할 수 있게 됐다. 그런데 우리가 자세히 다루지 않고 계속 사용하던 것이 있다. 바로 memory이다. gate나 mux등을 통해 많은 것을 만들 수 있지만 저장공간에 대한것은 아무 설명 없이 그냥 사용했다. 이번 장에는 이 memory가 그래서 실제로 어떻게 구성돼 있는지에 대해 다뤄볼 것이다.

◼︎ Memory hierarchy analogy

도서관을 예시로 들어볼까 한다. 우선 내가 도서관에서 논문을 쓰고 있다고 가정하면 나는 processor가 되는 것이다. 그리고 도서관은 disk가 될 것이다. 왜냐하면 용량은 매우 크지만 어느 책(자료)를 찾기에는 오래걸리기 때문이다. 그리고 이 도서관안에 있는 책장들은 memory(RAM)라고 할 수 있을 것이다. 그리고 내가 올려둔 책이 있는 책상은 cache가 될 것이다. 매우 빠르게 접근 가능하지만 용량이 크지 않은 것이다.

Principle of Locality

프로그램은 전체 메모리중 일부분만 자주 접근한다. 즉, 좋은 책이 있으면 그 책을 자주 사용하게 되는 것이다. 이것을 locality라고 한다.

• Temporal locality(시간적 지역성): 어떤 data가 한 번 사용되면 다시 사용될 가능성이 높다.
• Spatial locality(공간적 지역성): 어떤 data가 사용되면 그 근처 주소의 data도 사용될 가능성이 높다.

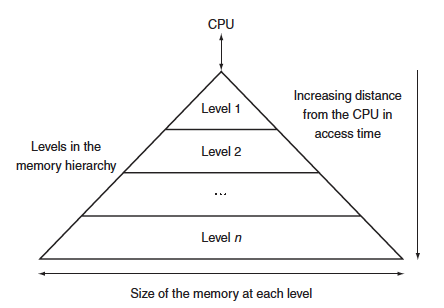
이렇게 memory는 locality를 띠기 때문에 memory hierarchy(메모리 계층구조)를 이용하게 되는 것이다. 메모리는 석로 다른 속도와 크기를 갖는 여러 계층의 메모리고 구성되어 있기 때문에 locality를 이용하면 더 효율적으로 사용할 수 있게 된다.

Speed	Processor	Size	Cost ($/bit)	Current Technology
Fastest	Memory	Smallest	Highest	SRAM (e.g., Cache)
	Memory	Medium	Medium	DRAM (Main Memory)
Slowest	Memory	Biggest	Lowest	Magnetic Disk or Flash Memory

CPU와 멀어질수록 느리지만 용량은 커지고 값이 싸지게 되는 것이다.

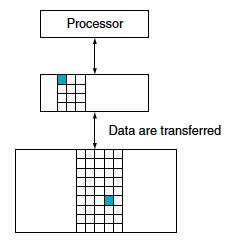
이렇게 한 쌍의 메모리 계층에는 상위 계층과 하위 계층이 있다. 각 계층 안의 정보가 존재하는 기본 단위를 블록혹은 라인이라고 한다.

용어

• Block(블록, 라인): 정보의 최소 단위
• Hit(적중): 프로세서가 요구한 데이터가 상위 계층의 블록에 존재할 때
• Miss(실패): 상위 계층의 블록에 존재하지 않을 때
• Hit rate(hit ratio, 적중률): 상위 계층에서 hit할 확률 = 1 - miss rate
• Hit time(적중시간): 상위 계층을 접근하는데 걸리는 시간
• Miss penalty(실패 손실): 하위 계층에서 해당 블록을 가져와서 상위 계층 블록과 교체하는 시간 + 그 교체된 블록을 프로세서로 보내는데 걸리는 시간

◼︎ Basics of caches(캐쉬의 기본)

Cache는 CPU와 main memory사이에 있고 locality of access에서 큰 장점을 가지게 된다.

만약 캐시에 최근 접근한 $X_1, X_2, X_3, … , X_{n-1}$이 존재하고 $X_{n}$을 요청했다고 하면 이 요청은 miss를 발생시키고 memory에서 $X_{n}$을 캐시로 가져오게 된다.

Direct mapped

우선 캐시 내에 데이터가 있는지 알아야하고 만약 있다면 찾을 수 있어야한다. 이를 위해 위치를 할당하는 가장 간단한 방법은 direct mapped(직접 사상)이다.

$(\mathtt{Memory\, block\, address}) \; \mathrm{MODULO} \; (\mathtt{Number\, of\, cache\, blocks\, in\, the\, cache})$

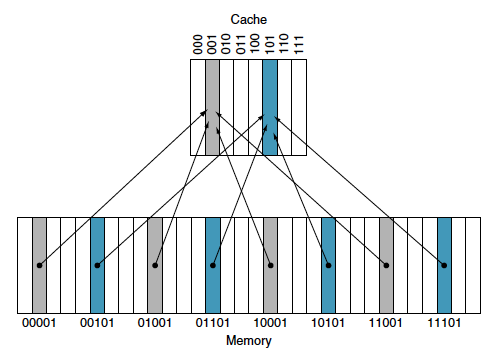
이 예시를 보면 8개의 캐시 블럭이 있다. 그래서 modulo 8인 것이고 파란색과 회색의 엔트리가 나눠지게 되는 것이다. 이렇게 되면 서로 같은 메모리 주소들이 같은 캐시 블록에 매핑될 수 있다는 문제가 있다.

• Tag: 태그는 캐시 내의 워드가 요청한 것인지 아닌지 식별하는데 필요한 주소 정보를 가지고 있고 캐시 인덱스로 사용되지 않은 주소의 상위 상위 부분 비트들로 구성된다. 위의 경우에서는 앞의 2비트가 tag가 된다.
• Valid bit(유효비트): 비트가 0이면 엔트리에 유효한 블록이 없는거로 간주

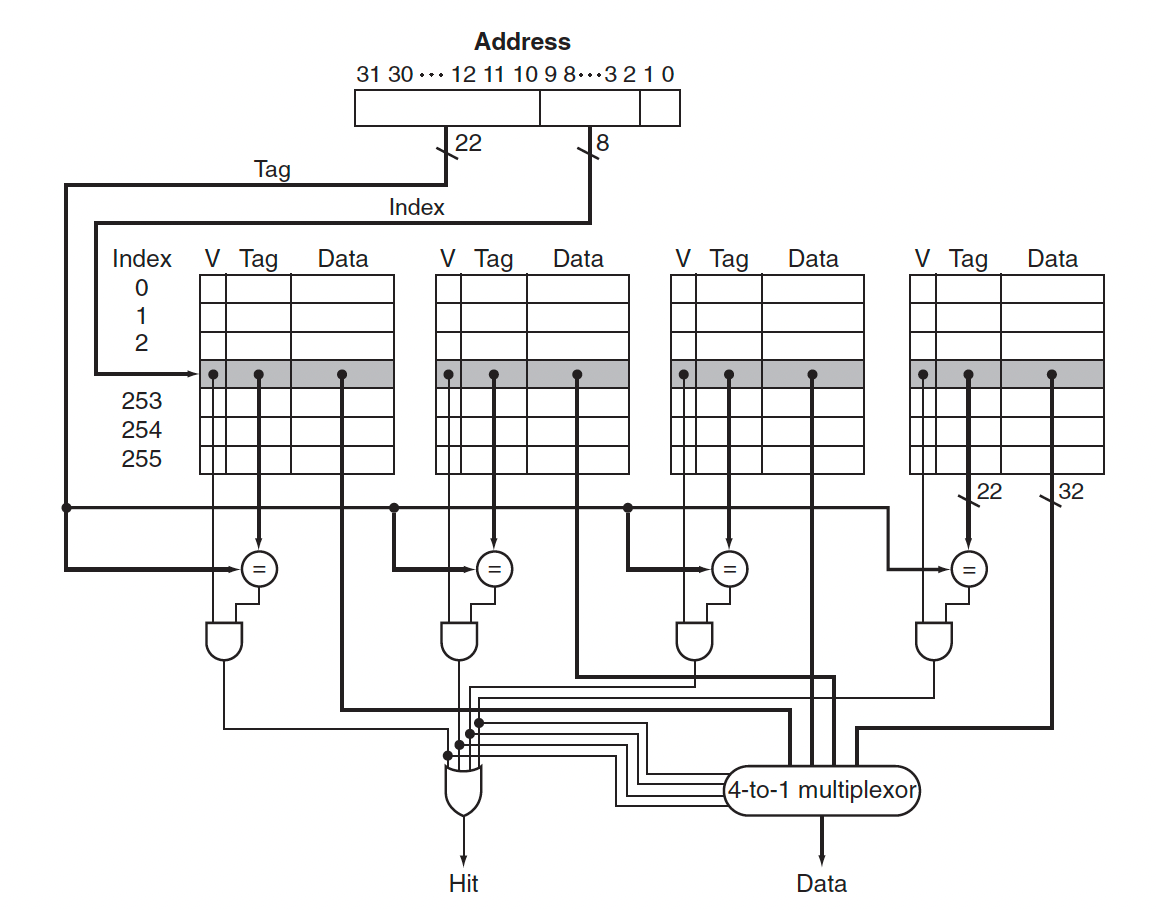
Accessing a cache(캐시 접근)

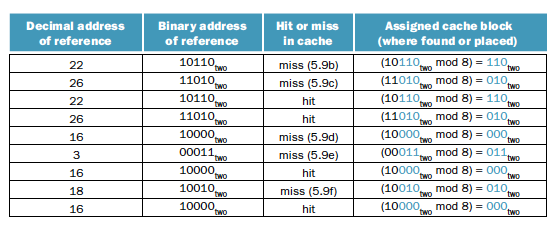
이 예시를 보면 우선 cache의 index에 해당되는 곳에 data가 없으면 miss가 일어나게 된다. 만약 data가 있고 tag가 같으면 hit를 하게 되지만 tag가 다르면 이것도 miss로 친다.

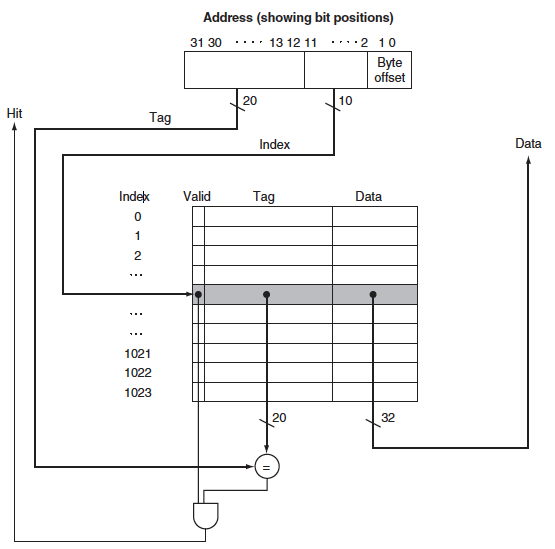
이 캐시에는 1024워드(4 KiB)가 있다. 주소는 32비트일 때 중간의 10비트는 캐시를 인덱싱하는데 쓰이고 나머지 20비트는 태그와 비교하는데 쓰인다. 이 두 시그널이 모두 1이어서 and의 결과값이 1이어서 hit가 되면 나오는 data를 사용하면 되고 0이면 miss이기 때문에 update 해야 한다.

Cache size

32비트의 주소가 있고 캐시에 $2^n$개의 블록이 있으면 n비트가 인덱스로 사용된다. 캐시 블록의 크기(data의 크기)는 $2^m$word($2^{m+2}$ byte)이면 tag의 크기는 $32 - (n+m+2)$가 된다. 그러면 캐시의 전체 비트수는

$2^n \times$(블록 크기 + 태그 크기 + 유효비트 크기)

이다. 그래서 이 캐시의 전체 비트 수는 $2^n \times$($2^m \times 32$ + $(32-n-m-2)$ + 1)이다.

Example 1

64비트의 주소로 16KB의 데이터와 4-word block이다.

블록의 개수는 4096/4=1024($2^{10}$)개의 블록이 있다. 각 블록에는 $4 \times 32 = 128$bit의 data가 있고 (64-10-2-2)=50비트의 태그가 있따. 그래서 전체 캐시의 크기는 $2^10 \times$($2^2 \times 32$ + $(64-10-2-2)$ + 1)이다.

Example 2

블록크기가 16byte이고 block의 개수가 64개인 캐시에서 바이트 주소 1200은 몇 번 블록에 direct되나?

$\frac{1200}{16} = 75$번째 블록에 위치할 것이고 이는 $75 modulo 64 = 11$에 direct될 것이다.

Miss rate vs Block size

Block이 커질수록 spatial locality 때문에 miss rate가 줄어드는 것은 사실이지만 miss penalty가 늘어난다는 단점이 존재한다. Miss는 안 나지만 전송시간이 너무 오래걸리게 되는 것이다.

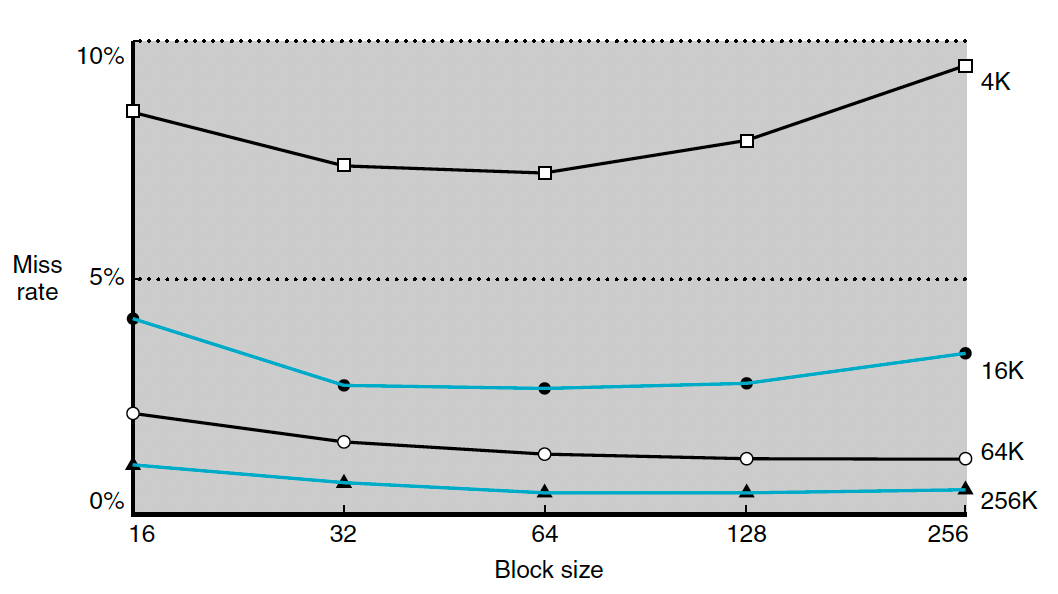
이 그림을 보면 블록의 크기가 너무 크면 오히려 miss rate가 늘어나게 된다. 왜냐하면 캐시 내의 블록개수가 너무 적어서 블록에 대한 경쟁이 심해지기 때문이다. 블록 내의 워드를 별로 사용하지 못했는데 그 블록이 캐시에서 쫒겨나게 되는 것이다. 심지어 실패 비용이 무지 비싸진다는 단점이 있다.

Handling cache misses(캐시 실패의 처리)

만약 cache miss가 일어나면 전체 파이프라인의 실행이 stall되고 메모리에서 word(data)를 가져와야한다.

1. Original PC value(PC - 4)값을 메모리에서 확인한다
2. 메모리에서 모든걸 다 읽을 때 까지 기다려야한다.
3. 메모리에서 가져온 데이터를 캐시 엔트리의 데이터 부분에 쓰고 tag와 valid bit까지 써서 캐시에 넣어준다.
4. Instruction을 다시 시작한다. 이때는 cache에서 miss가 아니라 hit이기 때문에 정상적으로 data를 얻을 수 있다.

Handling write(쓰기의 처리)

쓰기는 약간 다르게 작도한다. Store 명령어를 실행할 때 cache에만 저장했으면 memory와 서로 다른 값을 가지게 되는 문제가 생긴다. 그래서 두가지 방법을 통해 해결하게 된다.

• Write-through: 이 방식은 항상 데이터를 cache와 memory에 같이 쓰는 방식이다. 이 방식이 처리하기는 좋지만 좋은 성능을 보여주지는 않는다. 항상 메인 메모리에 데이터를 써야하기 때문에 성능이 굉장히 떨어진다. 그래서 write buffer를 쓰게 된다. 이것은 data가 memory에 저장되기 전에 buffer에 저장해두는 것이다.(Write buffer는 독립적으로 실행되어 천천히 memory에 저장시켜주게 된다.)
• Write-back: 이 방식은 cache에서 쫒겨날때 하위 메모리에 쓴 후 cache를 update하는 방식인데 문제는 실제로 구현하는데에는 복잡한다.

Main memory supporting caches

만약 DRAM을 메인 메모리로 사용하고 cache block read에서 address transfer에 1bus cycle, DRAM access에 15bus cycle, data transfer에 1bus cycle이 필요하다. 그때 4-word block, 1-word-wide DRAM을 사용한다면 miss penalty는 $1+4\times15+4\times1 =65$bus cycle이고 bandwidth는 16byte/65byte=0.25[B/cycle]이 된다.

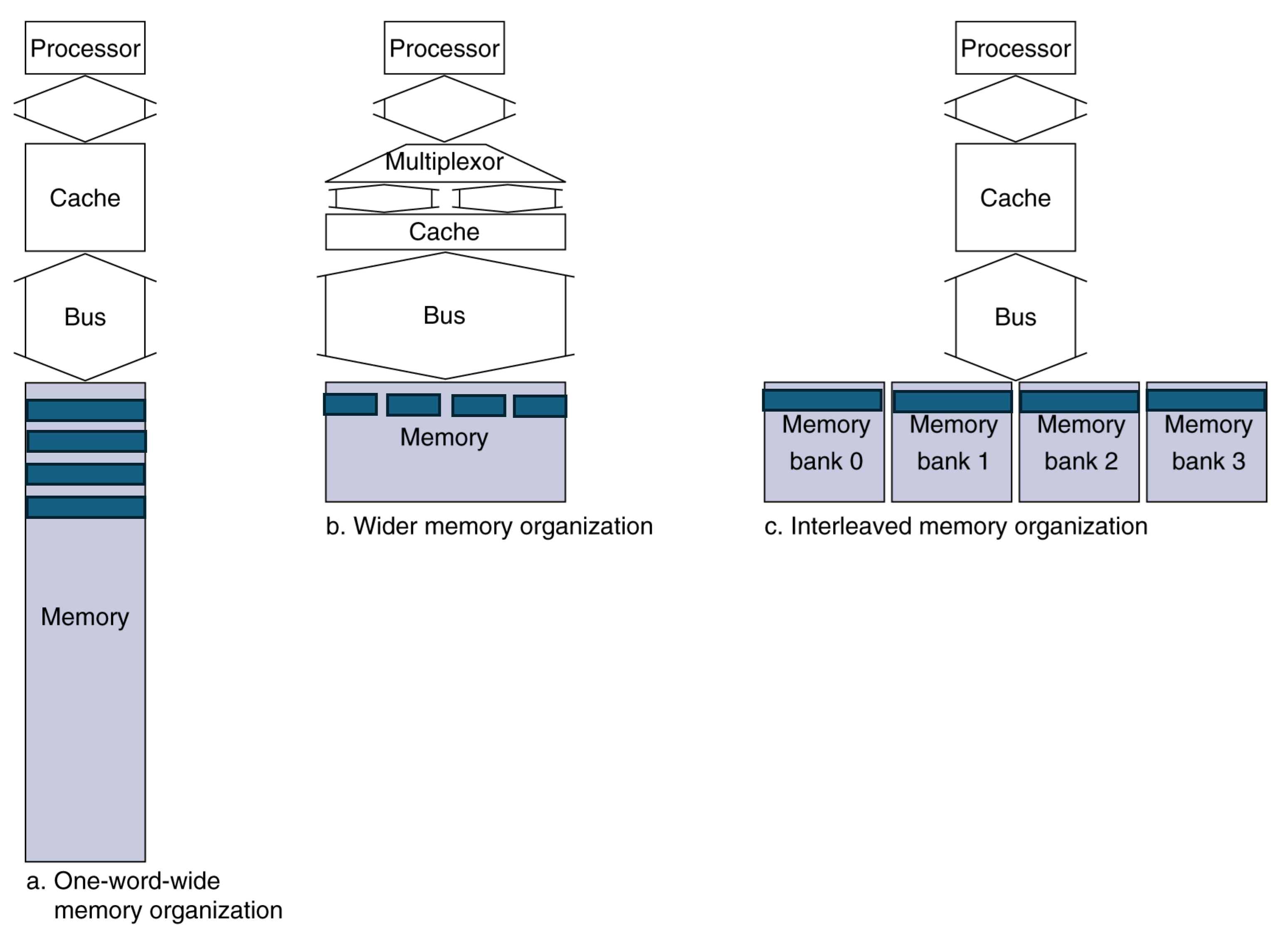
wide memory oranization의 경우 1+15+1=17 bus cylces가 되고 bandwidth는 16/17=0.94가 되고 interleaved memory의 경우 1+15+4$\times$1=20, 16/20=0.8이 된다.그래서 bandwidth를 늘리면 miss panalty를 줄일 수 있다.

이렇게 효율을 더 좋게 높이는 방법에는 메모리 폭을 넓히는 것과 interleaving을 사용하는 방법이 있다. Memory interleaving은 memory의 bank를 늘려서 각각이 독립적으로 작업하여 병렬적으로 실행되는 것이다.

◼︎ 캐시 성능의 측정 및 향상

캐시의 성능을 향상시키는데에는 두 가지 방법이 있다.

1. 2개의 다른 메모리 블록이 캐시의 같은 장소를 두고 경쟁하는 확률을 줄이는 방법
2. 메모리 계층구조에 새로운 계층을 추가하는 방법(Multilevel caching)

CPU time = (CPU execution clock cycle + Memory stall clock cycle) $\times$ Clock cycle time

Memory stall clock cycle = Read stall clock cycle + Write stall clock cycle

Read stall clock cycle = $\frac{\mathtt{Reads}}{\mathtt{Programs}}\times$ Read miss rate $\times$ Read miss penalty

Write stall clock cycle = $\frac{\mathtt{Writes}}{\mathtt{Programs}}\times$ Write miss rate $\times$ Write miss penalty + Write buffer stall (for write through)

보통은 read miss와 write miss의 값은 같다. 그래서 식을 다음과 같이 쓸 수 있다.

Memory stall clock cycle = $\frac{\mathtt{Instruction}}{\mathtt{Programs}}\times \frac{\mathtt{misses}}{\mathtt{Instruction}}\times$ Miss penalty

Example

Miss rates

• Instruction cache miss rate: 2%
• Data cache miss rate: 4%

Other conditions

• CPI: 2 without any memory stalls
• Miss penalty: 100 cycles for all misses,

How much faster a machine would run with a perfect cache that never missed

• Frequency of all loads and stores: 36%
• Calculate CPIs and compare them.

우선 Instruction miss cycle은 I $\times$ 2% $\times$ 100 = 2.00I이고 data miss cycle은 I $\times$ % $\times$ 36% $\times$ 100 = 1.44I이다. 그래서 총 miss cycle은 3.44I가 되는데 memory stall 없이 2CPI이므로 최종 CPI는 5.44I이다. 즉, 완벽한 캐시는 5.44I/2I=2.72배 더 좋다.

그런데 프로세서의 속도가 빨라지면 오히려 miss penalty를 마주할 가능성이 높아지게 된다. 그리고 clock rate와 CPI가 좋아지면 오히려 안좋아진다. CPI가 낮을수록 오히려 stall cycle에 피해를 크게 입게 되고 clock이 빨라질수록 같은 시간 안에 miss는 더 많이 나기 때문에 상대적으로 cache penalty가 늘어나는 현상이 일어나게 된다.

Fully associative cache

이는 direct mapped와 반대되는 방식이다. direct mapped는 메모리 블록 주소를 상위 계측 한 주소에 1대1 대응되게 한다. 하지만 fully associative방식은 블록이 캐시 내의 어느곳에나 들어갈 수 있는 방식이다. 이 방식의 단점은 어떤 data를 찾기 위해선 모든 엔트리를 검색해야한다. 그래서 보통 비교기를 병렬적으로 사용한다. 이는 하드웨어 비용이 커지므로 작은 캐시에서만 쓸 수 있다.

Set associative cache

이는 direct mapped와 fully associative 방식의 중간정도라고 생각할 수 있다. 이 방식에서는 한 블록이 들어갈 수 있는 자리의 개수가 고정돼(fixed)있다.

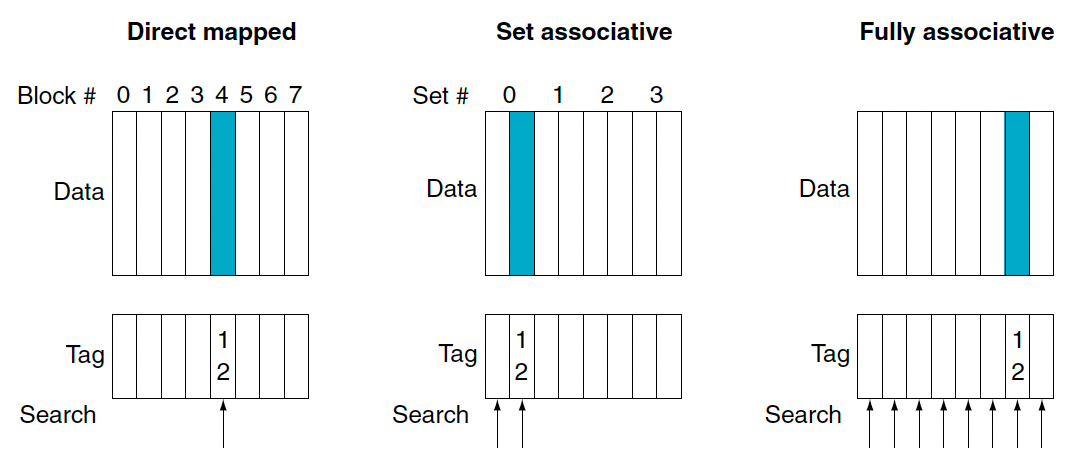
Set associative 방식은 그래서 블록당 n개의 배치 가능한 위치로 나누게 된다. 각 집합 내에서는 아무 장소나 들어갈 수 있다. 그래서 위의 경우는 n이 4인 set associative cache를 보여주고 있다.

• Direct mapped cache: (Block number) modulo (Number of cache blocks)
• Set associative cache: (Block number) modulo (Number of sets in the cache)

그래서 위의 예시에서 주소가 12인 블록에서는 direct mapped 방식에서는 (12 modulo 8) = 4이고 set associative 방식에서는 (12 modulo 4) = 0번 집합에 아무곳이나 들어간 것이다. Fully associative는 그냥 랜덤하게 들어가게 된다.

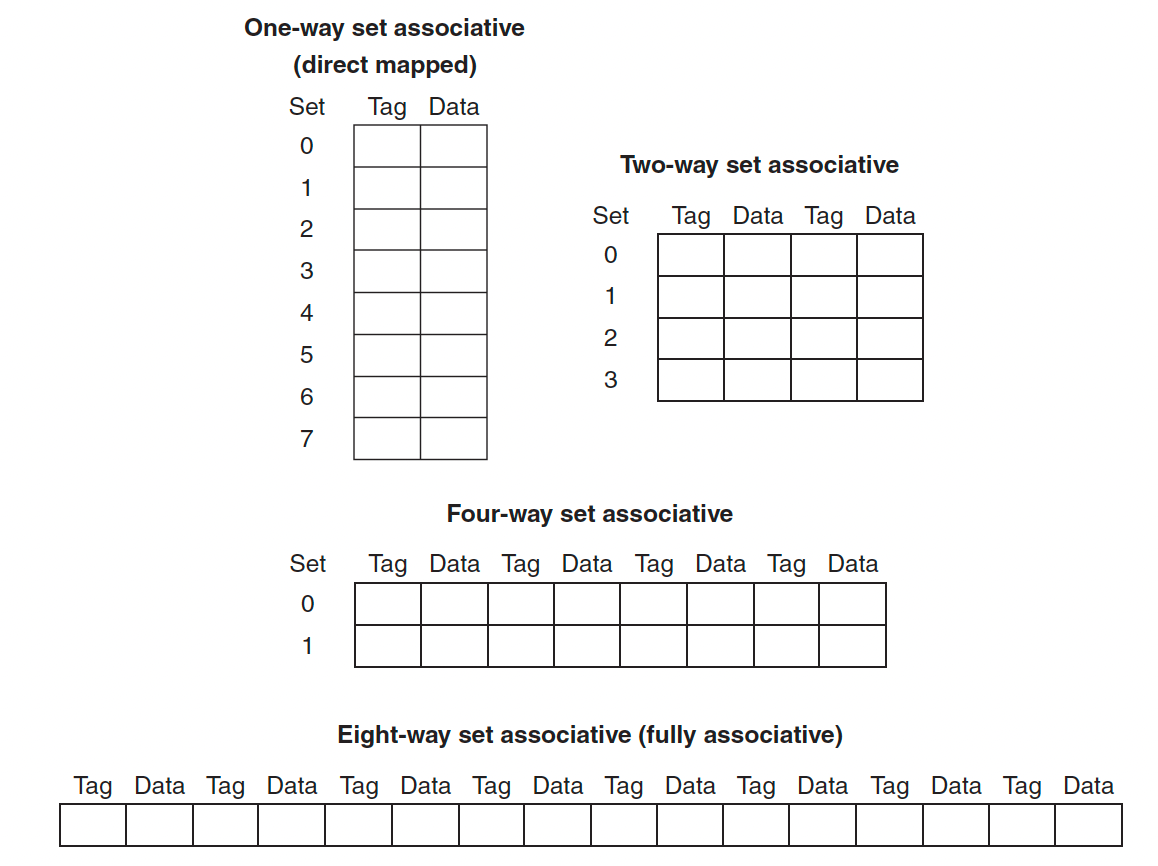
전체 블록 수는 집합의 수와 associativity를 곱한 값과 같다. 그래서 associativity가 늘어나면 miss rate가 줄어들지만 검색하는데에 시간 때문에 hit time자체는 늘어나게 된다.

Example

블록이 4개고 주소 0, 8, 0, 6, 8 순으로 브록을 참조할 때 direct mapped, 2-way set associative, fully associative 방식에서 hit과 miss를 판별하여라. 다음은 direct mapped 방식을 상용했을 때 이다.

Block address	Cache block
0	(0 modulo 4) = 0
6	(6 modulo 4) = 2
8	(8 modulo 4) = 0

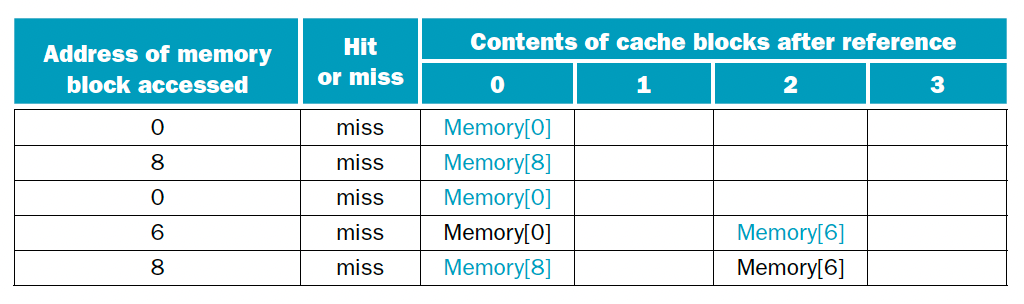
이때는 5번의 접근 시도에 다섯 번의 실패가 발생했다. 다음은 2-way set associative 방식이다.

Block address	Cache block
0	(0 modulo 2) = 0
6	(6 modulo 2) = 0
8	(8 modulo 2) = 0

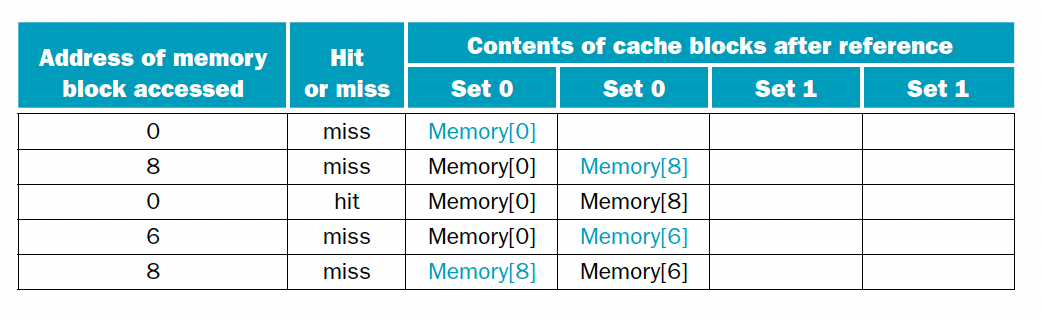
이때는 5번의 시도중 한번의 hit가 발생한다. 마지막으로 fully associative 방식을 택하면 다음과 같다.

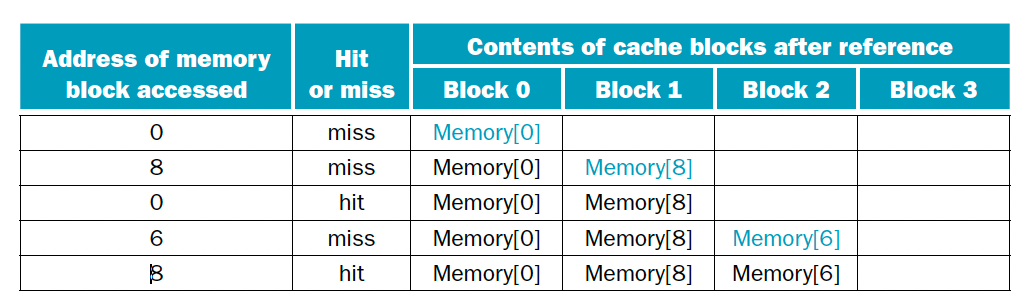
이때는 5번의 시도중 2번의 hit가 되기떄문에 제일 성능이 좋다.

◼︎ Block replacement policy

Valid value가 0이면 miss이기 때문에 보통은 그 비어있는 index에서 첫번째 빈 위치에 쓰게 되는데 만약 이 공간이 다 차있으면 replace를 해 줘야한다. 그래서 block replacement policy가 필요한 것이다.

LRU (Least Recently Used)

이 방식은 가장 오랫동안 사용되지 않은 블록이 교체되는 방식이다. 그래서 각 data가 언제 쓰였는지를 기억하고 있어야한다. Temporal locality에 의해 최근 사용된 것은 또 사용될 가능성이 높기 때문에 안쓴지 오래된 것을 바꾸는 방식은 효과적이다. 하지만 이 언제 쓰였는지 기억하는 시스템 자체를 구현하는 것이 복잡한다. 왜냐하면 2way이면 one bit의 LRU 가 필요하지만 4way나 그 이상이면 하드웨어가 복잡해져야하기 때문이다.

Example

먄약 2-way set associative방식이고 0, 2, 0, 1 , 4, 0, 2, 3, 5, 4순서로 주소를 사용한 결과는 어떻게 될까?

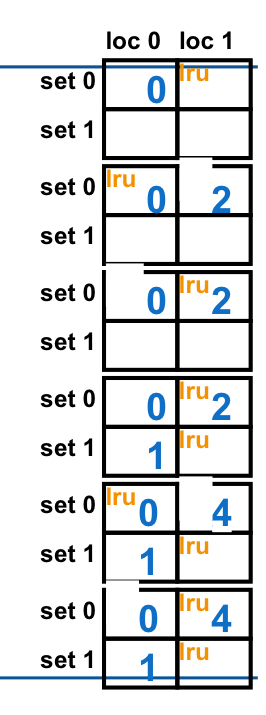
이런식으로 점점 쓰면 된다.

◼︎ Performance of multilevel cache

Perfect cache일 때는 CPI가 1.0이고 clock rate는 4GHz, main memory access time은 100ns이고 primary cache의 miss rate는 2% 이고 0.5%의 miss rate를 가지고 access time이 5ns인 secondary cache를 추가하면 total CPI가 어떻게 될까?

• L1 cache만 있을 때: 1 + 100ns * 4GHz * 0.02 = 8
• L1, L2 cache 사용할 때: 1 + 5ns * 4Ghz * 0.02 + 100ns * 4Ghz * 0.005 = 1 + 0.4 + 2.0 = 3.4

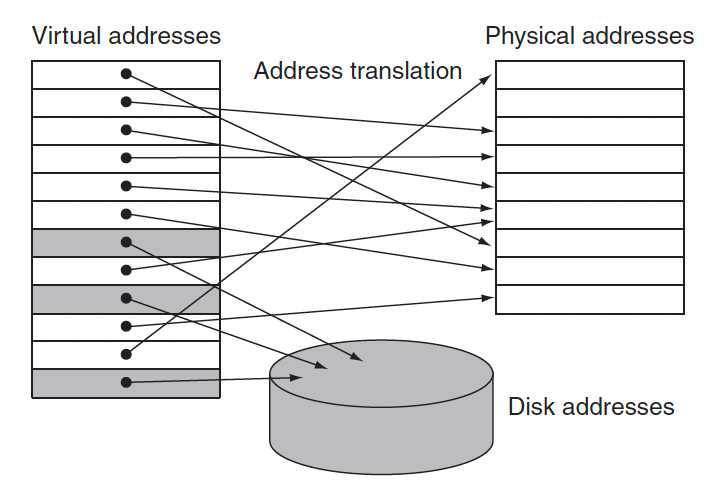
◼︎ Virtual memory

가상 메모리는 main memory를 secondary storage를 위한 cache로 생각하는 기술이다. 실제 물리적 크기에 비해 더 크게 사용하는 방법이다. Virtual address를 통해 가상의 저장 공간이 있다고 만드는 것이고 이 프로그램은 virtal address를 physical address로 변환하는 역할을 한다.