CA - chapter 3 Arithmetic for Computers

이번장에서는 컴퓨터가 계산하는 방식에 대해 볼것이다. Addition, subtraction, multiplication, overflow에 대해 다뤄볼 것이다. Division이나 floating point같은 것도 있긴 하지만 교수님은 이부분을 크게 다루시지 않아서 넘기겠다.

◼︎ 덧셈과 뺄셈

덧셈 같은 경우는 그냥 이진수 계산을 하면 된다. 1+1이면 0으로 되면서 carry를 왼쪽으로 옮겨주면 된다. 그런데 뺄셈이 문제이다. 컴퓨터는 덧셈을 이용하여 뺄셈을 한다. 바로 보수를 구해서 더해주면 된다.

$A - B = A + (-B) = A + \bar{B}$

Overflow

양수와 양수를 더했는데 음수가 나올때가 있다. 그러면 오버플로우가 일어났다는 것이다.

Arithmetic Logic Unit(ALU) Design

ALU: the device that performs the arithmetic operation or logical operation

기본적인 ALU는 AND & OR logical unit과 full adder를 합쳐서 만든다.

1-Bit logical unit

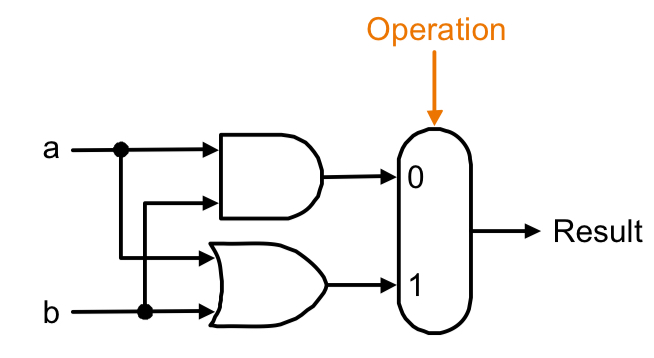
1-Bit full adder

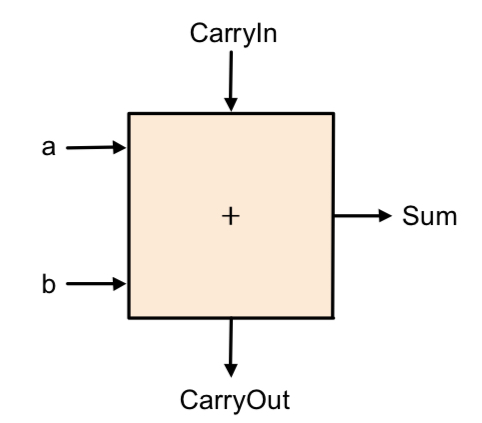
1-Bit ALU

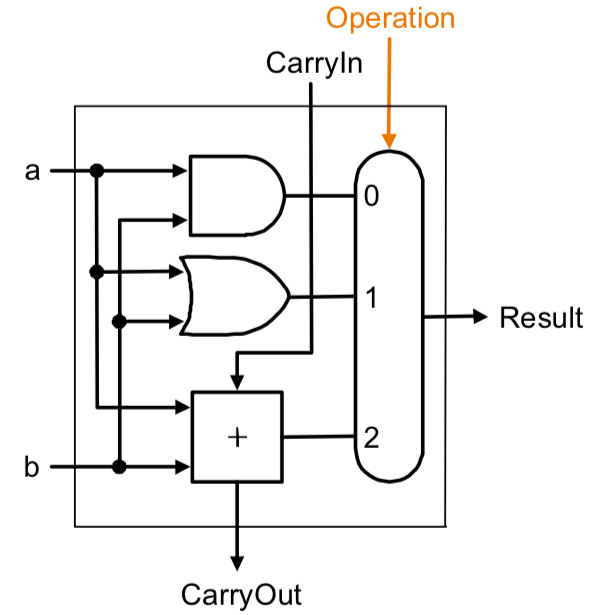
Operation 부분은 MUX로 0이면 AND, 1이면 OR, 2면 ADD연산을 result로 선택하게 된다.

32-Bit ALU

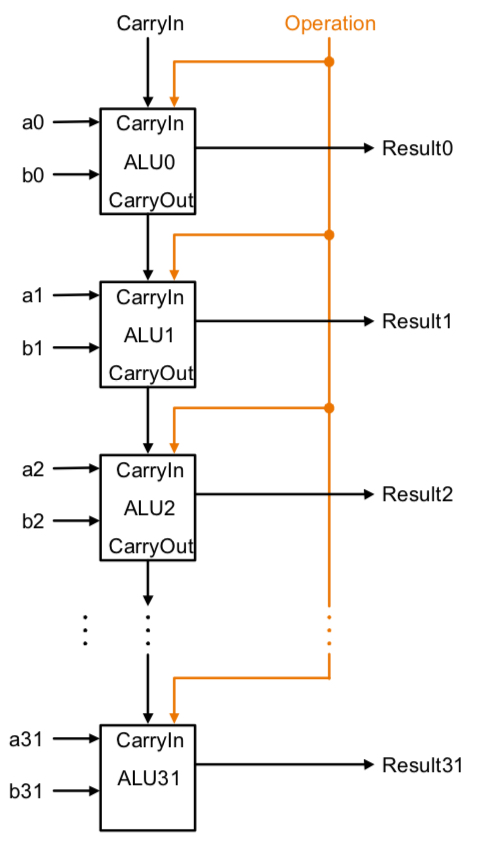
이렇게 이전 자리의 carry out을 현재 자리의 carry in과 연결시키고 result의 순서대로 이어붙이면 32bit 크기의 ALU가 완성된다.

1-Bit subtraction

뺄셈의 경우에는 adder에 조금 변형을 주면 사용할 수 있게 된다.

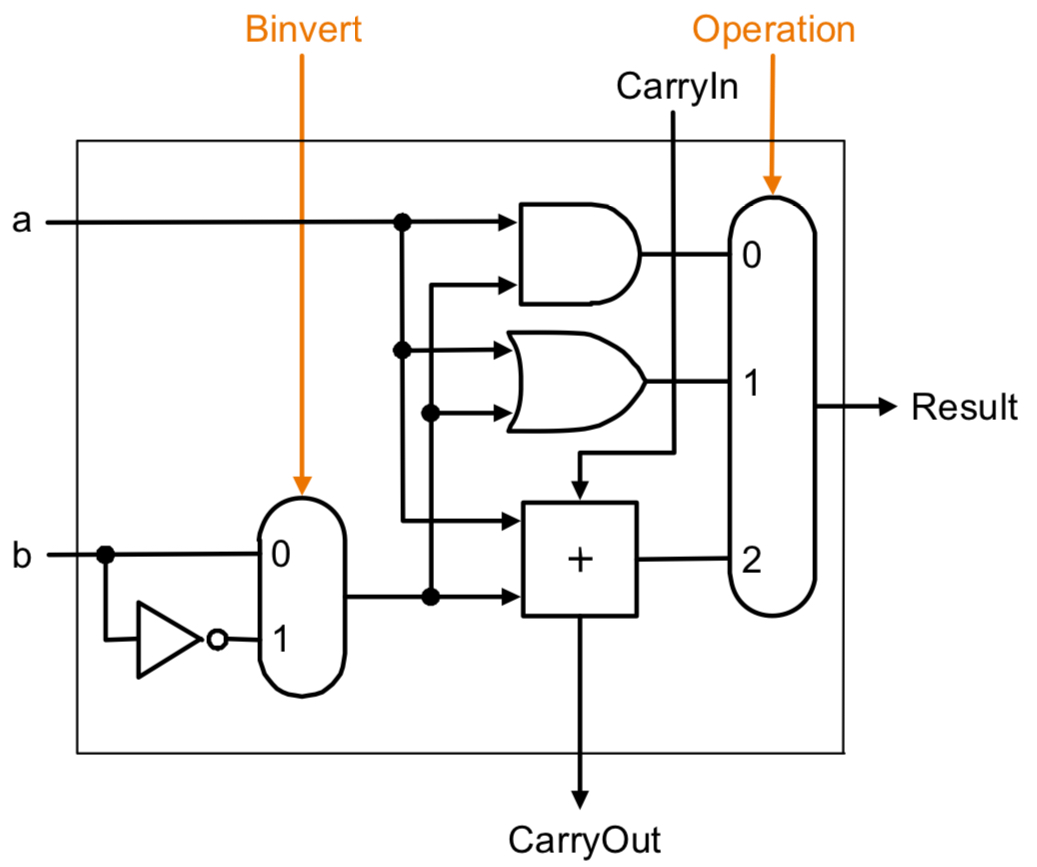
Binvert의 Mux에 0이 들어가면 +를 계산하고 1이 들어가면 -를 계산하게 되는 것이다.

4-Bit Adder Subtractor

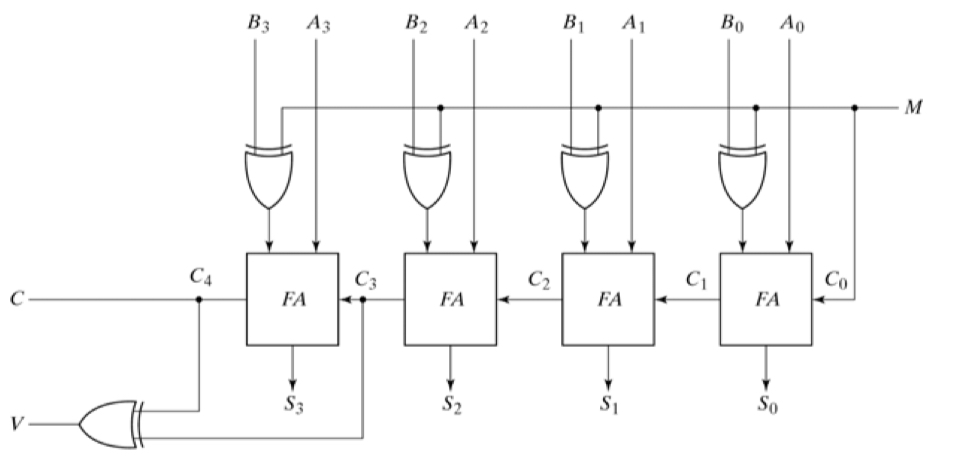
◼︎ 곱셈(Multiplication)

• Multiplicand (피승수): 곱해지는 수 → 첫 번째 피연산자(First operand)
• Multiplier (승수): 곱하는 수 → 두 번째 피연산자(Second operand)
• Product (곱셈 결과): 결과값(Result)

multiplicand가 n-bit이고 multiplier가 m-bit이면 product의 최대 비트 크기는 n+m이다.

Example

     1011     (multiplicand, 11 in decimal)
×    1001     (multiplier,   9 in decimal)
----------
     1011     (1011 × 1)
    0000      (1011 × 0, shift left by 1)
   0000       (1011 × 0, shift left by 2)
  1011        (1011 × 1, shift left by 3)
----------
  1100011     (binary result) = 99 in decimal

1이면 복사 0이면 0으로 다 채우면 되고 하나씩 옆으로 옮기면 되는 것이다.

First version of the multiplication

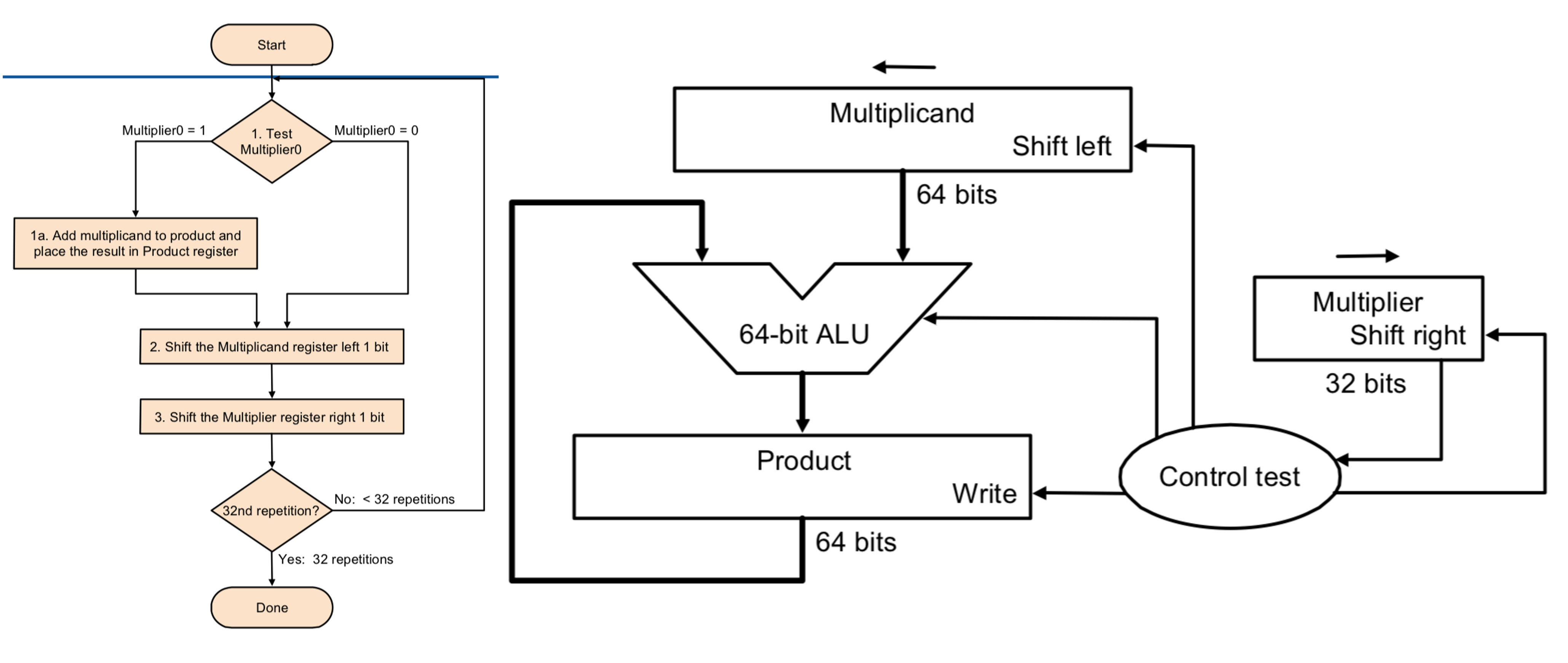
이 그림은 초기의 곱셈 알고리즘과 하드웨어 구조이다. 이대로 계산하면 다음과 같다.

000001011
×       1
----------
000001011 ... (1)

000010110
×       0
----------
000000000 ... (2)

000101100
×       0
----------
000000000 ... (3)

001011000
×       1
----------
001011000 ... (4)

(1) + (2) + (3) + (4) =
  000001011
  000000000
  000000000
+ 001011000
----------
  001100011

이것은 4bit짜리의 multiplication을 한 것이다. 여기서 보면 왜 위에 그림에서 32bit의 계산을 할때 multiplier는 32bit인데에 반해 multiplicand가 64bit고 product가 64bit인지를 이해할 수 있다.

Refined version of multiplication

그런데 딱봐도 이건 0을 넣어주기위한 불필요한 추가 bit(memory)와 연산이 많은게 보이지 않는가? 그래서 이것을 보완한 방법을 구현했다.

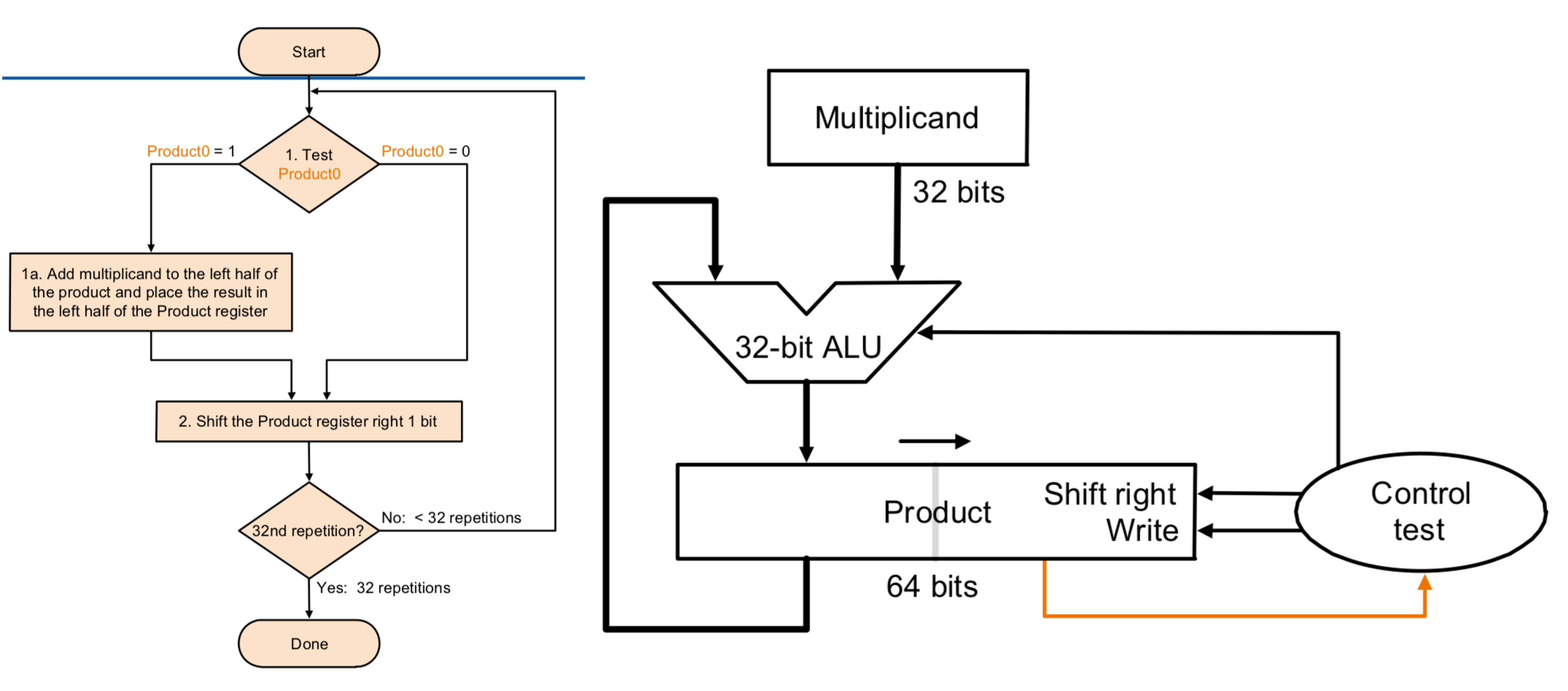
이러면 64bit였던 multiplicand를 32bit로 줄일 수 있다. 이 방법은 multiplicand를 product앞의 32bit에 더해주거나 안더해주는 방식으로 한다. 예시를 통해 해보겠다.

multiplicand: 1011
multiplier: 1001

(1)
product: 0000 1001 (앞 4bit는 일단은 0 뒤에 비트는 multiplier)

(2)
product: 1011 1001 (multiplier[0] = 1이면 multiplicand 더하기)
product: 0101 1100 (>>)

(3)
product: 0010 1110 (>>, multiplier[0] = 0이면 >>)

(4)
product: 0001 0111 (>>)

(5)
product: 1100 0111 (multiplier[0] = 1이면 multiplicand 더하기)
product: 0110 0011 (>>)

result: 0110 0011 = 99